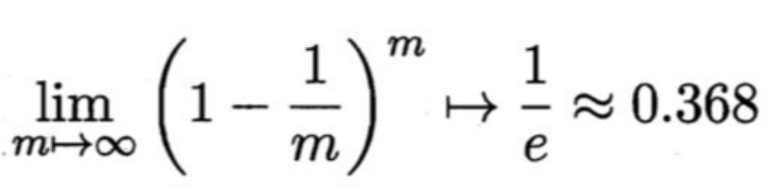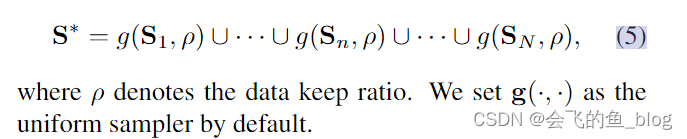文章目录
- 前言
- 问题引出
- open-set问题
- 抛出
- 解决方法
- softmax函数、softmax-loss函数
- 解决
- 代码(center_loss.py)
- 原理
- 程序解释
- 代码运用
- 如何梯度更新
- 首先了解一下基本的梯度下降算法
- 然后
- 代码解释见下面train()
- 补充:外围知识(models.py)
- 卷积神经网络(cnn)
- 神经网络模型搭建(单层神经网络)
- 补:nn.ReLU()与F.relu()的区别
- 卷积神经网络的提出
- 论文中的阐述
- 代码解释
- 补充:(datasets.py)
- 代码解释
- 代码运用
- transforms.py
- 补充:(utils.py)
- 代码解释
- 代码应用
- main.py解释
- argparse模块应用
- 代码解释
- plot_features()函数
- matplotlib模块应用
- 代码解释
- 代码运用
- train()
- nn.CrossEntropyLoss()
- 一般更新步骤
- 简单例子
- 代码解释
- test()
- 一般测试步骤
- 代码解释
- main()
- 参数
- torch.optim.SGD
- STEPLR
- main()代码解释
- 总结
前言
学习一下: 中心损失函数,用于用于深度人脸识别的特征判别方法
论文:https://ydwen.github.io/papers/WenECCV16.pdf
github代码:https://github.com/KaiyangZhou/pytorch-center-loss
参考:史上最全MNIST系列(三)——Centerloss在MNIST上的Pytorch实现(可视化)
问题引出
open-set问题
open-set 问题是一种模式识别中的问题,它指的是当训练集和测试集的类别不完全相同的情况。例如,如果训练集只包含 0 到 9 的数字,而测试集包含了 A 到 Z 的字母,那么就是一个 open-set 问题。这种情况下,分类器不仅要正确识别已知的类别,还要能够拒绝未知的类别,即将它们标记为 unknown 或 outlier。(后来我想这就是一个聚类问题)
open-set 问题与 closed-set 问题相对应,closed-set 问题是指训练集和测试集的类别完全相同的情况。例如,如果训练集和测试集都只包含 0 到 9 的数字,那么就是一个 closed-set 问题。这种情况下,分类器只需要正确识别已知的类别即可。
抛出
当我们要预测的人脸不在训练集中出现过时,我们需要让它不识别出,而不要因为与训练过的人脸相像而误判。
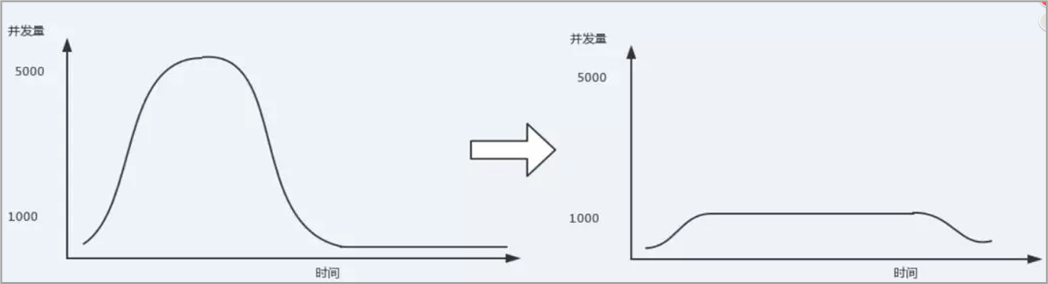
对于常见的图像分类问题,我们常常用softmax loss来求损失。以MNIST数据集为例,如果你的损失采用softmax loss,那么最后各个类别学出来的特征分布大概如下图:(在倒数第二层全连接层输出了一个2维的特征向量)
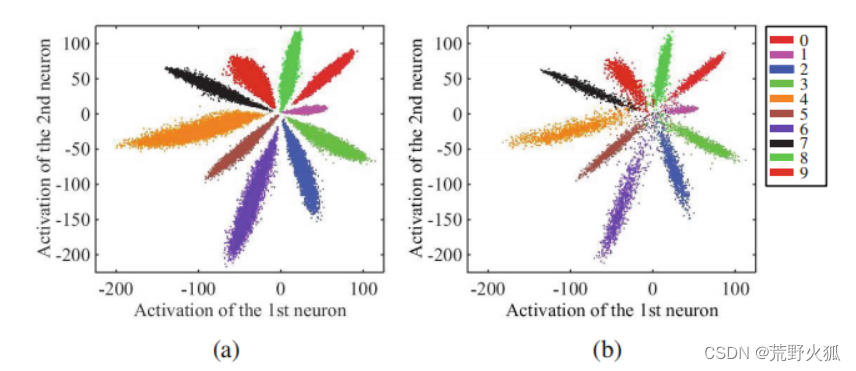
左图为训练集,右图为测试集,发现结果分类还算不错,但是每一类的界限太过模糊,若从中再加一列,则有可能出现误判。
解决方法
softmax函数、softmax-loss函数
已知softmax的函数为:
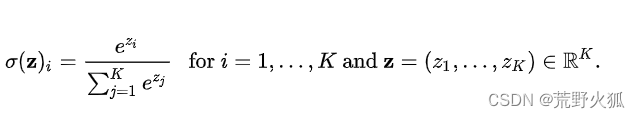
在深度学习的分类问题上,意为对应类的概率(符合每个类的概率相加和为1且0<每个类的概率<1)。(输出层后的结果)
其中 zi 是第 i 个输出节点的值,K是输出节点的个数,即分类的类别数。softmax函数的作用是将输出节点的值归一化为范围在 [0, 1] 且和为 1 的概率值,表示属于每个类别的可能性。
softmax的损失函数:(具体详见:一文详解Softmax函数)(也叫交叉熵损失)
在softmax的函数的基础上,我们要求正确对应类的概率最大,

即,损失函数为:(越小越好)

其中z = wTx+b,m是小批量的样本的个数,n是类别个数,w是全连接层的权重,b为偏置项,(一般来说w,b是要学习出来的),xi是第i个深层特征,属于第yi类。

解决
在分类的基础上,我们还要求,每个类,往自己的中心的特征靠拢,使类内间距减少,这样才能更加显出差别。
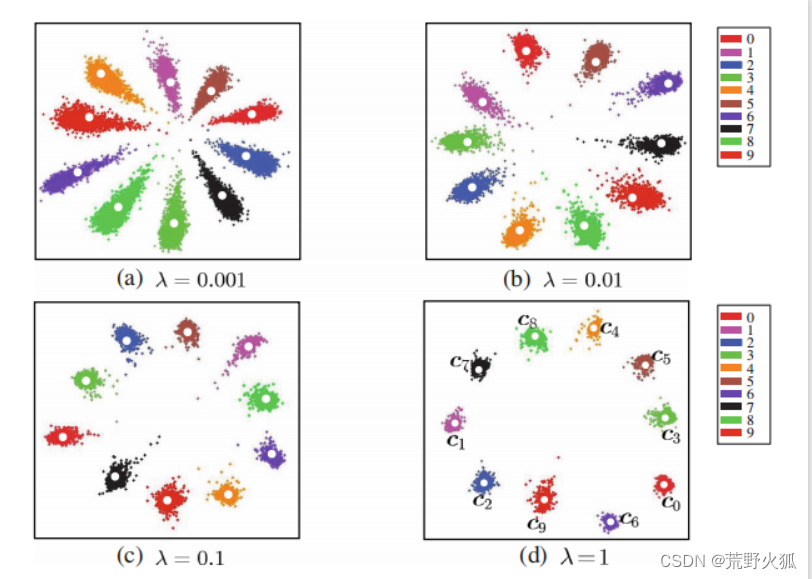
于是,论文作者提出如下新的损失函数:
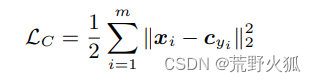
其中 xi 是第 i 个样本的特征向量,cyi 是第 yi 个类别的中心向量,m 是样本的个数。
小的注意点:这里用的是样本数,也就是说,是在小批量分类任务完成后再进行的聚类任务
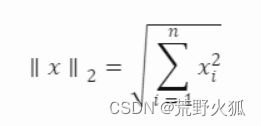
我们不难发现,作者这里用的是欧式距离的平方,即在多维空间上的两点之间真实距离的平方。
实际上,我们很容易发现,这实际上是一个聚类问题,常见的聚类问题上用的是误差平方和(SSE)损失函数:
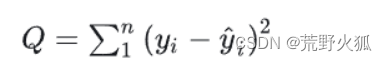
论文作者仅从此推出的欧式距离的平方,仅从形式上十分相像,当然可以作为此聚类问题的解决。
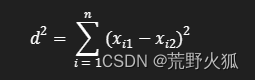
(在二维上,可以简单看成是直角三角形斜边的平方=两直角边平方和)
为何要加以平方:欧式距离的平方相比欧式距离有一些优点,例如:
1、计算更快,省去了开方的运算。
2、更加敏感,能够放大距离的差异,使得离群点更容易被发现。
3、更加方便,能够与其他平方项相结合,如方差、协方差等。
最后,作者沿用softmax损失函数与中心损失函数相加的方法(在损失函数上很常见),
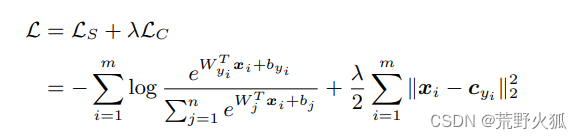
这里的1/2很容易想到是作为梯度下降时与后面的平方用来抵消的项,这里λ 可以看作调节两者损失函数的比例
来作为总体的损失函数,作为此问题的解决。
代码(center_loss.py)
原理
首先确定三个事实:
1、在之前的学习中通过实践得知(最小二乘法那块),在拟合的最后结果上,在利用SSE损失函数与MSE损失函数作为损失值参与到程序中时,拟合出的结果并无差别,只有在结果出来后,作为评判模型的好坏时,才有数值上的差别。(两者区别在于是否求平均)。
2、1/2的乘或不乘,只对运算的过程的简便程度有影响,与结果无影响。
3、图像是二维的。
于是我们将作者的的中心损失函数稍加变形。就得到了如下形式(事实上,github上给出的代码就是这么写的)

程序解释
参考:Center loss-pytorch代码详解
这里只做补充:
import torch
import torch.nn as nn
class CenterLoss(nn.Module):
"""Center loss.
# 参考
Reference:
Wen et al. A Discriminative Feature Learning Approach for Deep Face Recognition. ECCV 2016.
# 参数
Args:
num_classes (int): number of classes. # 类别数
feat_dim (int): feature dimension. # 特征维度
"""
# 初始化 默认参数:类别数为10 特征维度为2 使用GPU
def __init__(self, num_classes=10, feat_dim=2, use_gpu=True):
super(CenterLoss, self).__init__() # 继承父类的所有属性
self.num_classes = num_classes
self.feat_dim = feat_dim
self.use_gpu = use_gpu
if self.use_gpu: # 如果使用GPU
#nn.Parameter()将一个不可训练的tensor转换成可以训练的类型parameter,并将这个parameter绑定到一个module里面,参与到模型的训练和优化中。
#nn.Parameter的对象的requires_grad属性的默认值是True,即是可被训练的,这与torth.Tensor对象的默认值相反。
self.centers = nn.Parameter(torch.randn(self.num_classes, self.feat_dim).cuda())
# 初始化中心矩阵 .cuda()表示将数据放到GPU上
else:
self.centers = nn.Parameter(torch.randn(self.num_classes, self.feat_dim))
def forward(self, x, labels): # 前向传播
"""
Args:
x: feature matrix with shape (batch_size, feat_dim). # 特征矩阵
labels: ground truth labels with shape (batch_size). # 真实标签
"""
batch_size = x.size(0) #batch_size x的形式为tensor张量
# .pow对x中的每一个元素求平方 dim=1表示按行求和 keepdim=True表示保持原来的维度 expand是扩展维度
distmat = torch.pow(x, 2).sum(dim=1, keepdim=True).expand(batch_size, self.num_classes) + \
torch.pow(self.centers, 2).sum(dim=1, keepdim=True).expand(self.num_classes, batch_size).t() #.t()表示转置 均转成batch_size x num_classes的形式
# .addmm_()表示进行1*distmat + (-2)*x@self.centers.t()的运算 @表示矩阵乘法
distmat.addmm_(1, -2, x, self.centers.t())
classes = torch.arange(self.num_classes).long()# 生成一个从0到num_classes-1的整数序列 long表示数据类型
if self.use_gpu: classes = classes.cuda()
#这里 .unsqueeze(0) 例[0,4,2] -> [[0,4,2]] .unsqueeze(1) 例[0,4,2] -> [[0],[4],[2]]
labels = labels.unsqueeze(1).expand(batch_size, self.num_classes)# .unsqueeze(1)表示在第1维增加一个维度 .expand()表示扩展维度
mask = labels.eq(classes.expand(batch_size, self.num_classes)) #eq是比较两个tensor是否相等,相等返回1,不相等返回0
# *表示对应元素相乘
dist = distmat * mask.float() # mask.float()将mask转换为float类型
loss = dist.clamp(min=1e-12, max=1e+12).sum() / batch_size # clamp表示将dist中的元素限制在1e-12和1e+12之间
return loss
代码运用
import torch
import torch.nn as nn
from center_loss import CenterLoss
criterion_cent =CenterLoss(10, 2,False) #10个类别,2维
torch.manual_seed(0) #设置随机种子
x = torch.randn(10, 2) # (32, 2) #32个样本,每个样本2维
labels = torch.randint(0, 10, (10,)) # (32,) #32个样本,每个样本一个标签
print(x)
print(labels)
print(criterion_cent(x, labels))
结果:
tensor([[-1.1258, -1.1524],
[-0.2506, -0.4339],
[ 0.5988, -1.5551],
[-0.3414, 1.8530],
[ 0.4681, -0.1577],
[ 1.4437, 0.2660],
[ 1.3894, 1.5863],
[ 0.9463, -0.8437],
[ 0.9318, 1.2590],
[ 2.0050, 0.0537]])
tensor([2, 9, 1, 8, 8, 3, 6, 9, 1, 7])
tensor(2.9281, grad_fn=<DivBackward0>)
如何梯度更新
首先了解一下基本的梯度下降算法
【点云、图像】学习中 常见的数学知识及其中的关系与python实战
里的小标题:基于迭代的梯度下降算法,了解到超参数(人为设定的参数):
学习率,w,b等。此算法为拟合出一条线。
伪代码:
1、未达到设定迭代次数
2、迭代次数epoch+1
3、计算损失值
4、计算梯度
5、更新w、b
6、达到迭代次数,结束
然后
看下这里的更新方法

其中,卷积层中初始化的参数 θc,超参数 :λ、α 和学习率 μ ,迭代次数 t 。(λ、α、 μ均可调)
伪代码:
1、当未收敛时:
2、迭代次数t+1
3、计算损失函数 L=Ls+Lc
4、计算反向传播误差(即梯度)
5、更新w
6、更新cj
7、更新θc
8、结束
其中
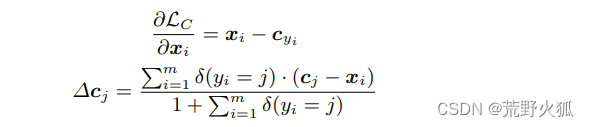
其中,如果满足条件,则 δ(条件) = 1,如果不满足,则 δ(条件) = 0。
首先:第一个公式不用多说,为中心损失函数对特征xi求偏导,即求梯度。
其次:第二个公式:加入了判断,当条件满足时(即yi=j,即就是在同一类时)Δcj=cj-xi 的小批量的所有和/m+1。相当于累加了误差求平均,以此来作为梯度。(分母上的累加和看着恐怖,实际上就是m个1相加。)
当条件不满足时,即Δcj =0,此时这个分母的+1的作用就体现出来了,分母不能为0嘛。
补充:
第5步后面一个等号成立是因为Lc中没有W项,所以Lc对W的求导为0
第7步也是一样,求梯度,只是写成了求导的链式法则。
代码解释见下面train()
梯度更新代码
for epoch in range(args.max_epoch): #
print("==> Epoch {}/{}".format(epoch+1, args.max_epoch))
train(model, criterion_xent, criterion_cent,
optimizer_model, optimizer_centloss,
trainloader, use_gpu, dataset.num_classes, epoch)
if args.stepsize > 0: scheduler.step()
if args.eval_freq > 0 and (epoch+1) % args.eval_freq == 0 or (epoch+1) == args.max_epoch:
print("==> Test")
acc, err = test(model, testloader, use_gpu, dataset.num_classes, epoch)
print("Accuracy (%): {}\t Error rate (%): {}".format(acc, err))
补充:外围知识(models.py)
卷积神经网络(cnn)
参考:
1、CNN笔记:通俗理解卷积神经网络
2、wiki卷积神经网络
3、pytorch官方CONV2D
补充:
1、五种经典卷积神经网络
大前提:输入的x为tensor张量
(样本数x通道数x高x宽)torch.randn(3, 3, 10, 10)
(实际上就是多维数组,不用pytorch的话,numpy数组也能实现,两者很多有共通之处)
神经网络模型搭建(单层神经网络)
得出以下已知:
先从nn(神经网络)讲起:
1、输入层->中间层->输出层 (中间层也叫隐藏层)
中间层只有一层时:我们可以做一个最简单的单层神经网络,也叫做单隐层感知机(single hidden layer perceptron)。
以下以单层神经网络为例,
借用此图:layer1:输入层,layer2:中间层,layer3:输出层。

而中间的线段,我们称之为线性层。上图就有两层线性层。
其中:中间线性层的计算公式为:y = WTx+b ,W为权重矩阵,b为偏置向量。函数为nn.Linear(in_features, out_features, bias=True) (这里为什么有转置,在下面main()里会讲)
也常用作作为分类器的最后一层,输出类别的概率或得分,这个时候我们可以看到它常见的名字叫全连接层。
简单运用一下:
import torch
import torch.nn as nn
linear = nn.Linear(10, 5) # 创建一个线性变换层,输入维度为 10,输出维度为 5
torch.manual_seed(0)#设置随机种子
input = torch.randn(3, 10) # 创建一个形状为 (3, 10) 的随机张量 3个特征,每个特征为10维 torch.randn返回一个张量,包含了从标准正态分布(均值为0,方差为 1)中抽取的一组随机数
output = linear(input) # 对输入张量进行线性变换
print(output.shape) # 输出张量的形状为 (3, 5)
print(output)
'''
torch.Size([3, 5])
tensor([[ 0.3224, 0.5811, -1.6699, 0.7644, 0.6194],
[-0.0365, -0.2294, 0.0931, -0.6751, -0.0490],
[ 0.2874, 0.7715, -0.4043, 0.3233, 0.0094]],
grad_fn=<AddmmBackward0>)
'''
2、激活函数的引入
激活函数的作用是为神经网络引入非线性因素,使得神经网络可以拟合复杂的函数,解决非线性的问题。
如果不使用激活函数,每一层的输出都是上一层输入的线性函数,无论神经网络有多少层,最终的输出都是输入的线性组合,这样的神经网络就失去了表达能力和泛化能力。
激活函数可以将线性变换后的值映射到一个特定的范围,比如 [0,1] 或者 [-1,1],这样可以限制输出值的幅度,防止梯度消失或爆炸。激活函数还可以增加神经网络的稀疏性,使得部分神经元的输出为零,从而减少计算量和过拟合。
常用的激活函数有 sigmoid、tanh、ReLU、Leaky ReLU、ELU、PReLU、Swish 等,它们各有优缺点,需要根据具体的问题和数据选择合适的激活函数。
于是,操作变成了如下:
输入层->中间层->输出层 。这个层数不变。
中间的过程为:输入层->全连接层->激活函数->中间层->全连接层->激活函数->输出层
代码:
# 导入 pytorch 库
import torch
import torch.nn as nn
import torch.nn.functional as F
# 定义网络结构
class SingleHiddenLayerPerceptron(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(SingleHiddenLayerPerceptron, self).__init__()
# 第一层是线性层,输入维度为 input_size,输出维度为 hidden_size
self.linear1 = nn.Linear(input_size, hidden_size)
# 第二层是线性层,输入维度为 hidden_size,输出维度为 output_size
self.linear2 = nn.Linear(hidden_size, output_size)
def forward(self, x):
# 前向传播,先经过第一层的线性变换和激活函数
x = F.relu(self.linear1(x))
# 再经过第二层的线性变换和激活函数
x = F.sigmoid(self.linear2(x))
# 返回输出
return x
# 创建一个输入维度为 10,隐藏层维度为 20,输出维度为 2 的网络
model = SingleHiddenLayerPerceptron(10, 20, 2)
print(model)
# 运用网络进行前向传播
torch.manual_seed(0)#设置随机种子
input = torch.randn(1, 10)
output = model(input)
print(output)
'''
SingleHiddenLayerPerceptron(
(linear1): Linear(in_features=10, out_features=20, bias=True)
(linear2): Linear(in_features=20, out_features=2, bias=True)
)
tensor([[0.5418, 0.5528]], grad_fn=<SigmoidBackward0>)
'''
若中间层为两层的神经网络可以依次递推。
一般来说神经网络的输入为1维(数组)。
输入可以改为:
input = torch.randn(3, 3, 10, 10) # (3, 3, 10, 10) #3个样本,3个通道,每个通道10x10
补:nn.ReLU()与F.relu()的区别
nn.ReLU()是一个类,它继承自nn.Module,可以作为一个网络的组件,需要指定输入维度和输出维度。它的作用是对输入张量进行逐元素的ReLU激活函数,即 y = max(0, x)。
F.relu()是一个函数,它属于torch.nn.functional模块,可以直接对输入张量进行操作,不需要创建对象。它的作用和nn.ReLU()相同,但是它还可以指定一个inplace参数,表示是否在原地修改输入张量,节省内存。
一般来说,nn.ReLU()用于定义网络结构的时候,F.relu()用于前向传播的时候。当用print(net)输出网络结构时,会有nn.ReLU()层,而F.relu()是没有输出的。
类似的:
F.max_pool2d(x, 2)与nn.MaxPool2d(2, 2)也是相同的区别
卷积神经网络的提出
后发现,
1、以上方法在针对同一张图旋转,缩放后的图的识别效果不好,于是想出提取图的局部特征。
2、全连接层在图片像素过大时,如100x100的图,权重过多为10000,训练时间会过长,而卷积神经网络的核大小,例如是5x5,则权重缩小为25,且能共享权重参数(即权重参数不变)。
为解决此方法,卷积神经应运而生。
出现的新名词:
1、卷积核: 若是3通道的图,核为3,则卷积核的大小为3x3x3
为什么卷积核一般为奇数不为偶数?
答:
为了保证卷积核的中心点对齐输入图像的像素点,避免卷积结果的失真。如果卷积核的大小是偶数,那么卷积核的中心点就无法精确地落在像素点上,可能会导致边缘信息的模糊。
为了方便进行same padding()的处理,使得输出图像的尺寸和输入图像的尺寸相同。如果卷积核的大小是奇数,那么可以在输入图像的两边对称地补零,使得卷积核的中心点可以滑动到输入图像的边缘。如果卷积核的大小是偶数,那么就需要在输入图像的一边多补一个零,这样就会破坏图像的对称性。
为了更好地获取中心信息,增加特征的不变性。由于奇数卷积核拥有天然的绝对中心点,因此在做卷积的时候能更好地获取到中心这样的概念信息。这样可以增加特征的平移、旋转、尺度等不变性,使网络更鲁棒。
2、感受野:若卷积核为3,则感受野大小为3x3
3、卷积层:若是3通道的图,核为3,则有3个3x3的权重矩阵(或者也叫过滤器)
参数:
步长(stride):2,则每次移动2个像素
填充(padding):1,则周围1圈填充为0(默认填充0),目的:为了提取边缘特征。
3、池化层:(或者也叫下采样层)作用:
降低信息冗余:池化层可以通过对输入数据进行局部聚合,去除一些不必要的细节,只保留最显著的特征,从而减少信息的重复和噪声。
增加特征不变性:池化层可以使特征对输入数据的一些微小变化(如平移、旋转、缩放等)不敏感,提高特征的鲁棒性和泛化能力。
防止过拟合:池化层可以通过减少参数量,降低模型的复杂度,避免模型在训练数据上过度拟合,提高模型的泛化能力。
于是一个中间线段全连接的过程变为:卷积层->激活函数->池化层
以最大池化层举例:(最大池化较平均池化实践上效果较好)参数:核,步长,填充
nn.MaxPool2d(2, 2) #第一个2是池化核大小,第二个2是步长,padding默认为0
F.max_pool2d(x, 2) # 最大池化层 2表示池化核大小,步长默认为2,默认padding为0
4、全连接层之前:(最后一层前的展平)
显而易见,卷积层和池化层的输出是一个张量,而全连接层输入为一个向量,为了使两者能够相互连接,需要将张量展平成向量,以匹配全连接层的输入维度。
全连接层的作用是将卷积层和池化层提取的特征进行组合和映射,得到最终的分类或回归结果。为了实现这个功能,需要将输入数据的所有元素都参与计算,而不是只考虑局部的信息。因此,需要将输入数据展平成一维,使得每个元素都能与全连接层的权重相乘。
全连接层的参数数量取决于输入数据的维度和输出数据的维度。如果输入数据的维度过高,那么全连接层的参数数量就会过多,导致模型的复杂度增加,容易出现过拟合的问题。因此,需要将输入数据展平成一维,减少全连接层的参数数量,降低模型的复杂度。
故在全连接层前有个展平(flatten)操作。
# 将输入张量展平为一维向量
x = x.view(-1, 16*5*5)
至此,以第一个提出的卷积神经网络(LeNet)举例:

这里的尺寸大小计算公式为:[(输入宽度 +2x填充 - 内核宽度 ) / 步长 ] + 1
如10x10x16 里的10 =(14+2x0-5)/1 +1
代码:
# 导入 pytorch 库
import torch
import torch.nn as nn
import torch.nn.functional as F
# 定义网络结构
class LeNet(nn.Module):
def __init__(self):
super(LeNet, self).__init__()
# 定义卷积层 1,输入通道数为 1,输出通道数为 6,卷积核大小为 5
self.conv1 = nn.Conv2d(1, 6, 5, padding=2) #默认stride=1,默认padding=0
# 定义卷积层 2,输入通道数为 6,输出通道数为 16,卷积核大小为 5
self.conv2 = nn.Conv2d(6, 16, 5)
# 定义全连接层 1,输入维度为 16x5x5,输出维度为 120
self.fc1 = nn.Linear(16*5*5, 120)
# 定义全连接层 2,输入维度为 120,输出维度为 84
self.fc2 = nn.Linear(120, 84)
# 定义全连接层 3,输入维度为 84,输出维度为 10
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
# 前向传播,先经过卷积层 1 和激活函数
x = F.sigmoid(self.conv1(x))
# 再经过池化层 1
x = F.avg_pool2d(x, 2) #默认stride=2,默认padding=0
# 再经过卷积层 2 和激活函数
x = F.relu(self.conv2(x))
# 再经过池化层 2
x = F.avg_pool2d(x, 2)
# 将输入张量展平为一维向量
x = x.view(-1, 16*5*5)
# 再经过全连接层 1 和激活函数
x = F.sigmoid(self.fc1(x))
# 再经过全连接层 2 和激活函数
x = F.sigmoid(self.fc2(x))
# 再经过全连接层 3
x = self.fc3(x)
# 返回输出
return x
m =LeNet()
print(m)
torch.manual_seed(0)#设置随机种子
x = torch.randn(1, 1, 28, 28) # (1, 1, 32, 32) #1个样本,1个通道,28x28
output = m(x)
print(output)
'''
LeNet(
(conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
(conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
(fc1): Linear(in_features=400, out_features=120, bias=True)
(fc2): Linear(in_features=120, out_features=84, bias=True)
(fc3): Linear(in_features=84, out_features=10, bias=True)
)
tensor([[-0.0218, -0.0131, -0.5542, 0.2534, 0.2028, -0.2585, -0.1112, 0.0399,
-0.2317, -0.0391]], grad_fn=<AddmmBackward0>)
'''
论文中的阐述

根据论文描述
(5,32)/1,2 x2 表示卷积核为5,输出通道为32(或者说32个滤波器),,步长为1,填充为2。
x2表示级联卷积核,即在第一个卷积层上再应用一个卷积层,好处:1、增强模型表达能力。2、减少网络计算参数。
例: ConvolutionalLayer(1, 32, 5, 1, 2),
ConvolutionalLayer(32, 32, 5, 1, 2),
2/2,0 表示,池化层的核为2,步长为2,填充为0。
选择max-pooling作为池化方法,PReLU为激活函数(官网PReLU)。
计算公式:如果输入特征图的高度和宽度为 H 和 W,卷积核的大小为 K,步长为 S,填充为 P,那么输出特征图的高度和宽度为: (这里是整除:只取商的整数部分,不考虑余数或小数部分)
Hout =(H+2P−K)/S +1
Wout = (W+2P−K)/S +1
这里作者用的模型依然是MINST,形状为28x28x1
经过第一个卷积->(28+2x2-5)/1+1=28 ,通道数为32,则形状为28x28x32。
经过级联卷积->(28+2x2-5)/1+1=28 ,通道数为32,形状为28x28x32。
经过池化->(28+2x0-2)/2+1 =14,通道数不变,形状为14x14x32。
经过第二个卷积-> … ),通道数为64,形状为14x14x64。
经过级联卷积->…,形状为14x14x64。
经过池化->…,形状为7x7x64。
经过第三个卷积-> … ),通道数为128,形状为7x7x128。
经过级联卷积->…,形状为7x7x128。
经过池化->(7+2x0-2)/2+1=3 (注意:这里除法是整除),形状为3x3x128。
代码解释
import torch
import torch.nn as nn
from torch.nn import functional as F
import math
class ConvNet(nn.Module):
"""LeNet++ as described in the Center Loss paper.""" # 在中心损失论文中描述的LeNet++
def __init__(self, num_classes):
super(ConvNet, self).__init__() # 继承父类的所有属性 # (28+2*2-5)/1+1=28
self.conv1_1 = nn.Conv2d(1, 32, 5, stride=1, padding=2) # 1表示输入通道数 32表示输出通道数 5表示卷积核大小 stride表示步长 padding表示填充
self.prelu1_1 = nn.PReLU() # PReLU激活函数 PReLU(x)=max(0,x)+a∗min(0,x) # a是一个可学习的参数
self.conv1_2 = nn.Conv2d(32, 32, 5, stride=1, padding=2) # 这一步是为了增加网络的深度
self.prelu1_2 = nn.PReLU() # PReLU激活函数 默认num_parameters=1, init=0.25,device=None, dtype=None
self.conv2_1 = nn.Conv2d(32, 64, 5, stride=1, padding=2)
self.prelu2_1 = nn.PReLU()
self.conv2_2 = nn.Conv2d(64, 64, 5, stride=1, padding=2)
self.prelu2_2 = nn.PReLU()
self.conv3_1 = nn.Conv2d(64, 128, 5, stride=1, padding=2)
self.prelu3_1 = nn.PReLU()
self.conv3_2 = nn.Conv2d(128, 128, 5, stride=1, padding=2)
self.prelu3_2 = nn.PReLU()
self.fc1 = nn.Linear(128*3*3, 2) # 全连接层 128*3*3表示输入维度 2表示输出维度 3=28/2/2/2
self.prelu_fc1 = nn.PReLU() # PReLU激活函数
self.fc2 = nn.Linear(2, num_classes) # 全连接层
def forward(self, x):
x = self.prelu1_1(self.conv1_1(x)) #
x = self.prelu1_2(self.conv1_2(x))
x = F.max_pool2d(x, 2) # 最大池化层 2表示池化核大小,步长默认为2,默认padding为0
x = self.prelu2_1(self.conv2_1(x))
x = self.prelu2_2(self.conv2_2(x))
x = F.max_pool2d(x, 2)
x = self.prelu3_1(self.conv3_1(x))
x = self.prelu3_2(self.conv3_2(x))
x = F.max_pool2d(x, 2)
#.view()表示改变维度 -1表示自动计算
x = x.view(-1, 128*3*3) # 将x展平 128*3*3表示展平后的维度
x = self.prelu_fc1(self.fc1(x)) # 这里 输出2维
y = self.fc2(x) # 这里 输出num_classes维
return x, y
# Factory function to create model # 工厂函数创建模型
__factory = {
'cnn': ConvNet, # 卷积神经网络
}
def create(name, num_classes):
if name not in __factory.keys():
raise KeyError("Unknown model: {}".format(name))
return __factory[name](num_classes) # name表示模型名称 num_classes表示类别数
if __name__ == '__main__':
pass
运用
import models
model =models.create('cnn',10) #调用models.py中的create函数
print(model)
print(model.parameters()) #打印模型的参数
#model.train() #设置模型为训练模式
model.eval() #设置模型为评估模式 #model.train(False) #设置模型为评估模式
print(model.training) #打印模型的模式
补充:(datasets.py)
transform基础
参考:Pytorch基本操作(4)——torchvision中的transforms的使用
代码解释
import torch
import torchvision
from torch.utils.data import DataLoader
import transforms
class MNIST(object):
def __init__(self, batch_size, use_gpu, num_workers):
# 数据预处理
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,)) # 均值和标准差 0.1307是均值 0.3081是标准差
])# ToTensor()将PIL Image或者numpy.ndarray转化为tensor,并且归一化到[0, 1.0]之间
# Normalize(mean, std, inplace=False) mean是均值 std是标准差 inplace表示是否原地操作
# transforms.Compose 将多个transform组合起来使用
# 数据加载
pin_memory = True if use_gpu else False # 如果使用GPU则pin_memory=True pin_memory表示是否将数据保存在锁页内存中,这样可以加速GPU数据的转移
# torchvision.datasets.MNIST()表示加载MNIST数据集 root表示数据集存放的目录 train表示是否加载训练集 download表示是否下载 transform表示数据预处理
trainset = torchvision.datasets.MNIST(root='./data/mnist', train=True, download=True, transform=transform)# 训练集
# torch.utils.data.DataLoader()表示将数据集加载到DataLoader中 batch_size表示每个batch的大小 shuffle表示是否打乱数据集 num_workers表示加载数据的线程数 pin_memory表示是否将数据保存在pin memory中
trainloader = torch.utils.data.DataLoader(
trainset, batch_size=batch_size, shuffle=True,
num_workers=num_workers, pin_memory=pin_memory,
)
testset = torchvision.datasets.MNIST(root='./data/mnist', train=False, download=True, transform=transform)# 测试集
testloader = torch.utils.data.DataLoader(
testset, batch_size=batch_size, shuffle=False,
num_workers=num_workers, pin_memory=pin_memory,
)
self.trainloader = trainloader
self.testloader = testloader
self.num_classes = 10 # 类别数
__factory = {
'mnist': MNIST,
}
def create(name, batch_size, use_gpu, num_workers):
if name not in __factory.keys():
raise KeyError("Unknown dataset: {}".format(name))
return __factory[name](batch_size, use_gpu, num_workers)
代码运用
import datasets
data =datasets.create('mnist',batch_size=10, use_gpu=False, num_workers=4) #调用datasets.py中的create函数
print(data)
结果:
首次是如下:

打印训练集
import datasets
data =datasets.create('mnist',batch_size=10, use_gpu=False, num_workers=4) #调用datasets.py中的create函数
print(data)
trainloader = data.trainloader
testloader = data.testloader
for i, (inputs, labels) in enumerate(trainloader):#遍历训练集
print(inputs.shape)
print(labels)
break
结果:
<datasets.MNIST object at 0x000002779E097190>
torch.Size([10, 1, 28, 28])
tensor([6, 9, 8, 3, 0, 3, 8, 2, 7, 3])
设置batch_size为10,所以这个为10。
输入为10张1通道的28x28的图。
标签为手写数字的真实值。
transforms.py
注意这里的import transform
相当于下面两句:
from torchvision import transforms
from PIL import Image
原因:transforms.py里的class没用到
from torchvision.transforms import *
from PIL import Image
class ToGray(object):
"""
Convert image from RGB to gray level.
"""
def __call__(self, img):
return img.convert('L') # 转换为灰度图像
补充:(utils.py)
代码解释
import os
import sys
import errno # 异常模块
import shutil # 文件操作
import os.path as osp # os.path 模块主要用于文件的属性获取、文件、目录的创建、删除和文件的路径名的操作
import torch
# 创建文件夹
def mkdir_if_missing(directory):
if not osp.exists(directory): # 如果文件夹不存在
try:
os.makedirs(directory)
except OSError as e:
if e.errno != errno.EEXIST: # 如果错误码不是文件已存在
raise
class AverageMeter(object):
"""Computes and stores the average and current value.# 计算并存储平均值和当前值
Code imported from https://github.com/pytorch/examples/blob/master/imagenet/main.py#L247-L262
"""
def __init__(self):
self.reset()
def reset(self):
self.val = 0 # 当前值
self.avg = 0 # 平均值
self.sum = 0 # 总和
self.count = 0 # 计数
def update(self, val, n=1): # 更新
self.val = val # 当前值
self.sum += val * n # 总和
self.count += n # 计数
self.avg = self.sum / self.count # 平均值
def save_checkpoint(state, is_best, fpath='checkpoint.pth.tar'): #state表示模型的状态 is_best表示是否是最好的模型 fpath表示模型保存的路径
mkdir_if_missing(osp.dirname(fpath)) # 创建文件夹
torch.save(state, fpath) # 保存模型
if is_best: # 如果是最好的模型
#它的意思是将 fpath 这个文件复制到 fpath 所在目录下的 best_model.pth.tar 这个文件中。
shutil.copy(fpath, osp.join(osp.dirname(fpath), 'best_model.pth.tar')) # 复制模型 fpath表示源文件 best_model.pth.tar表示目标文件 osp.join()表示将多个路径组合后返回
class Logger(object):
"""
Write console output to external text file. # 将控制台输出写入外部文本文件
Code imported from https://github.com/Cysu/open-reid/blob/master/reid/utils/logging.py.
"""
def __init__(self, fpath=None): #__init__是一种特殊的方法,被称为类的构造函数或初始化方法,当创建了这个类的实例时就会调用这个方法
self.console = sys.stdout # 控制台输出
self.file = None
if fpath is not None:
mkdir_if_missing(os.path.dirname(fpath))
self.file = open(fpath, 'w') # 打开文件
def __del__(self): #__del__是一种特殊的方法,被称为析构方法,当一个对象被销毁时,析构方法会被调用
self.close()
def __enter__(self): #__enter__和__exit__是一对方法,用于定义一个上下文管理器 #调用with语句时,会执行__enter__方法
pass
def __exit__(self, *args): # 退出
self.close()
def write(self, msg): # 写入
self.console.write(msg) # 控制台输出
if self.file is not None:
self.file.write(msg)
def flush(self): # 刷新
self.console.flush()
if self.file is not None:
self.file.flush()
os.fsync(self.file.fileno()) # 将文件描述符对应的文件写入磁盘
def close(self):
self.console.close() # 关闭控制台
if self.file is not None:
self.file.close() # 关闭文件
代码应用
import os.path as osp
import sys
from utils import AverageMeter, Logger
#osp.join('test', 'log_' + "test" + '.txt') #拼接字符串 #保存在test/log_test.txt
sys.stdout = Logger(osp.join('test', 'log_' + "test" + '.txt')) # 保存训练日志 #将标准输出重定向到文件
losses = AverageMeter() #创建一个AverageMeter对象
losses.update(1, 10) #更新losses的值 #现在losses的值为1,个数为10
print(losses.avg) #打印losses的平均值
print(losses.val) #打印losses的值
print(losses.sum) #打印losses的和
print(losses.count) #打印losses的个数
sys.stdout.write('This is a log message\n')
输出:

并且在当前文件生成一个文件夹,在此文件夹下生成日志文件。

main.py解释
argparse模块应用
参考:
1、argparse — 命令行选项、参数和子命令解析器
2、argparse库教程(超易懂)
简单运用:
sum.py
# 导入 argparse 模块
import argparse
# 创建一个 ArgumentParser 对象
parser = argparse.ArgumentParser(description='计算两个数的和')
# 添加两个位置参数
parser.add_argument('a', type=int, help='第一个加数')
parser.add_argument('b', type=int, help='第二个加数')
# 解析命令行
args = parser.parse_args()
# 打印结果
print(args.a + args.b)
注:默认type是str,所以这里要相加的话,得用整数
结果:

代码解释
# argparse.ArgumentParser() 创建一个ArgumentParser对象 用来处理命令行参数
parser = argparse.ArgumentParser("Center Loss Example")
# dataset # 数据集
# add_argument() 方法用于指定程序需要接受的命令参数
parser.add_argument('-d', '--dataset', type=str, default='mnist', choices=['mnist']) # 选择数据集 例:python main.py -d mnist
parser.add_argument('-j', '--workers', default=4, type=int,
help="number of data loading workers (default: 4)") # 数据加载工作线程数 例:python main.py -j 4 #-j表示短名称
# optimization # 优化
parser.add_argument('--batch-size', type=int, default=128) # 批大小
parser.add_argument('--lr-model', type=float, default=0.001, help="learning rate for model") # 学习率
parser.add_argument('--lr-cent', type=float, default=0.5, help="learning rate for center loss") # 中心损失学习率
parser.add_argument('--weight-cent', type=float, default=1, help="weight for center loss") # 中心损失权重
parser.add_argument('--max-epoch', type=int, default=100) # 最大迭代次数
parser.add_argument('--stepsize', type=int, default=20) # 学习率下降间隔 : 每隔多少个epoch下降一次
parser.add_argument('--gamma', type=float, default=0.5, help="learning rate decay") # 学习率衰减 : 学习率下降的倍数 比如0.5表示学习率减半
# model # 模型
parser.add_argument('--model', type=str, default='cnn') # 模型选择
# misc # 其他
parser.add_argument('--eval-freq', type=int, default=10) # 评估频率
parser.add_argument('--print-freq', type=int, default=50) # 打印频率
parser.add_argument('--gpu', type=str, default='0') # GPU
parser.add_argument('--seed', type=int, default=1) # 随机种子
parser.add_argument('--use-cpu', action='store_true') # 是否使用CPU action='store_true' 表示如果有这个参数则为True
parser.add_argument('--save-dir', type=str, default='log') # 保存路径 保存训练日志 保存在log文件夹下
parser.add_argument('--plot', action='store_true', help="whether to plot features for every epoch") # 是否绘制特征图
args = parser.parse_args() # 解析参数 保存到args中
plot_features()函数
matplotlib模块应用
import matplotlib.pyplot as plt
# 生成一些随机数据
x = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
y = [2, 4, 6, 8, 10, 12, 14, 16, 18, 20]
colors = ['C0', 'C1', 'C2', 'C3', 'C4', 'C5', 'C6', 'C7', 'C8', 'C9'] # 颜色
for i in range(10):
plt.scatter(x[i], y[i], c=colors[i]) # 画散点 #或c='C'+str(i)
plt.legend(['0', '1', '2', '3', '4', '5', '6', '7', '8', '9'], loc='upper right')#图例 upper right表示右上角
plt.show()

若保存:
import matplotlib.pyplot as plt
# 生成一些随机数据
x = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
y = [2, 4, 6, 8, 10, 12, 14, 16, 18, 20]
colors = ['C0', 'C1', 'C2', 'C3', 'C4', 'C5', 'C6', 'C7', 'C8', 'C9'] # 颜色
for i in range(10):
plt.scatter(x[i], y[i], c=colors[i]) # 画散点 #或c='C'+str(i)
plt.legend(['0', '1', '2', '3', '4', '5', '6', '7', '8', '9'], loc='upper right')#图例 upper right表示右上角
plt.savefig('test.png', bbox_inches='tight') # bbox_inches='tight'表示将图片四周的空白部分裁剪掉
plt.close() # 关闭绘图
代码解释
import matplotlib.pyplot as plt
import os
import os.path as osp
import torch
def plot_features(features, labels, num_classes, epoch, prefix):
"""Plot features on 2D plane.# 在2D平面上绘制特征
Args:
features: (num_instances, num_features). # 特征
labels: (num_instances). # 标签
"""
colors = ['C0', 'C1', 'C2', 'C3', 'C4', 'C5', 'C6', 'C7', 'C8', 'C9'] # 颜色
# 画散点
for label_idx in range(num_classes):
plt.scatter( #如: label_idx=0时,取对应labels==0的features的横坐标和纵坐标
features[labels==label_idx, 0], # x坐标 labels==label_idx表示labels中等于label_idx的索引 0 取第0列的元素
features[labels==label_idx, 1], # y坐标 1 取第1列的元素
c=colors[label_idx], # 颜色
s=1, # 点的大小
)
# plt.legend() 图例
plt.legend(['0', '1', '2', '3', '4', '5', '6', '7', '8', '9'], loc='upper right') #'upper right'表示右上角
# 保存
dirname = osp.join(save_dir, prefix) #prefix意为前缀 保存在save_dir/prefix文件夹下
if not osp.exists(dirname):
os.mkdir(dirname)
save_name = osp.join(dirname, 'epoch_' + str(epoch+1) + '.png')
plt.savefig(save_name, bbox_inches='tight') # bbox_inches='tight'表示将图片四周的空白部分裁剪掉
plt.close() # 关闭绘图
代码运用
# 生成一些随机的特征和标签
torch.manual_seed(0) #设置随机种子
features = torch.randn(100, 2) # 100个样本,每个样本有2个特征 #因为输出的是二维的,所以这里是2
#print(features)
labels = torch.randint(0, 10, (100,)) # 100个样本,每个样本属于0-9中的一个类别
#print(labels)
num_classes = 10 # 类别个数
epoch = 0 # 训练轮数
prefix = 'test' # 文件夹前缀
save_dir = 'test' # 保存的文件夹
# 调用 plot_features 函数
plot_features(features, labels, num_classes, epoch, prefix)
结果:

train()
1、当未收敛时:
2、迭代次数t+1
3、计算损失函数 L=Ls+Lc
4、计算反向传播误差(即梯度)
5、更新w
6、更新cj
7、更新θc
8、结束
nn.CrossEntropyLoss()
计算交叉熵损失函数
公式:

代码:
import torch
import torch.nn as nn
# 创建一个交叉熵损失函数的对象
criterion = nn.CrossEntropyLoss()
#设置随机种子
torch.manual_seed(0)
# 生成一些随机的输出和标签 rand返回一个张量,包含了从区间[0, 1)的均匀分布中抽取的一组随机数
#生成随机数为0-1的10x5的张量 randn返回一个张量,包含了从标准正态分布(均值为0,方差为 1)中抽取的一组随机数
output = torch.rand(10, 5) # 10个样本,每个样本有5个类别的概率
label = torch.randint(0, 5, (10,)) # 10个样本,每个样本属于0-4中的一个类别
print(output)
print(label)
# 计算损失
loss = criterion(output, label)
# 打印损失
print(loss)
这里的损失计算的是输出值和真实值之间的损失。
结果:
output:每一行是一个样本的预测概率,每一列是一个类别的预测概率。output 的每个元素是一个实数,表示对应样本和类别的预测概率,取值范围是 (0, 1)。
例如,如果 output 的第一个元素是 0.8,表示第一个样本预测属于第一个类别的概率是 0.4963。
label:一个一维的张量,表示样本的类别标签,与 output的行数相同。label 的每个元素是一个整数,表示对应样本的真实类别,取值范围是 [0, M-1],其中 M 是类别数量。
例如,如果 label 的第一个元素是 0,表示第一个样本的真实类别是 0。
tensor([[0.4963, 0.7682, 0.0885, 0.1320, 0.3074],
[0.6341, 0.4901, 0.8964, 0.4556, 0.6323],
[0.3489, 0.4017, 0.0223, 0.1689, 0.2939],
[0.5185, 0.6977, 0.8000, 0.1610, 0.2823],
[0.6816, 0.9152, 0.3971, 0.8742, 0.4194],
[0.5529, 0.9527, 0.0362, 0.1852, 0.3734],
[0.3051, 0.9320, 0.1759, 0.2698, 0.1507],
[0.0317, 0.2081, 0.9298, 0.7231, 0.7423],
[0.5263, 0.2437, 0.5846, 0.0332, 0.1387],
[0.2422, 0.8155, 0.7932, 0.2783, 0.4820]])
tensor([0, 4, 3, 1, 1, 0, 3, 1, 1, 2])
tensor(1.5950)
一般更新步骤
参考:
1、PyTorch中为什么要进行梯度清零
2、PyTorch中在反向传播前为什么要手动将梯度清零?
3、pytorch是如何实现对loss进行反向传播计算梯度的?
# let us write a training loop
torch.manual_seed(42) #设置随机种子
epochs = 200 #迭代次数
for epoch in range(epochs):
model_1.train() #训练模式
pred = model_1(data) # 模型训练
loss = loss_fn(pred,label) #计算损失
optimizer.zero_grad() #梯度清零
loss.backward() #反向传播
optimizer.step() #梯度更新
若有trainloader:
# let us write a training loop
torch.manual_seed(42) #设置随机种子
epochs = 200 #迭代次数
for epoch in range(epochs):
model_1.train() #训练模式
for i, (data, labels) in enumerate(trainloader):
pred = model_1(data) # 模型训练
loss = loss_fn(pred,label) #计算损失
optimizer.zero_grad() #梯度清零
loss.backward() #反向传播
optimizer.step() #梯度更新
只要optimizer.zero_grad() 满足在反向传播之前就行。(也有第一步就进行梯度清零的)
目的:为了避免在每次迭代中梯度累加,确保每个批次的训练都是从零开始计算梯度,从而保证了梯度更新的准确性。
在前馈传播期间,权重被分配给输入,在第一次迭代之后,权重被初始化,模型从样本(输入)中学到了什么。当我们开始反向传播时我们想要更新权值以使代价函数的损失最小。所以我们清除了之前的权值以便得到更好的权值。我们在训练中一直这样做,在测试中我们不会这样做,因为我们在训练时间得到了最适合我们数据的权重。
例子:

回过头来:
1、当未收敛时:for epoch in range(epochs): 进行了1、2
2、迭代次数t+1
3、计算损失函数 L=Ls+Lc
model_1.train() #训练模式
pred = model_1(data) # 模型训练
loss = loss_fn(pred,label) #计算损失 进行了3
4、计算反向传播误差(即梯度)
5、更新w
6、更新cj
7、更新θc
optimizer.zero_grad() #梯度清零
loss.backward() #反向传播
optimizer.step() #梯度更新 进行了5 、6、7
8、结束
简单例子
下面是一个使用 PyTorch 的简单示例,实现了一个线性回归模型,并用随机梯度下降法(SGD)进行梯度更新。
import torch
import torch.nn as nn
import torch.optim as optim
#设置随机种子
torch.manual_seed(0)
# 生成一些随机的输入和标签
x = torch.randn(100, 1) # 100个样本,每个样本有1个特征 randn
y = 3 * x + 5 + torch.randn(100, 1) # 100个样本,每个样本有1个标签,服从 y = 3x + 5 + 噪声 的分布
# 定义一个简单的线性模型
model = nn.Linear(1, 1) # 输入维度是1,输出维度是1
# 定义一个均方误差损失函数
criterion = nn.MSELoss()
# 定义一个随机梯度下降优化器
optimizer = optim.SGD(model.parameters(), lr=0.01) # 学习率是0.01
# 训练100个迭代
for epoch in range(100):
# 清零梯度
optimizer.zero_grad()
# 得到预测结果
output = model(x)
# 计算损失
loss = criterion(output, y)
# 反向传播,计算梯度
loss.backward()
# 更新参数
optimizer.step()
# 打印损失
print(f"Epoch {epoch}, loss {loss.item():.4f}")
# 打印模型参数
print(model.weight)
print(model.bias)
部分结果:

代码解释
def train(model, criterion_xent, criterion_cent,
optimizer_model, optimizer_centloss,
trainloader, use_gpu, num_classes, epoch):
model.train() # 训练模式
xent_losses = AverageMeter() # 交叉熵损失 #掉用utils.py中的AverageMeter类
cent_losses = AverageMeter() # 中心损失
losses = AverageMeter() # 总损失
if args.plot: # 是否绘制特征图
all_features, all_labels = [], []
for batch_idx, (data, labels) in enumerate(trainloader):
if use_gpu:
data, labels = data.cuda(), labels.cuda()
features, outputs = model(data) # 前向传播得出2维特征和num_classes维输出
loss_xent = criterion_xent(outputs, labels) #outputs表示模型的输出 labels表示真实标签 计算输出值和真实值之间的交叉熵损失
loss_cent = criterion_cent(features, labels) #!!! 计算2维的特征和标签之间的中心损失(因为中心损失是在二维里提出的)
loss_cent *= args.weight_cent # 中心损失乘以权重
loss = loss_xent + loss_cent # 总损失
optimizer_model.zero_grad() # 梯度清零 防止梯度累加
optimizer_centloss.zero_grad() # 梯度清零
loss.backward() # 反向传播求梯度
optimizer_model.step() # 更新模型参数
# by doing so, weight_cent would not impact on the learning of centers
for param in criterion_cent.parameters():
param.grad.data *= (1. / args.weight_cent) # 中心损失函数的梯度 #乘以1/args.weight_cent
optimizer_centloss.step() # 更新中心损失参数
losses.update(loss.item(), labels.size(0)) # 更新总损失 loss.item()表示取出loss的值 labels.size(0)表示取出labels的大小 即batch_size
xent_losses.update(loss_xent.item(), labels.size(0))
cent_losses.update(loss_cent.item(), labels.size(0))
if args.plot:
if use_gpu:
all_features.append(features.data.cpu().numpy()) # .data表示取出数据 cpu表示将数据放到CPU上 numpy表示将数据转换为numpy格式
all_labels.append(labels.data.cpu().numpy())
else:
all_features.append(features.data.numpy())
all_labels.append(labels.data.numpy())
# 打印
if (batch_idx+1) % args.print_freq == 0: # 每隔多少个batch打印一次
print("Batch {}/{}\t Loss {:.6f} ({:.6f}) XentLoss {:.6f} ({:.6f}) CenterLoss {:.6f} ({:.6f})" \
.format(batch_idx+1, len(trainloader), losses.val, losses.avg, xent_losses.val, xent_losses.avg, cent_losses.val, cent_losses.avg))
if args.plot: #[np.array([[1, 2, 3], [4, 5, 6]],np.array([[7, 8, 9], [10, 11, 12]])] -> np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]])
all_features = np.concatenate(all_features, 0) #np.concatenate表示将多个numpy数组进行合并 axis=0表示按行合并
all_labels = np.concatenate(all_labels, 0)
plot_features(all_features, all_labels, num_classes, epoch, prefix='train')
小细节有的在main()里补充。
test()
一般测试步骤
# 假设 model 是已经训练好的模型,criterion 是损失函数
# test_loader 是用于测试的 DataLoader
model.eval() # 设置模型为评估模式
test_loss = 0
correct = 0
with torch.no_grad(): # 关闭梯度计算
for data, target in test_loader:
output = model(data)
test_loss += criterion(output, target).item() # 累加损失.item()返回一个标量
pred = output.argmax(dim=1, keepdim=True) # 获取预测结果 argmax返回最大值的索引
correct += pred.eq(target.view_as(pred)).sum().item() #.eq是比较两个tensor是否相等,相等返回1,不相等返回0 .sum()返回相等的个数
test_loss /= len(test_loader.dataset) #计算平均损失
test_accuracy = 100. * correct / len(test_loader.dataset)
print(f'Test set: Average loss: {test_loss:.4f}, Accuracy: {correct}/{len(test_loader.dataset)} ({test_accuracy:.0f}%)')
代码解释
def test(model, testloader, use_gpu, num_classes, epoch):
model.eval() # 测试模式
correct, total = 0, 0 # 正确数 总数
if args.plot:
all_features, all_labels = [], []
with torch.no_grad(): # 不需要计算梯度
for data, labels in testloader:
if use_gpu:
data, labels = data.cuda(), labels.cuda()
features, outputs = model(data)
predictions = outputs.data.max(1)[1] # 取出最大值的索引 .data 表示取出数据 max(1)表示按行取最大值 [1]表示取出索引
total += labels.size(0) # 更新总数
correct += (predictions == labels.data).sum() # 更新正确数
if args.plot:
if use_gpu:
all_features.append(features.data.cpu().numpy())
all_labels.append(labels.data.cpu().numpy())
else:
all_features.append(features.data.numpy())
all_labels.append(labels.data.numpy())
if args.plot:
all_features = np.concatenate(all_features, 0)
all_labels = np.concatenate(all_labels, 0)
plot_features(all_features, all_labels, num_classes, epoch, prefix='test')
acc = correct * 100. / total # 准确率 %前的数
err = 100. - acc # 错误率
return acc, err
其中关于outputs.data.max(1)[1]的解释
import torch
# 设置随机种子
torch.manual_seed(0)
# 生成一些随机的输出和标签
output = torch.rand(2, 5) # 2个样本,每个样本有5个类别的概率
print(output)
print(output.data.max(1, keepdim=True)) #返回每一行的最大值和最大值的索引 keepdim=True 保持原来的维度
print(output.data.max(1)[1]) #返回每一行最大值的索引
'''
tensor([[0.4963, 0.7682, 0.0885, 0.1320, 0.3074],
[0.6341, 0.4901, 0.8964, 0.4556, 0.6323]])
torch.return_types.max(
values=tensor([[0.7682],
[0.8964]]),
indices=tensor([[1],
[2]]))
tensor([1, 2])
'''
main()
参数
这里解释下下面代码中,model.parameters()和criterion.parameters()里的参数是什么。
optimizer_model = torch.optim.SGD(model.parameters(), lr=args.lr_model, weight_decay=5e-04, momentum=0.9)
optimizer_centloss = torch.optim.SGD(criterion_cent.parameters(), lr=args.lr_cent)
先看model.parameters(),用一个简单的模型举例。
import torch.nn as nn
import torch.optim as optim
# 设置随机种子
torch.manual_seed(0)
# 定义一个简单的神经网络模型
class SimpleModel(nn.Module):
def __init__(self):
super(SimpleModel, self).__init__()
self.fc1 = nn.Linear(10, 5) #10个输入,5个输出
self.fc2 = nn.Linear(5, 2)
def forward(self, x):
x = self.fc1(x)
x = self.fc2(x)
return x
# 实例化模型
model = SimpleModel()
# 使用 model.parameters() 获取所有参数
for param in model.parameters():
print(param)
# 使用 model.named_parameters() 获取所有参数,以及参数名
for name, param in model.named_parameters():
print(name, param.size())
print(model.fc1.weight)
#x = torch.randn(2, 10) # 2个样本,每个样本有10个特征
结果:
Parameter containing:
tensor([[-0.0024, 0.1696, -0.2603, -0.2327, -0.1218, 0.0848, -0.0063, 0.2507,
-0.0281, 0.0837],
[-0.0956, -0.0622, -0.3021, -0.2094, -0.1304, 0.0117, 0.1250, 0.1897,
-0.2144, -0.1377],
[ 0.1149, 0.2626, -0.0651, 0.2366, -0.0510, 0.0335, 0.2863, -0.2934,
-0.1991, -0.0801],
[-0.1233, 0.2732, -0.2050, -0.1456, -0.2209, -0.2962, -0.1846, 0.2718,
0.1411, 0.1533],
[ 0.0166, -0.1621, 0.0535, -0.2953, -0.2285, -0.1630, 0.1995, 0.1854,
-0.1402, -0.0114]], requires_grad=True)
Parameter containing:
tensor([0.2022, 0.3144, 0.1255, 0.0427, 0.2120], requires_grad=True)
Parameter containing:
tensor([[-0.2633, 0.0833, -0.3467, -0.3100, -0.2310],
[ 0.2024, 0.1799, -0.2649, 0.1351, 0.2455]], requires_grad=True)
Parameter containing:
tensor([-0.0564, 0.0171], requires_grad=True)
fc1.weight torch.Size([5, 10])
fc1.bias torch.Size([5])
fc2.weight torch.Size([2, 5])
fc2.bias torch.Size([2])
Parameter containing:
tensor([[-0.0024, 0.1696, -0.2603, -0.2327, -0.1218, 0.0848, -0.0063, 0.2507,
-0.0281, 0.0837],
[-0.0956, -0.0622, -0.3021, -0.2094, -0.1304, 0.0117, 0.1250, 0.1897,
-0.2144, -0.1377],
[ 0.1149, 0.2626, -0.0651, 0.2366, -0.0510, 0.0335, 0.2863, -0.2934,
-0.1991, -0.0801],
[-0.1233, 0.2732, -0.2050, -0.1456, -0.2209, -0.2962, -0.1846, 0.2718,
0.1411, 0.1533],
[ 0.0166, -0.1621, 0.0535, -0.2953, -0.2285, -0.1630, 0.1995, 0.1854,
-0.1402, -0.0114]], requires_grad=True)
我们可以看到,这里的权重矩阵W是5x10的形式,而输入假设为X:2x10的数据,故要进行矩阵乘法前,须对矩阵进行转置,则变为WT:10x5矩阵,偏置b为1x5的形式,所以第一个nn.Linear(10, 5)结果为y =X@WT +b(@表示举证乘法)。
至于这里的初始化的权重是怎么随机化的,我在nn.Linear(按ctrl进源代码)的源代码中找到出处: 用了这个init.kaiming_uniform_方法。
可以见:这里 的解释
def reset_parameters(self) -> None:
# Setting a=sqrt(5) in kaiming_uniform is the same as initializing with
# uniform(-1/sqrt(in_features), 1/sqrt(in_features)). For details, see
# https://github.com/pytorch/pytorch/issues/57109
init.kaiming_uniform_(self.weight, a=math.sqrt(5))
if self.bias is not None:
fan_in, _ = init._calculate_fan_in_and_fan_out(self.weight)
bound = 1 / math.sqrt(fan_in) if fan_in > 0 else 0
init.uniform_(self.bias, -bound, bound)
类似的criterion.parameters()的参数里也是差不多
只是这里的参数是我们自己定义的
self.centers = nn.Parameter(torch.randn(self.num_classes, self.feat_dim))
与上面的权重矩阵类似,输入的维度在后面,输出的维度在前面,[输出的维度,输入的维度]。
这也解释了为什么后面有转置的操作,为了矩阵相乘或相加。
于是,我们知道了神经网络要“学习”的参数就是这些参数了,当这些参数达到一个比较好的符合损失函数的标准时,这些参数就可以帮助我们进行分类等任务。而更新这些的方法,类似于梯度下降法。
将光标放到parameters()上: 显示

这通常传递给优化器。
torch.optim.SGD
参考:
1、SGD pytorch官方文档
2、PyTorch优化算法:torch.optim.SGD的参数详解和应用
torch.optim.SGD(params, lr=, momentum=0, dampening=0, weight_decay=0, nesterov=False)
1、params(必须参数): 这是一个包含了需要优化的参数(张量)的迭代器,例如模型的参数 model.parameters()。
1、lr(必须参数): 学习率(learning rate)。它是一个正数,控制每次参数更新的步长。较小的学习率会导致收敛较慢,较大的学习率可能导致震荡或无法收敛。
3、momentum(默认值为 0): 动量(momentum)是一个用于加速 SGD 收敛的参数。它引入了上一步梯度的指数加权平均。通常设置在 0 到 1 之间。当 momentum 大于 0 时,算法在更新时会考虑之前的梯度,有助于加速收敛。
4、dampening(默认值为 0): 阻尼项,用于减缓动量的速度。在某些情况下,为了防止动量项引起的震荡,可以设置一个小的 dampening 值。
5、weight_decay(默认值为 0): 权重衰减,也称为 L2 正则化项。它用于控制参数的幅度,以防止过拟合。通常设置为一个小的正数。
6、nesterov(默认值为 False): Nesterov 动量。当设置为 True 时,采用 Nesterov 动量更新规则。Nesterov 动量在梯度更新之前先进行一次预测,然后在计算梯度更新时使用这个预测。
由官方的SVD中给的例子得出:
通常的梯度下降为以下几个步骤。
optimizer = torch.optim.SGD(model.parameters(), lr=0.1, momentum=0.9)
optimizer.zero_grad()
loss_fn(model(input), target).backward()
optimizer.step()
注意这里loss.backward()(官方文档)用的链式法则求导(梯度),所以这里loss.backward()只要进行一次,就把两个梯度都算了,其他的步骤要两个。

动量解释:为下方的u,写在t时刻的速度前,为速度的调整量。默认为0。
lr学习率:写在t+1时刻的速度前。 如下:

关于权重衰减项:
参考:How to Use Weight Decay to Reduce Overfitting of Neural Network in Keras
5e-4的由来:发现用此衰减值在CNN模型中获得的效果比较好。

STEPLR
解释代码:
if args.stepsize > 0: # 学习率下降
scheduler = lr_scheduler.StepLR(optimizer_model, step_size=args.stepsize, gamma=args.gamma) # 学习率下降
if args.stepsize > 0: scheduler.step() # 学习率更新
参考:官方STEPLR
在 PyTorch 中,lr_scheduler.StepLR 是一个学习率调度器,它会在每个 step_size 指定的周期后,将优化器中每个参数组的学习率乘以 gamma 参数。这样做可以在训练过程中逐步降低学习率,有助于模型在训练后期稳定并提高性能。
scheduler = lr_scheduler.StepLR(optimizer_model, step_size=args.stepsize, gamma=args.gamma)
step_size 是学习率下降的周期,以 epoch 计。
gamma 是学习率衰减的因子,通常是一个小于 1 的数。
例:
# Assuming optimizer uses lr = 0.05 for all groups
# lr = 0.05 if epoch < 30
# lr = 0.005 if 30 <= epoch < 60
# lr = 0.0005 if 60 <= epoch < 90
# ...
scheduler = StepLR(optimizer, step_size=30, gamma=0.1)
for epoch in range(100):
train(...)
validate(...)
scheduler.step()
使用这个调度器时,你需要在每个 epoch 的训练循环结束后调用 scheduler.step() 来更新学习率。
那为什么给 optimizer_model 做了学习率的下降,没有给 optimizer_centloss做学习率下降?
可能合理的解释:
1、模型参数可能需要更动态的学习率调整来更好地适应数据特征,而中心损失参数可能不需要那么频繁的调整。
2、对中心损失参数使用固定的学习率能够得到更好的结果。
3、中心损失通常用于学习特征的紧凑表示,可能不需要随时间变化的学习率来优化。
4、简化训练过程。
当然,实际上,我们也可以对optimizer_centloss做学习率下降。
main()代码解释
def main():
torch.manual_seed(args.seed) # 设置随机种子
os.environ['CUDA_VISIBLE_DEVICES'] = args.gpu # 设置GPU
use_gpu = torch.cuda.is_available() # 是否使用GPU
if args.use_cpu: use_gpu = False # 如果使用CPU 则不使用GPU
sys.stdout = Logger(osp.join(args.save_dir, 'log_' + args.dataset + '.txt')) # 保存训练日志
if use_gpu:
print("Currently using GPU: {}".format(args.gpu))
cudnn.benchmark = True # 优化卷积运算 #网络的输入数据维度或类型上变化不大的情况下,设置为True可以增加运行效率
torch.cuda.manual_seed_all(args.seed) #为所有的GPU设置随机种子
else:
print("Currently using CPU")
print("Creating dataset: {}".format(args.dataset))
# 创建数据集
dataset = datasets.create(
name=args.dataset, batch_size=args.batch_size, use_gpu=use_gpu,
num_workers=args.workers,
)
# 获取训练集和测试集
trainloader, testloader = dataset.trainloader, dataset.testloader #调用dataset类的trainloader和testloader属性
# 创建模型
print("Creating model: {}".format(args.model))
model = models.create(name=args.model, num_classes=dataset.num_classes) # 调用models.py中的create函数 创造类
if use_gpu:
model = nn.DataParallel(model).cuda() # 使用多GPU nn.DataParallel()表示将模型并行化
criterion_xent = nn.CrossEntropyLoss() # 交叉熵损失
criterion_cent = CenterLoss(num_classes=dataset.num_classes, feat_dim=2, use_gpu=use_gpu) # 中心损失
## 优化器 SGD #model.parameters()表示优化模型参数 lr学习率 weight_decay权重衰减 5e-04 momentum动量0.9
optimizer_model = torch.optim.SGD(model.parameters(), lr=args.lr_model, weight_decay=5e-04, momentum=0.9)
optimizer_centloss = torch.optim.SGD(criterion_cent.parameters(), lr=args.lr_cent)
if args.stepsize > 0: # 学习率下降
scheduler = lr_scheduler.StepLR(optimizer_model, step_size=args.stepsize, gamma=args.gamma) # 学习率下降
start_time = time.time()# 计时
for epoch in range(args.max_epoch):
print("==> Epoch {}/{}".format(epoch+1, args.max_epoch))
train(model, criterion_xent, criterion_cent,
optimizer_model, optimizer_centloss,
trainloader, use_gpu, dataset.num_classes, epoch)
if args.stepsize > 0: scheduler.step() # 学习率更新
# 每隔eval_freq个epoch评估一次
if args.eval_freq > 0 and (epoch+1) % args.eval_freq == 0 or (epoch+1) == args.max_epoch: #
print("==> Test")
acc, err = test(model, testloader, use_gpu, dataset.num_classes, epoch)
print("Accuracy (%): {}\t Error rate (%): {}".format(acc, err))
#
elapsed = round(time.time() - start_time)
elapsed = str(datetime.timedelta(seconds=elapsed)) # 时间格式转换 例:datetime.timedelta(seconds=12345) -> 3:25:45
print("Finished. Total elapsed time (h:m:s): {}".format(elapsed))
总结
至此解释完毕,字数有点多了,有点卡了。
下个博客再讲如何运行。