这篇文章主要是为了构建一种轻客户端的算法。 如果使用SPV 的方式验证交易,每个client上面需要存储非常多的header。使用 proofs of proof-of-work 的方式,使得请客户端仅仅下载少量的区块头就能验证这一条链的安全性,然后再对包含交易的区块进行merkle proof 验证。
这篇工作主要对比的方式就是 NIPoPoW ,之后也会读一下这篇文章。
这篇文章还有一个贡献是,可以应对难度系数可变的情况。特别是在btc中,挖矿的难度稀释时刻在改变,这会导致一个攻击difficulty raising attack 难度提升攻击,但是这个攻击我之前没有听说过。并且网上的资料也不是很全,他主要是出现在一个文章中(L. Bahack, “Theoretical bitcoin attacks with less than half of the computational power (draft),” arXiv preprint arXiv:1312.7013, 2013.),之后读一下。
NIPoPoW 的方法中使用了超级块,虽然他也是只需要对数个区块头,但是区块头非常的大,还是会导致存储比较大的问题。
这篇文章中的方法也是选择使用 O(log n)数量的块头,来验证一条链的合法性。
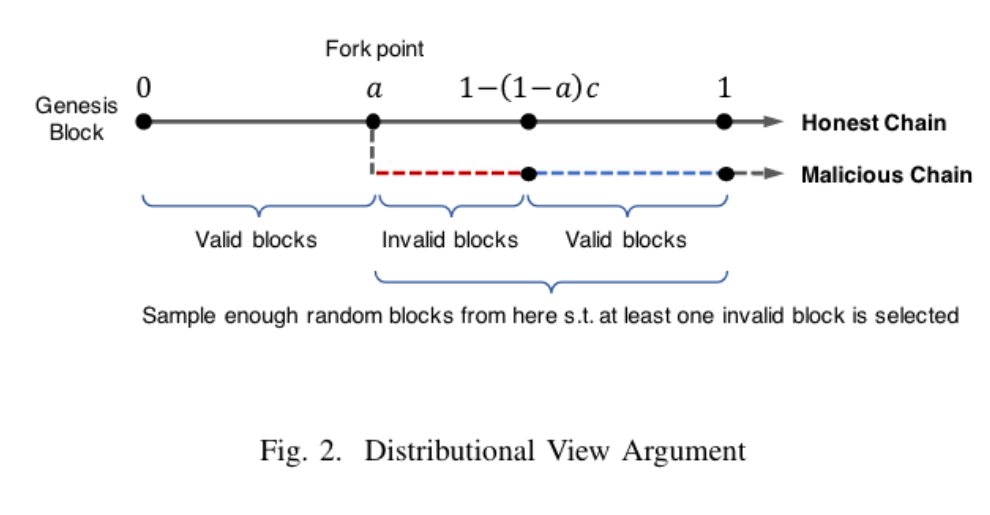
文章中假设恶意节点无法发动51%攻击,恶意节点的数量与诚实节点的数量比值为 c。c < 1
当对手节点(恶意节点)控制诚实链的 c 比例的有效工作量时,可以创建分叉,但是如果分叉链和诚实的链一样长是做不到的,因为恶意节点的算力更少。因此恶意节点会将一些不合法的块塞到链中,用于伪造区块长度。
client 做verifier, 全节点做 prover。
OVERVIEW
verifier 会连接到许多的prover,但是至少有一个prover是诚实的,我们在这里并不考虑日蚀攻击的情况。
第一步,每个prover将自己的 last header 或者 block 发送给verifier,verifier 会首先选择最长的链进行验证。
概率采样协议
我们给出了一个概率密度函数 g(x) 用于表明在高度为x位置的块被采样的概率。
应对难度可变的情况
在难度可变的情况下,工作量并不在用链的长度来证明,而是根据链的累计难度来确定。
我们使用相同的概率密度函数 g(x),只不过此时x不在表明区块的高度,而是表明区块的相对总难度的累计难度。
MMR
比如,我们要查询高度为x的块,但是我们并没有保存整体的块头,恶意节点可能返回任意位置的有效区块来冒充x高度的区块,因此我们需要一个机制来进行保证。
同样的,我们要查询累计难度为 x 的区块,恶意全节点也可以进行造假。
为了确保区块的位置没有篡改,使用Merkle Mountain Range (MMR) 来覆盖所有的区块。保证区块的位置没有发生篡改。
为了准确记录区块的相对难度,也要对MMR 进行改造,以便于对难度进行记录。
Non-Interactive and Transferable FlyClient
在提到非交互性的时候,这篇文章在反复提到 (Fiat-Shamir heuristic) ,这篇文章也看一下。
让证明过程称为非交互的,使用的随机数通过hash 头推导出。
非交互性使 FlyClient 更为实用,因为:
(1) 全节点可以向许多轻客户端发送相同的证明,而无需重新计算;
(2) 客户端可以将证明转发给其他新的轻客户端,后者可以安全地验证证明的正确性。这就减少了证明者和验证者的计算量和带宽开销。
用于确定采样区块的随机性是通过应用于链头的安全散列函数(如 SHA-3)得出的。验证者不仅要检查查询本身,还要检查随机性是否正确。
Attacks Using Variable Difficulty
文章中提到了难度可变的情况下,容易发动难度可变攻击。但实际上,这个难度可变攻击并不是这里的主要解决的问题。在我的理解下,是说系统所认可的并不是链的长度,更是区块的难度。因此在考虑区块抽样的时候,要将衡量的尺度从区块的长度转移的相对难度。
对手模型
对手会从诚实的链上进行分叉,但是对手节点的算力只有诚实节点的c比例。算力不高,恶意节点可以创建和诚实链一样长的分叉,但是只有 c 比例的块是有效的,其他都是编造出来的。
但是对于比较短的分叉,这种分叉也有可能是合法的。
在 PoW 加密货币中,有效链是累计工作量证明最高的链,即最难创建的链。
区块采样策略
对于难度可变 和 不可变 主要的区别就是采样规则的问题,更准确是说采样空间的问题
最重链原则(也称为最大累积工作量原则)是一种在区块链网络中决定最有效、最可信链的方法,特别是在使用工作量证明(Proof of Work, PoW)机制的系统中。与最长链原则不同,最重链原则不仅考虑区块链的长度,也考虑了生成链上每个区块所需的工作量。这意味着,一条链如果拥有最大的累积工作量,即使它的区块数量不是最多的,也被视为主链。
而我们最主要的目标就是最小化采样的规模。
如果我们能够知道,链是从哪里分叉的,那么我们就可以在分叉之后充分的查询,才会有比较高的成功率。但是我们并不知道分叉点在哪里。
我们采用的采样概率密度函数,是一个递增的函数。这样也有道理,概率密度递增,使得更多的查询能够落在每两段的后半段,查询落在分叉之后的链上的概率更大,这样是有更好的效果的。原文中给出了证明,不得不说,原文中的证明非常扎实,但是我没怎么看懂。
因为我们主要在链的末尾进行采样,因此对手主要将生成的合法区块放在末尾。将不合法的区块往前方,这样被采样到假区块的概率才最小。
因此,如果我们进行一次查询,就能查询到虚假区块的概率为
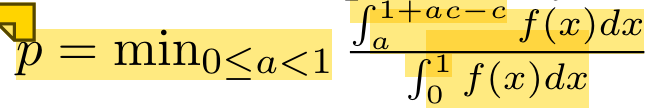
我们要选择一个好的函数,使得p最大。
我们需要一种采样分布,它能让对手对使用哪个点作为分叉漠不关心。否则,查询就会浪费在一个最佳对手无论如何也不会使之无效的区块上。
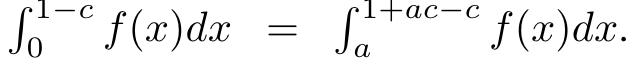
这样一个概率密度函数使得,对手在初始位置和任一位置进行分叉时,我们捕获他们的概率相同
那么可以推导得到
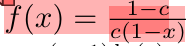
将函数归一化,并且由于积分到1是无穷,因此只积分到 1 − δ 1-\delta 1−δ ,最后 δ \delta δ 比例的区块,我们直接采样。
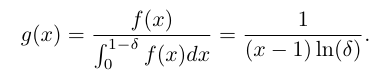
p
=
log
δ
(
c
)
p = \log_\delta(c)
p=logδ(c)
经过计算,如果要满足安全,需要查询的区块的数量仅仅需要 log n 级
同样,当面对难度可变的情况时,还是使用相同的概率函数,但是x 从区块长度的概念转换到了区块难度的概念。
能够记录每个区块的相对难度,还要对MMR进行改造
每个节点都有 h , w , t , D s t a r t , D n e x t , n , d a t a h, w, t, D_{start}, D_{next}, n, data h,w,t,Dstart,Dnext,n,data ,
- w是总难度
- h 是哈希
- t 时间戳
- D 是难度目标,D_start 是当前块的难度, D_dest 是根据函数计算得到的下一区块的难度
- n 是子树大小
- data 可以填充任意字符串

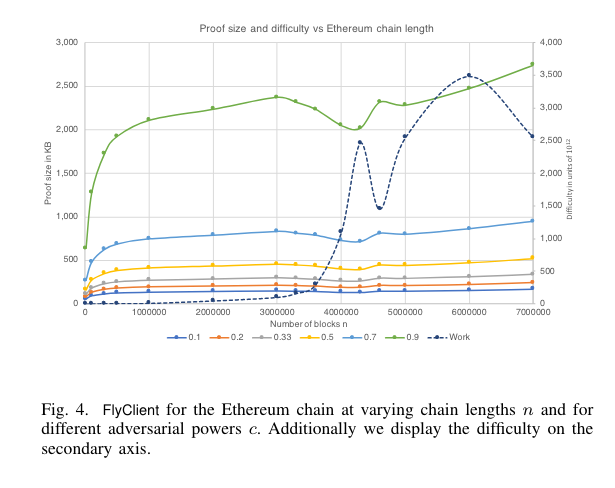
实验
由于对于区块头的验证速度非常快,都是不需要1s就能验证,因此主要比较的就是验证需要的数据量的多少。