AVL树的基本概念

AVL树的平衡因子、

AVL树的旋转

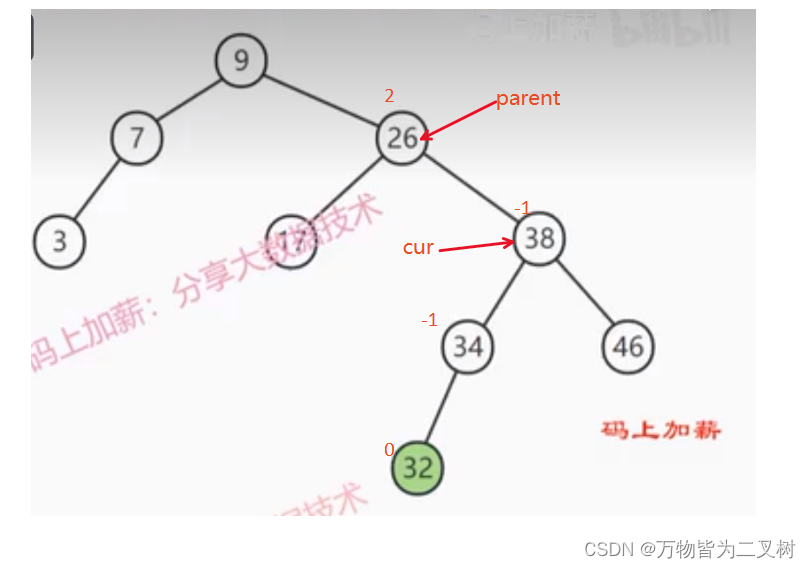
当平衡因子的高度差过大时，就要选择。所谓的选择其实也是一种压扁的操作

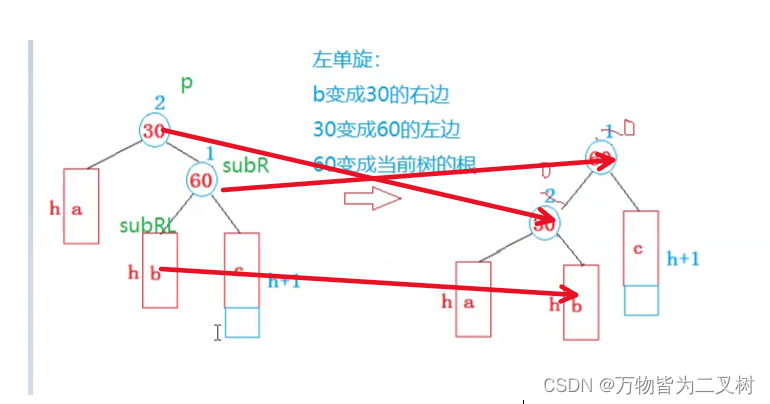
在本例中 新插入的蓝色结点使得不在平衡。

我们看上图就能得出 这就是左单旋，左单旋就是把左边压下去，这样左右就一样高了。
左单旋代码演示：
接下来 我们给结点命名

根据结点名称变化关系:
我们看出 parent 和subr在旋转后，parent和subr都获得了平衡，他们的平衡因子都是0。所以我们在旋转之后 parent，subr都获得了平衡。

void Rotatel(Node* parent)
	{
		Node* subR = parent->right;//根据结点命名指出 对应的名字
		Node* subRl = subR->left;
		
		parent->right = subRl;
		if (subRl)
		{
			subRl->parent = parent;
		}
		
		subR->left = parent;
		Node* ppnode = parent->parent;
		parent->parent=subR;

		if (parent == _root)
		{
			_root = subR; 
			subR->parent = nullptr;
		} 
		else
		{
			if (parent == ppnode->right)
			{
				ppnode->right = subR;
			}
			else
			{
				ppnode->left = subR;
			}
			subR->parent = ppnode;
		}
		
		parent->_bf = 0;
		subR->_bf = 0;
	} 

右旋也是一样。

和左旋一样，avl的旋转就可以保持水平。

avl的双旋

avl的双旋以下图为例，先左旋后右旋。

在本例中，左侧二叉树偏高，进行左单旋。 左单旋是将父亲结点的右子树当新的父亲 。

先左单旋，然互右单旋。左单旋是单旋的父亲的左子树，右单旋是对整个树进行单旋。

通过这个图，我们可以大概看出来。90 和60的右子树一起去了右边。30去了左边。平衡之后，只有原来的parent 是1 其他都是0.

Node* subL = parent->left;
		Node* subLR = subL->right;
		int bf = subLR->_bf;
		Rotatel(parent->left);
		Rotater(parent);

选择之后，调节后的平衡因子就很重要。
上图为第一种情况， 插入之后，bf为-1.调节之后达到平衡。此时parent为1 其他都为0。
有一种特殊情况。

双旋之后 每一个结点的平衡因子 都是0.

if (bf == -1)
		{
			parent->_bf == 1;
			subL->_bf = subLR->_bf = 0;
		}
		else if (bf==1)
		{
			subL->_bf = -1;
			parent->_bf = subLR->_bf = 0;
		}
		else if (bf == 0)
		{
			subL->_bf = subLR->_bf = parent->_bf = 0;
		}

具体选择图：

下面我们给一张图：

AVL的双旋的另一种 右左双旋。 右左双旋：

子树右旋之后：

右旋之后整体情况：

这个树是典型的RL形

RL形先右子树右旋 然互左旋

旋转的4种情况

LL的右旋 cur=-1 parent=-2

RR的左旋 cur=-1 parent=-1

LR的双旋 paren=-2 cur=1

RL的双旋 parent==2 cur=-1