导 读

当将模型拟合到数据集时，可能需要执行特征选择：由于多种原因，仅保留某些特征子集来拟合模型，而丢弃其余特征具有一定的必要性，如下：

• 保持模型的可解释性（特征太多会使解释变得更加困难）

• 避免维度过大

• 最大化/最小化与模型相关的一些目标函数（R 平方、AIC 等）

• 以避免不合适等。

有需要的朋友关注公众号【小Z的科研日常】，获取更多内容。

01、协方差矩阵适应进化策略

如果特征数量 N 很小，则可以进行详尽的搜索：可以逐个尝试所有可能的特征组合，并只保留使成本/目标函数最小化的组合。

但如果 N 很大，那么详尽的搜索可能是不可能的。2^N中，如果 N 大于几十，则要尝试的组合种类使计算资源受限（它是一个指数函数）。

在这种情况下，启发式方算法便是很好的解决方案：以有效的方式探索搜索空间，寻找能够最小化用于执行搜索的目标函数的特征组合。

假设我们正在寻找的是长度为 N 的向量[1, 0, 0, 1, 0, 1, 1, 1, 0, ...]，其中元素取值于{0, 1}。向量中的每个元素被分配给一个特征。

如果元素为1，则选择该特征；如果元素为0，则丢弃该特征。我们需要找到最小化目标函数的向量。搜索空间的维度 N 与特征的数量一样多；任何维度上唯一可能的值是 0 和 1。

找到一个好的启发式算法并非易事。scikit-learn 提供了多种方法来执行启发式特征选择，前提是我们的问题非常适合。

但找到一个好的、通用的启发式是一个难题。在本系列文章中，我们将探讨一些即使在 N 很大时也可以解决问题，并且目标函数实际上可以是代码中计算的任何内容。

02、数据集和完整代码

本文中的所有优化方法，使用Kaggle 的房价数据集。经过一些简单的特征转换后，数据最终有 213 个特征 (N=213) 和 1453 个观察值。

我使用的模型是线性回归，并且试图最小化的目标函数是 BIC（贝叶斯信息准则），这是一种信息损失的度量，因此 BIC 越低越好。它类似于 AIC（Akaike 信息准则），但 BIC 倾向于产生更简约的模型：它更喜欢特征较少的模型。

最小化 AIC 或 BIC 往往会减少过度拟合。但也可以使用其他目标函数，例如 R 平方或调整后的 R 平方。

最终，目标函数的选择在这里无关紧要。重要的是我们有一个目标函数，我们一直在尝试使用各种技术来优化它。

我们将尝试通过功能选择来最小化 BIC，因此这是在statsmodels.api.OLS()完成任何功能选择之前的 BIC 的基线值 - 启用所有功能：

baseline BIC: 34570.166173470934

现在让我们开始本文的的特征选择技术。

03、SFS:顺序特征搜索

SFS（前向版本）相当简单。它首先尝试选择单个特征，然后选择最小化目标函数的特征。一旦选择了某个功能，它就会永远保持选中状态。

然后它尝试向其中添加另一个特征（总共 2 个特征），以再次最小化目标。每次尝试找到最佳的新特征以添加到现有集合中时，它都会将所选特征的数量增加 1。

当所有功能一起尝试后，搜索结束。无论哪种组合能够最小化目标，都会获胜。

SFS 是一种贪婪算法——每个选择都是局部最优的——并且它永远不会回去纠正自己的错误。但即使 N 很大，它也相当快。它尝试的组合总数是 N(N+1)/2 一个二次多项式（而穷举搜索需要执行指数次数的尝试）。

让我们使用mlxtend 库看看 Python 中的 SFS 代码是什么样子：

import statsmodels.api as sm
from mlxtend.feature_selection import SequentialFeatureSelector as SFS
from sklearn.base import BaseEstimator

class DummyEstimator(BaseEstimator):
    # mlxtend 希望使用 sklearn ，但这里不需要它
    # (使用统计模型 OLS 代替）。
    def fit(self, X, y=None, **kwargs):
        return self

def neg_bic(m, X, y):
    # 目标函数
    lin_mod_res = sm.OLS(y, X, hasconst=True).fit()
    return -lin_mod_res.bic

seq_selector = SFS(
    DummyEstimator(),
    k_features=(1, X.shape[1]),
    forward=True,
    floating=False,
    scoring=neg_bic,
    cv=None,
    n_jobs=-1,
    verbose=0,
    # 确保拦截不中断
    fixed_features=['const'],
)

n_features = X.shape[1] - 1
objective_runs_sfs = round(n_features * (n_features + 1) / 2)
t_start_seq = time.time()
# 如果不进行 .copy()，mlxtend 会弄乱数据帧。
seq_res = seq_selector.fit(X.copy(), y.copy())
t_end_seq = time.time()
run_time_seq = t_end_seq - t_start_seq
seq_metrics = seq_res.get_metric_dict()

它快速运行组合，下面是总结结果：

best k:         36
best objective: 33708.98602877906
R2 @ best k:    0.9075677543649224
objective runs: 22791
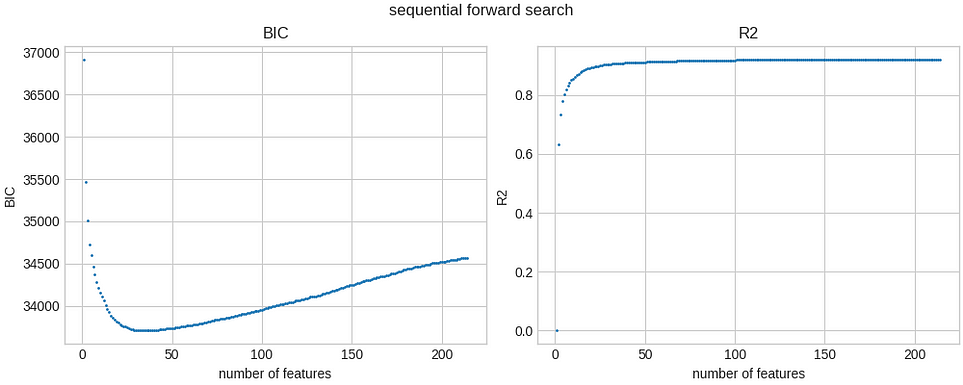
total run time: 42.448 sec

最佳特征数量是 213 个中的 36 个。最佳 BIC 是 33708.986（特征选择之前的基线值为 34570.166），在我的系统上完成需要不到 1 分钟。它调用目标函数 22.8k 次。

这些是最佳 BIC 和 R 平方值，作为所选特征数量的函数：

03、CMA-ES（协方差矩阵适应进化策略）原理

CMA-ES是一种数值优化算法。它与遗传算法属于同一类（它们都是进化算法），但 CMA-ES 与 GA 截然不同。该算法是随机的，不需要计算目标函数的导数（与依赖于偏导数的梯度下降不同）。

它的计算效率很高，并且用于各种数值优化库（例如 Optuna）。我在这里仅尝试对 CMA-ES 进行简要概述。

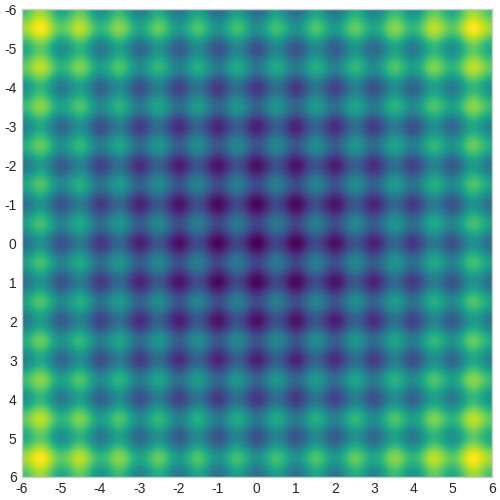
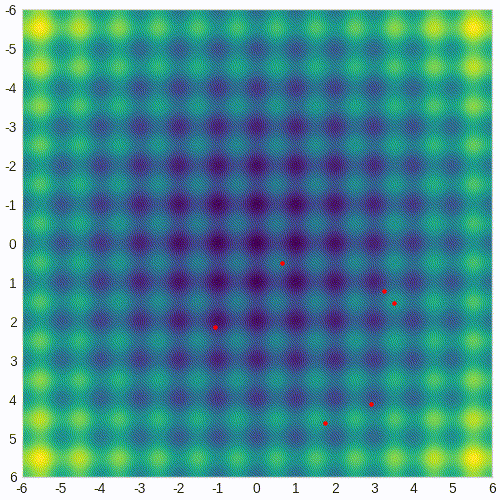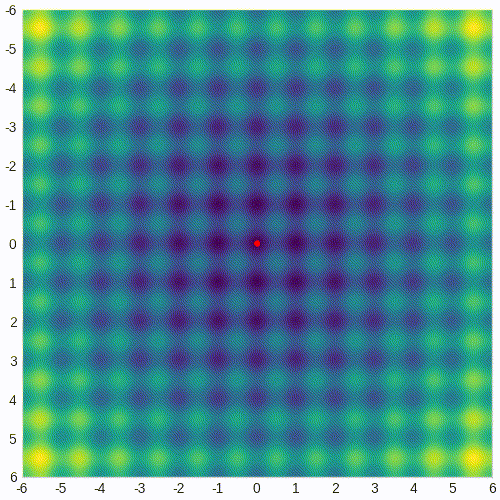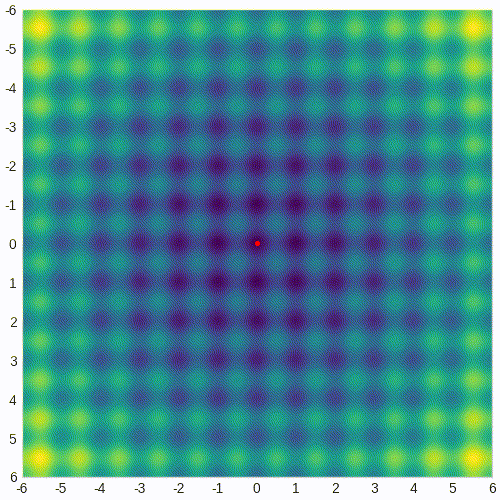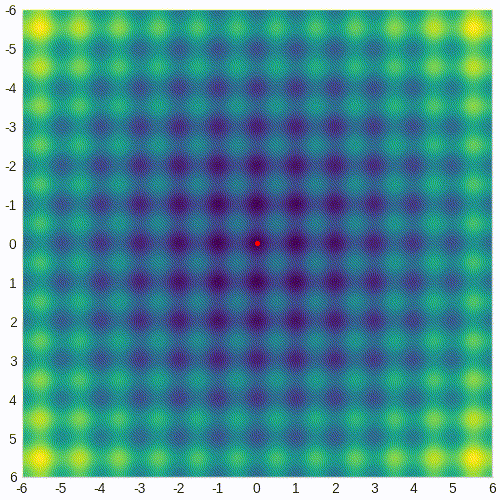
考虑二维 Rastrigin 函数：

下面的热图显示了该函数的值（颜色越亮意味着值越高）。该函数在原点 (0, 0) 处具有全局最小值，但也充满了许多局部极值。我们需要通过 CMA-ES 找到全局最小值。

CMA-ES是基于多元正态分布。它根据该分布在搜索空间中生成测试点。我们需要初始化分布的原始平均值及其标准差，但之后算法将迭代修改所有这些参数，在搜索空间中扫描分布，寻找最佳目标函数值。这是测试点的原始分布：

xi是算法在搜索空间中每一步生成的点集。lambda是生成的点数。分布的平均值将在每一步中更新，并希望最终收敛于真正的解决方案。sigma是分布的标准差——测试点的分布。

C是协方差矩阵：它定义分布的形状。根据C分布的值，可能具有“圆形”形状或更细长的椭圆形形状。进行更改以C允许 CMA-ES“潜入”搜索空间中的某些区域，或避开其他区域。

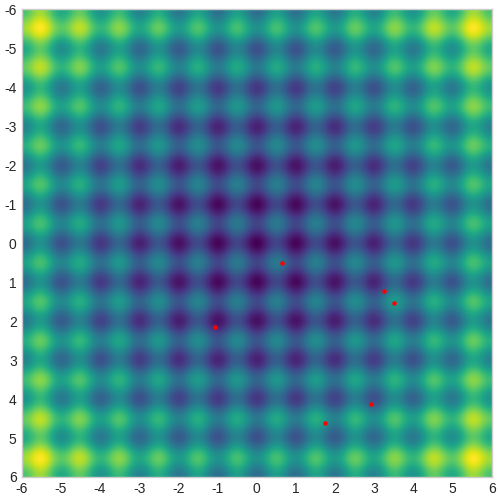
上图中生成了 6 个点的总体，这是优化器针对此问题选择的默认总体大小。这是第一步。之后，算法需要：

• 计算每个点的目标函数 (Rastrigin)

• 根据从目标函数中学到的知识，更新均值、标准差和协方差矩阵，有效地创建新的多元正态分布

• 从新分布生成一组新的测试点

• 重复直到满足某些标准（收敛于某个平均值，或超过最大步数等）

由于篇幅限制，本文将不展示所有分布参数的更新。但仅更新分布的平均值非常简单，其工作原理如下：计算每个测试点的目标函数后，为这些点分配权重，目标值更好的点赋予较大的权重，并根据它们的位置计算加权和，这成为新的平均值。实际上，CMA-ES 将分布平均值移向具有更好目标值的点：

如果算法收敛到真实解，则分布的平均值将收敛到该解。标准差将收敛到 0。协方差矩阵将根据目标函数的地理位置改变分布的形状（圆形或椭圆形），扩展到有希望的区域，并避开不良区域。

这是一个动画 GIF，显示了 CMA-ES 解决 Rastrigin 问题时测试点随时间的演变：

04、CMA-ES（协方差矩阵适应进化策略）代码

2D Rastrigin 函数相对简单，因为它只有 2 维。对于我们的特征选择问题，我们有 N=213 维。而且，空间并不是连续的。每个测试点都是一个 N 维向量，其分量值来自{0, 1}。

换句话说，每个测试点看起来像这样：[1, 0, 0, 1, 1, 1, 0, ...]— 一个二进制向量。但除此之外，问题是相同的：我们需要找到最小化目标函数的点（或向量）：OLS 模型的 BIC 参数。

以下是使用cmaes 库进行特征选择的 CMA-ES 代码的简单版本：

def cma_objective(fs):
    features_use = ['const'] + [
        f for i, f in enumerate(features_select) if fs[i,] == 1
    ]
    lin_mod = sm.OLS(y_cmaes, X_cmaes[features_use], hasconst=True).fit()
    return lin_mod.bic


X_cmaes = X.copy()
y_cmaes = y.copy()
features_select = [f for f in X_cmaes.columns if f != 'const']

dim = len(features_select)
bounds = np.tile([0, 1], (dim, 1))
steps = np.ones(dim)
optimizer = CMAwM(
    mean=np.full(dim, 0.5),
    sigma=1 / 6,
    bounds=bounds,
    steps=steps,
    n_max_resampling=10 * dim,
    seed=0,
)

max_gen = 100
best_objective_cmaes_small = np.inf
best_sol_raw_cmaes_small = None
for gen in tqdm(range(max_gen)):
    solutions = []
    for _ in range(optimizer.population_size):
        x_for_eval, x_for_tell = optimizer.ask()
        value = cma_objective(x_for_eval)
        solutions.append((x_for_tell, value))
        if value < best_objective_cmaes_small:
            best_objective_cmaes_small = value
            best_sol_raw_cmaes_small = x_for_eval
    optimizer.tell(solutions)

best_features_cmaes_small = [
    features_select[i]
    for i, val in enumerate(best_sol_raw_cmaes_small.tolist())
    if val == 1.0
]
print(f'best objective: {best_objective_cmaes_small}')
print(f'best features:  {best_features_cmaes_small}')

CMA-ES 优化器是通过对平均值和 sigma（标准差）的一些初始猜测来定义的。然后它会循环很多代，创建测试点x_for_eval，用目标评估它们，修改分布（均值、西格玛、协方差矩阵）等。每个x_for_eval点都是一个二进制向量，[1, 1, 1, 0, 0, 1, ...]用于从数据集中选择特征。

请注意，优化器使用的是CMAWM()而不是默认的CMA()。默认优化器对于常规的连续问题效果很好，但这里的搜索空间是高维的，并且只允许两个离散值（0 和 1）。默认优化器陷入了这个空间。CMAwM()扩大了一点搜索空间（虽然它返回的解决方案仍然是二进制向量）。

这些是优化的 CMA-ES 代码的主要统计数据：

最佳目标：33703.070530508514
最佳生成：921
目标运行：20000
最佳时间：48.326 秒

它能够找到比 SFS 更好（更小）的目标值，它调用目标函数的次数更少（20k），并且花费的时间大约相同。从所有指标来看，这都是相对于 SFS 的净收益。