wy的leetcode刷题记录_Day82

news2024/10/6 6:03:44

wy的leetcode刷题记录_Day82

声明

本文章的所有题目信息都来源于leetcode
如有侵权请联系我删掉!
时间：2024-3-6

前言

目录

  • wy的leetcode刷题记录_Day82
    • 声明
    • 前言
    • 2917. 找出数组中的 K-or 值
      • 题目介绍
      • 思路
      • 代码
      • 收获
    • 143. 重排链表
      • 题目介绍
      • 思路
      • 代码
      • 收获
    • 146. LRU 缓存
      • 题目介绍
      • 思路
      • 代码
      • 收获
    • 147. 对链表进行插入排序
      • 题目介绍
      • 思路
      • 代码
      • 收获
    • 160. 相交链表
      • 题目介绍
      • 思路
      • 代码
      • 收获
    • 203. 移除链表元素
      • 题目介绍
      • 思路
      • 代码
      • 收获

2917. 找出数组中的 K-or 值

今天的每日一题是：2917. 找出数组中的 K-or 值

题目介绍

给你一个下标从 0 开始的整数数组 nums 和一个整数 k 。

nums 中的 K-or 是一个满足以下条件的非负整数：

  • 只有在 nums 中，至少存在 k 个元素的第 i 位值为 1 ，那么 K-or 中的第 i 位的值才是 1 。

返回 nums 的 K-or 值。

注意 ：对于整数 x ，如果 (2i AND x) == 2i ，则 x 中的第 i 位值为 1 ，其中 AND 为按位与运算符。

示例 1：

输入：nums = [7,12,9,8,9,15], k = 4
输出：9
解释：nums[0]、nums[2]、nums[4] 和nums[5] 的第 0 位的值为 1 。
nums[0] 和 nums[5] 的第 1 位的值为 1 。
nums[0]、nums[1]和 nums[5] 的第 2 位的值为 1 。
nums[1]、nums[2]、nums[3]、nums[4] 和 nums[5] 的第 3 位的值为 1 。
只有第 0 位和第 3 位满足数组中至少存在 k 个元素在对应位上的值为 1 。
因此，答案为 2^0 + 2^3 = 9。

示例 2：
输入：nums = [2,12,1,11,4,5], k = 6
输出：0
解释：因为 k == 6 == nums.length，所以数组的 6-or 等于其中所有元素按位与运算的结果。
因此，答案为 2 AND 12 AND 1 AND 11 AND 4 AND 5= 0 。

示例 3：

输入：nums = [10,8,5,9,11,6,8], k = 1
输出：15
解释：因为 k == 1 ，数组的 1-or等于其中所有元素按位或运算的结果。因此，答案为 10 OR 8 OR 5 OR 9 OR 11 OR 6 OR 8 = 15 。

思路

简单的模拟枚举：首先简历一个长度为32哈希表count（对应32位数），然后遍历nums，统计每一个num的二进制位然后count对应的二进制位自增，最后遍历count中的值与k的值计算得出答案。

代码

class Solution {
public:
    int findKOr(vector<int>& nums, int k) {
        int n=nums.size();
        vector<int> count(32,0);
        int ans=0;

        for(auto num:nums)
        {
            int i=0;
            while(num!=0)
            {
                if(num&1==1)
                {
                    count[i]++;
                }
                i++;
                num=num>>1;
            }
        }
        for(int i=0;i<32;i++)
        {
            if(count[i]>=k)
            {
                ans+=1<<i;
            }
        }
        return ans;
    }
};

收获

对于整数 x ，如果 (2i AND x) == 2i ，则 x 中的第 i 位值为 1 ，其中 AND 为按位与运算符。快速判断二进制位。

143. 重排链表

143. 重排链表

题目介绍

给定一个单链表 L 的头节点 head ，单链表 L 表示为：

L0 → L1 → … → Ln - 1 → Ln

请将其重新排列后变为：

L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …

不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。

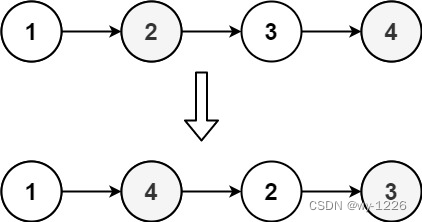
示例 1：
在这里插入图片描述
输入：head = [1,2,3,4]
输出：[1,4,2,3]

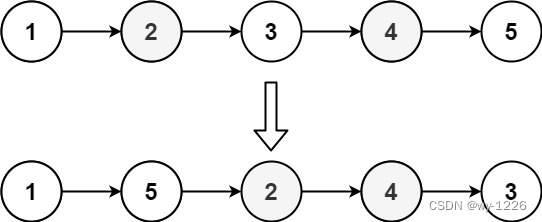
示例 2：
在这里插入图片描述
输入：head = [1,2,3,4,5]
输出：[1,5,2,4,3]

思路

我的想法是，将链表拆成前半段和后半段，然后反转后半段链表，最后将这俩个链表拼接起来即可。反转链表在前几天已经做了几次了这里就不多说，拆分链表的话也是用我们的老朋友快慢指针，慢指针走一步快指针走两步，当快指针走到尾部时，慢指针刚好处于链表中间，将链表分为两部分。

代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverse(ListNode* head)
    {
        ListNode* pre=nullptr;
        ListNode* cur=head;
        while(cur)
        {
            ListNode* temp=cur->next;

            cur->next=pre;
            pre=cur;
            cur=temp;
        }
        return pre;
    }

    void reorderList(ListNode* head) {
        ListNode* slow=head;
        ListNode* fast=head;
        while(fast->next!=nullptr&&fast->next->next!=nullptr)
        {
            slow=slow->next;
            fast=fast->next->next;
        }

        ListNode* newHead=slow->next;
        slow->next=nullptr;
        newHead=reverse(newHead);

        while(newHead)
        {
            ListNode* temp=newHead->next;
            newHead->next=head->next;
            head->next=newHead;
            head=newHead->next;
            newHead=temp;
        }

    }
};

收获

无

146. LRU 缓存

146. LRU 缓存

题目介绍

请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。
实现 LRUCache 类：

  • LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
  • int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
  • void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该 逐出 最久未使用的关键字。

函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

示例：

输入:
[“LRUCache”, “put”, “put”, “get”, “put”, “get”, “put”, “get”, “get”, “get”]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出:
[null, null, null, 1, null, -1, null, -1, 3, 4]

解释 :
LRUCache lRUCache = new LRUCache(2); lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 4

思路

本题需要维护一个队列，俩个哈希表。一个int变量sum用来保存当前队列中不同元素的个数，队列Q用来记录在超出缓存之前进行get和put操作的元素key值，哈希表count用来记录某一个元素get和put操作的次数，哈希表val表示kv关系。每次替换发生的时机在put一个元素并进行检查时sum>capacity，这个时候我们需要对队列进行清空，每弹出一个元素则需要对应count[key]递减，直到某一个key的count变为0说明他最近用的少，最后用新元素替换该key。

代码

class LRUCache {
public:
const int maxn = 2e5 + 5;
    queue<int> Q;
    vector<int> count,val;
    int sum=0,cap=0;

    LRUCache(int capacity) {
        cap=capacity;
        count=vector(maxn,0);
        val=vector(maxn,0);
    }
    
    int get(int key) {
        if(count[key]>0)
        {
            count[key]++;
            Q.push(key);
            return val[key];
        }
        else
        {
            return -1;
        }
    }
    
    void put(int key, int value) {
        if(count[key]==0) sum++;
        val[key]=value;
        
        Q.push(key);
        count[key]++;
        
        if(sum>cap)
        {
            while(1)
            {
                int temp=Q.front();
                Q.pop();
                if(--count[temp]==0)
                {
                    sum--;
                    break;
                }
            }
        }

    }
};

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache* obj = new LRUCache(capacity);
 * int param_1 = obj->get(key);
 * obj->put(key,value);
 */

收获

很难，这题看别人的思路才写得出来，而且很多bug，耗费时间也很长，希望二刷的时候能真正自己快速写出来。

147. 对链表进行插入排序

147. 对链表进行插入排序

题目介绍

给定单个链表的头 head ，使用 插入排序 对链表进行排序，并返回 排序后链表的头 。

插入排序 算法的步骤:

  • 1.插入排序是迭代的，每次只移动一个元素，直到所有元素可以形成一个有序的输出列表。
  • 2.每次迭代中，插入排序只从输入数据中移除一个待排序的元素，找到它在序列中适当的位置，并将其插入。
  • 3.重复直到所有输入数据插入完为止。

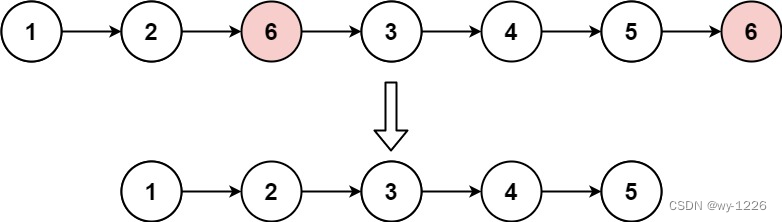
下面是插入排序算法的一个图形示例。部分排序的列表(黑色)最初只包含列表中的第一个元素。每次迭代时，从输入数据中删除一个元素(红色)，并就地插入已排序的列表中。

对链表进行插入排序。

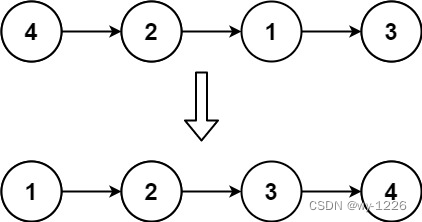
示例 1：

在这里插入图片描述

输入: head = [4,2,1,3]
输出: [1,2,3,4]

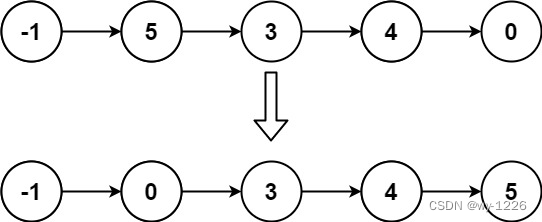
示例 2：

在这里插入图片描述

输入: head = [-1,5,3,4,0]
输出: [-1,0,3,4,5]

思路

相信大家都一定了解插入排序，类似抽牌一样，每次插入前都是有序的数列保证插入后也是有序的数列。根据这个理念我们来实现具体细节，其中我们需要一个哑节点来保证能返回原来的链表（因为头节点可能发生变化），其次我们需要一个节点temp来保存当前排序到的位置，即temp前排序完成，temp后待排序。然后在temp后进行搜寻的时候我们同样需要一个pre和一个cur来将选中节点从原链表中取出最终拆入到temp后面即可。

代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* insertionSortList(ListNode* head) {
        ListNode *dummy=new ListNode(0,head);
        ListNode *temp=dummy;
        int n=0;
        while(head)
        {
            head=head->next;
            n++;
        }
        for(int i=0;i<n-1;i++)
        {
            ListNode* pre=temp;
            if(temp->next==nullptr)
                break;
            head=temp->next;
            int minVal=head->val;
            while(head)
            {
                minVal=min(minVal,head->val);
                head=head->next;
            }

            head=temp->next;

            while(head)
            { 
                if(head->val==minVal)
                {
                    pre->next=head->next;
                    head->next=temp->next;
                    temp->next=head;
                    break;
                }
                pre=head;
                head=head->next;
            }
            temp=temp->next;
        }
        return dummy->next;
    }
};

收获

熟练了链表的操作，温故了插入排序。

160. 相交链表

160. 相交链表

题目介绍

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

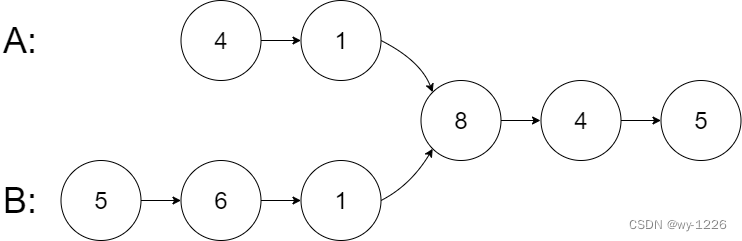
图示两个链表在节点 c1 开始相交：

在这里插入图片描述

题目数据 保证 整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

自定义评测：

评测系统 的输入如下（你设计的程序 不适用 此输入）：

  • intersectVal - 相交的起始节点的值。如果不存在相交节点，这一值为 0
  • listA - 第一个链表
  • listB - 第二个链表
  • skipA - 在 listA 中（从头节点开始）跳到交叉节点的节点数
  • skipB - 在 listB 中（从头节点开始）跳到交叉节点的节点数

评测系统将根据这些输入创建链式数据结构，并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点，那么你的解决方案将被 视作正确答案 。

示例 1：

在这里插入图片描述

输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA= 2, skipB = 3
输出：Intersected at ‘8’
解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。 从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,6,1,8,4,5]。 在 A 中，相交节点前有 2个节点；在 B 中，相交节点前有 3 个节点。 — 请注意相交节点的值不为 1，因为在链表 A 和链表 B 之中值为 1 的节点 (A中第二个节点和 B 中第三个节点) 是不同的节点。换句话说，它们在内存中指向两个不同的位置，而链表 A 和链表 B 中值为 8 的节点 (A中第三个节点，B 中第四个节点) 在内存中指向相同的位置。

示例 2：

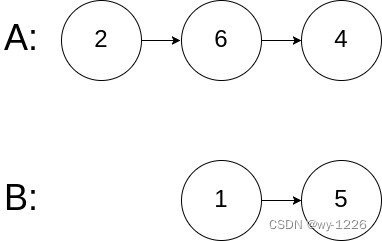
在这里插入图片描述

输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出：null
解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。 由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。 这两个链表不相交，因此返回 null 。

思路

我直接用傻瓜做法：计算俩个链表的长度之差c，让较长的链表先遍历c步，然后同时遍历两个链表判断是否指向同一个节点即可。

代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        int a=0,b=0;
        ListNode* temp=headA;
        while(temp)
        {
            a++;
            temp=temp->next;
        }
        temp=headB;
        while(temp)
        {
            b++;
            temp=temp->next;
        }
        int c=abs(b-a);
        if(b>a)
        {
            while(c--)
            {
                headB=headB->next;
            }
        }
        else
        {
            while(c--)
            {
                headA=headA->next;
            }
        }
        while(headA!=headB&&headA!=nullptr)
        {
            headA=headA->next;
            headB=headB->next;
        }
        if(headA)
            return headA;
        return nullptr;
        
    }
};

收获

无

203. 移除链表元素

203. 移除链表元素

题目介绍

给你一个链表的头节点 head 和一个整数 val ，请你删除链表中所有满足 Node.val == val 的节点，并返回 新的头节点 。

示例 1：
在这里插入图片描述
输入：head = [1,2,6,3,4,5,6], val = 6
输出：[1,2,3,4,5]

示例 2：

输入：head = [], val = 1
输出：[]

示例 3：

输入：head = [7,7,7,7], val = 7
输出：[]

思路

双指针，一个指针用来遍历，另一个指针用来保存遍历节点的上一个节点以方便进行删除。

代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        ListNode* dummy=new ListNode(-1,head);
        ListNode* pre=dummy;
        while(head)
        {
            if(head->val==val)
            {
                pre->next=head->next;
                head=head->next;
            }
            else
            {
                pre=head;
                head=head->next;
            }

        }
        return dummy->next;
    }
};

收获

无

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1493810.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【C/C++】结构体内存对齐 ----- 面试必考（超详细解析，小白一看就懂！！！）

【C/C++】结构体内存对齐 ----- 面试必考（超详细解析，小白一看就懂！！！）

目录 一、前言 二、引出 ---- 结构体内存对齐 &#x1f34e;结构体偏移量计算&#xff1a;offsetof &#x1f95d;结构体内存对齐详解 &#x1f4a6;规则介绍&#xff08;重点&#xff01;&#xff01;&#xff09; &#x1f4a6;例题解析 三、习题演练 &#x1f34d;练习① …
阅读更多...
Vue.js+SpringBoot开发森林火灾预警系统

Vue.js+SpringBoot开发森林火灾预警系统

目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 数据中心模块2.2 系统基础模块2.3 烟雾传感器模块2.4 温度传感器模块2.5 历史记录模块2.6 园区数据模块 三、系统设计3.1 用例设计3.1.1 森林园区基础系统用例设计3.1.2 森林预警数据用例设计 3.2 数据库设计3.2.1 烟雾…
阅读更多...
JAVA毕业设计633—基于Java+ssm的医院挂号系统(源代码+数据库+11000字论文+开题)

JAVA毕业设计633—基于Java+ssm的医院挂号系统(源代码+数据库+11000字论文+开题)

毕设所有选题&#xff1a; https://blog.csdn.net/2303_76227485/article/details/131104075 基于Javassm的医院挂号系统(源代码数据库11000字论文开题)633 一、系统介绍 本系统分为管理员、医生、用户三种角色 1、用户&#xff1a; 注册、登录、医生预约、评价、收藏、健…
阅读更多...
【EI会议征稿通知】第四届人工智能，大数据与算法国际学术会议 (CAIBDA 2024)

【EI会议征稿通知】第四届人工智能，大数据与算法国际学术会议 (CAIBDA 2024)

第四届人工智能&#xff0c;大数据与算法国际学术会议 (CAIBDA 2024) 2024 4th International Conference on Artificial Intelligence, Big Data and Algorithms 由河南省科学院、河南大学主办&#xff0c;河南省科学院智慧创制研究所、河南大学学术发展部、河南大学人工智能…
阅读更多...
循环神经网络（RNN）算法详解

循环神经网络（RNN）算法详解

注意&#xff1a;本文引用自专业人工智能社区Venus AI 更多AI知识请参考原站 &#xff08;[www.aideeplearning.cn]&#xff09; 引言 在之前的博文中&#xff0c;我们探讨了全连接神经网络&#xff08;FCNN&#xff09;和卷积神经网络&#xff08;CNN&#xff09;的结构&am…
阅读更多...
C及C++每日练习(2)

C及C++每日练习(2)

1.选择&#xff1a; 1.使用printf函数打印一个double类型的数据&#xff0c;要求&#xff1a;输出为10进制&#xff0c;输出左对齐30个字符&#xff0c;4位精度。以下哪个选项是正确的&#xff1f; A.%-30.4e B.%4.30e C.%-30.4f D.%-4.30 在上一篇文章中&#xff0c;提到了…
阅读更多...
Miniconda3迁移(附图详细过程)

Miniconda3迁移(附图详细过程)

背景&#xff1a; 磁盘占满了&#xff0c;本来根目录下是100%&#xff0c;所以想着将conda的环境换个大点的盘&#xff0c;我这里是将miniconda3从[ / ]移到了[ /data1 ] 解决方法&#xff1a; 1.首先停止所有与miniconda相关进程 conda deactivate2.移动miniconda到新的目…
阅读更多...
微信小程序开发系列（七）·如何实现小程序页面的快速跳转、小程序样式·尺寸单位rpx以及全局样式和局部样式的区别

微信小程序开发系列（七）·如何实现小程序页面的快速跳转、小程序样式·尺寸单位rpx以及全局样式和局部样式的区别

微信小程序开发_时光の尘的博客-CSDN博客 目录 1. 小程序样式和组件介绍 2. 如何实现页面的快速跳转 3. 小程序样式尺寸单位rpx 3.1 使用px 3.2 使用rpx 4. 全局样式和局部样式 4.1 全局样式 4.2 局部样式 1. 小程序样式和组件介绍 在开发 Web网站的时候&am…
阅读更多...
【学习笔记】卫星基础知识

【学习笔记】卫星基础知识

一、什么是卫星以及它如何工作&#xff1f; 通信卫星是一种人造卫星&#xff0c;通过使用转发器在源和接收器之间中继和放大无线电电信信号。卫星的工作原理是接收从地球发送的无线电信号并将无线电信号重新发送回地球。卫星使用从大型太阳能电池阵列收集的太阳能&#xff0c;…
阅读更多...
利用axios库在Node.js中进行代理请求的实践

利用axios库在Node.js中进行代理请求的实践

前言 随着互联网的蓬勃发展&#xff0c;Web应用程序越来越依赖于从外部服务器获取数据。在这个过程中&#xff0c;我们经常需要通过代理服务器来访问外部资源。本文将介绍如何充分利用axios库&#xff0c;在Node.js中进行代理请求的最佳实践&#xff0c;并通过一个实际案例来展…
阅读更多...
安防视频监控系统EasyCVR新版本支持用浏览器直接播放视频流

安防视频监控系统EasyCVR新版本支持用浏览器直接播放视频流

智慧安防视频监控平台EasyCVR能在复杂的网络环境中&#xff08;专网、局域网、广域网、VPN、公网等&#xff09;将前端海量的设备进行统一集中接入与视频汇聚管理。平台支持设备通过4G、5G、WIFI、有线等方式进行视频流的快捷传输&#xff0c;支持对外分发多格式的视频流&#…
阅读更多...
【计算机考研择校】四川大学vs电子科技大学哪个难度更大？

【计算机考研择校】四川大学vs电子科技大学哪个难度更大？

川大在文科&#xff0c;经管方面比科大强&#xff0c;医学在国内都很强。但工科方面特别是电子信息领域明显是科大强于川大。毕竟一个是综合大学&#xff0c;一个是工科大学不可同日而语。 就业上&#xff0c;电子科大在IT领域的社会声誉口碑不错。就业一向都很好。这个多问问…
阅读更多...
AES加密学习

AES加密学习

AES&#xff08;高级加密标准&#xff09;是一种对称密钥加密算法&#xff0c;用于加密和解密数据。它被广泛应用于各种安全领域&#xff0c;包括但不限于网络通信、数据存储和软件保护。 历史背景 AES是由比利时密码学家Joan Daemen和Vincent Rijmen设计的Rijndael算法演变而…
阅读更多...
【YOLO v5 v7 v8 v9小目标改进】新CNN架构 InceptionNeXt：怎么让大卷积核既好用又快

【YOLO v5 v7 v8 v9小目标改进】新CNN架构 InceptionNeXt：怎么让大卷积核既好用又快

新CNN架构 InceptionNeXt&#xff1a;怎么让大卷积核既好用又快 提出背景问题: 如何提高大核心卷积的效率&#xff0c;同时保持或提升模型性能&#xff1f; 改进思路MetaNeXtInception深度卷积InceptionNeXt 小目标涨点YOLO v5 魔改YOLO v7 魔改YOLO v8 魔改YOLO v9 魔改 提出背…
阅读更多...
EC600模块通过AT指令接入阿里云物联网平台并发布属性

EC600模块通过AT指令接入阿里云物联网平台并发布属性

摘要&#xff1a;本文介绍一下如何通过EC600模块的AT指令&#xff0c;将设备属性值发送到阿里云物联网平台的方法。 这个模块供电可以是 5-16V 和电脑通过USB串口连接&#xff0c;4线即可。未来集成到自己的系统中的时候&#xff0c;可以直接发送指令即可。 使用的软件是FreeAT…
阅读更多...
Apache ECharts数据可视化技术

Apache ECharts数据可视化技术

介绍 官方地址:Apache ECharts 快速入门案例echarts.init //初始化方法 <!DOCTYPE html> <html><head><meta charset"utf-8" /><title>ECharts</title><!-- 引入刚刚下载的 ECharts 文件 --><script src"echart…
阅读更多...
4.Rust中的所有权（Rust成名绝技）

4.Rust中的所有权（Rust成名绝技）

Rust成名绝技 Rust 之所以能成为万众瞩目的语言&#xff0c;就是因为其内存安全性。在以往&#xff0c;内存安全几乎都是通过 GC 的方式实现&#xff0c;但是 GC 会引来性能、内存占用以及全停顿等问题&#xff0c;在高性能场景、实时性要求高和系统编程上是不可接受的&#x…
阅读更多...
代码随想录-贪心算法

代码随想录-贪心算法

贪心的本质是选择每一阶段的局部最优&#xff0c;从而达到全局最优。 455. 分发饼干 class Solution {public int findContentChildren(int[] g, int[] s) {Arrays.sort(g);Arrays.sort(s);int count 0;int sIndex s.length - 1;for (int i g.length - 1; i > 0; i--) …
阅读更多...
Mamba模型底层技术详解，与Transformer到底有何不同？

Mamba模型底层技术详解，与Transformer到底有何不同？

导读&#xff1a; 基于状态空间模型&#xff08;State Space Model&#xff09;的Mamba模型最近在深度学习领域有赶超Transformer的势头。其最主要的优势就在于其在长序列任务上的优异性能与较低的计算复杂度。本文就Mamba模型的原理进行解析&#xff0c;分析Mamba模型在结构上…
阅读更多...
Dynamo初学常识梳理（四）——Revit图元

Dynamo初学常识梳理（四）——Revit图元

希望想学 Dynamo 的小伙伴坚持住&#xff0c;每天积累一点点知识&#xff0c;Dynamo 你很快就能上手的&#xff01;Dynamo 并不是你想的那样难学哦&#xff01; 今天要讲的是如何从 Dynamo 中获取 Revit 的图元&#xff0c;这些节点很常用&#xff0c;不需要全背下来&#xff0…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023