1.图论基础概念
概念
(注意连通非连通情况,+1节点)
无向图: 度是边的两倍(没有入度和出度的概念)
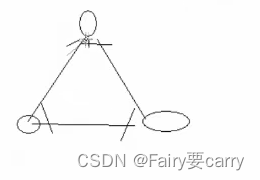
1.完全图: 假设一个图有n个节点,那么任意两个节点都有边则为完全图
2.连通图:是指任意两个结点之间都有一个路径相连。
3.区别: n个顶点的完全图有n(n-1)/2条边;而连通图则不一定,但至少有n-1条边。举个例子,四个顶点的完全图有6条边,也就是四条边加上2条对角线;而连通图可以只包含周围四条边就可以了。
4.强连通图:
你到我有路径,我到你有路径——>最少边数为n(环),至多边数为n(n-1);
有向图G中,如果两个顶点vi,vj间(vi>vj)有一条从vi到vj的有向路径,同时还有一条从vj到vi的有向路径,则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通,称G是一个强连通图。
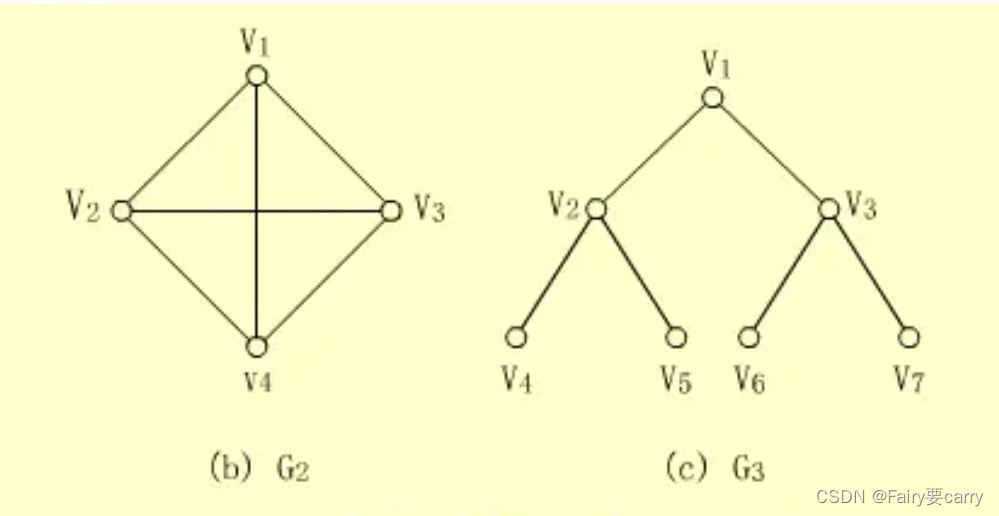
5.连通分量:
- 子图相通
- 子图极大
与连通图对应,一般书上说的都是特指无向图!!
首先要知道分量,分量其实就是子图,只不过说的高大尚罢了。但连通分量不是简单的子图连通,他还除了要求子图连通,还要求该连通子图极大。说白了,无向图极大连通子图就是连通分量。到这里先往下看极大连通子图再回来看

6.极大连通分量:
从5我们知道他首先是连通子图,并且该连通子图是极大的,主要是这里的极大很不好理解。这里我画图举例

7.极小连通分量:

7.生成树:
连通图的生成树是包含图中全部顶点的一个极小连通子图。

8.生成森林:
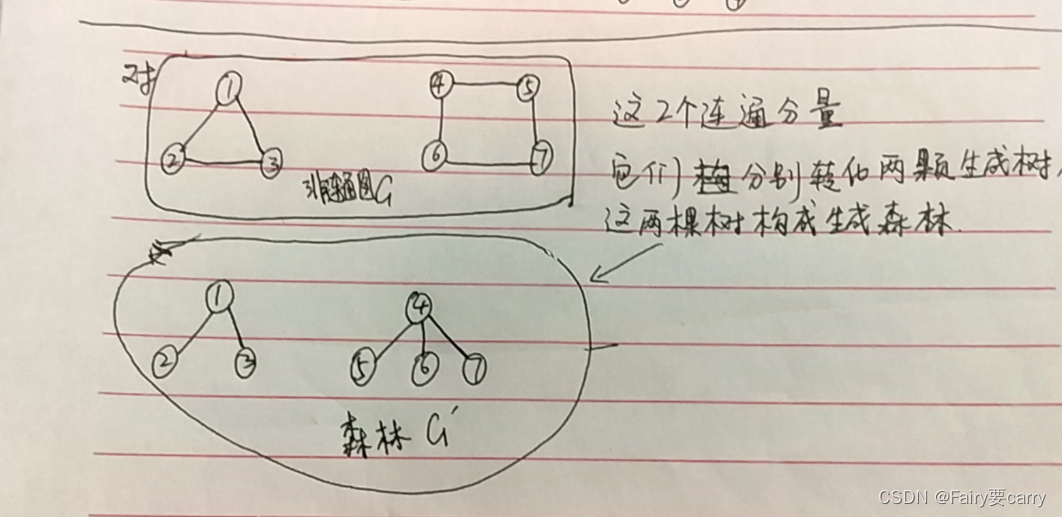
9.有向树
一个顶点的入度为0,其余顶点入度为1的有向图为有向树
例题
1.

2.
答案选B:
无向图:是没有方向的,而强连通图 强调的是有方向的图
而有回路,也不一定正确,可能会出现以下情况:访问不到其余节点
而一棵树,只有从根节点出发才能访问所有节点
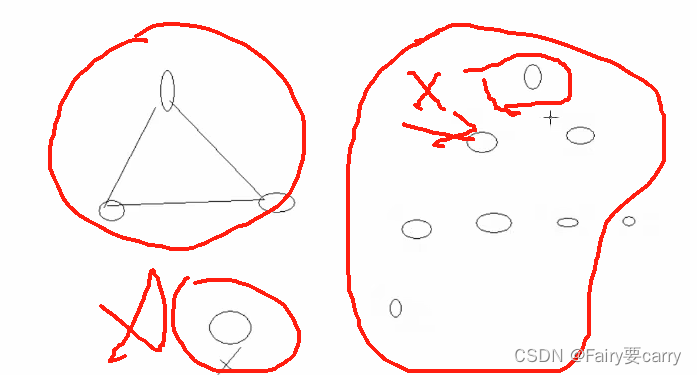

3.
1.子图的概念:
**子图:**假设有两个图G=(V,{E})和g=(v,{e}),如果v⊆V,e⊆E,则称g为G的子图;
例:假设有图G=(V,{E}),顶点集A⊆V,B⊆E,则A和{B}构成G的子图。
答:错误,因为A和B未必能构成图。定义中g是G的子图,是因为给条件时已经明确g是图
2.无向完全图和有向完全图的概念:
无向完全图:每个节点之间都有边,为1/2(n(n-1));
有向完全图:任意两个顶点之间都存在方向相反的两条弧。n(n-1);
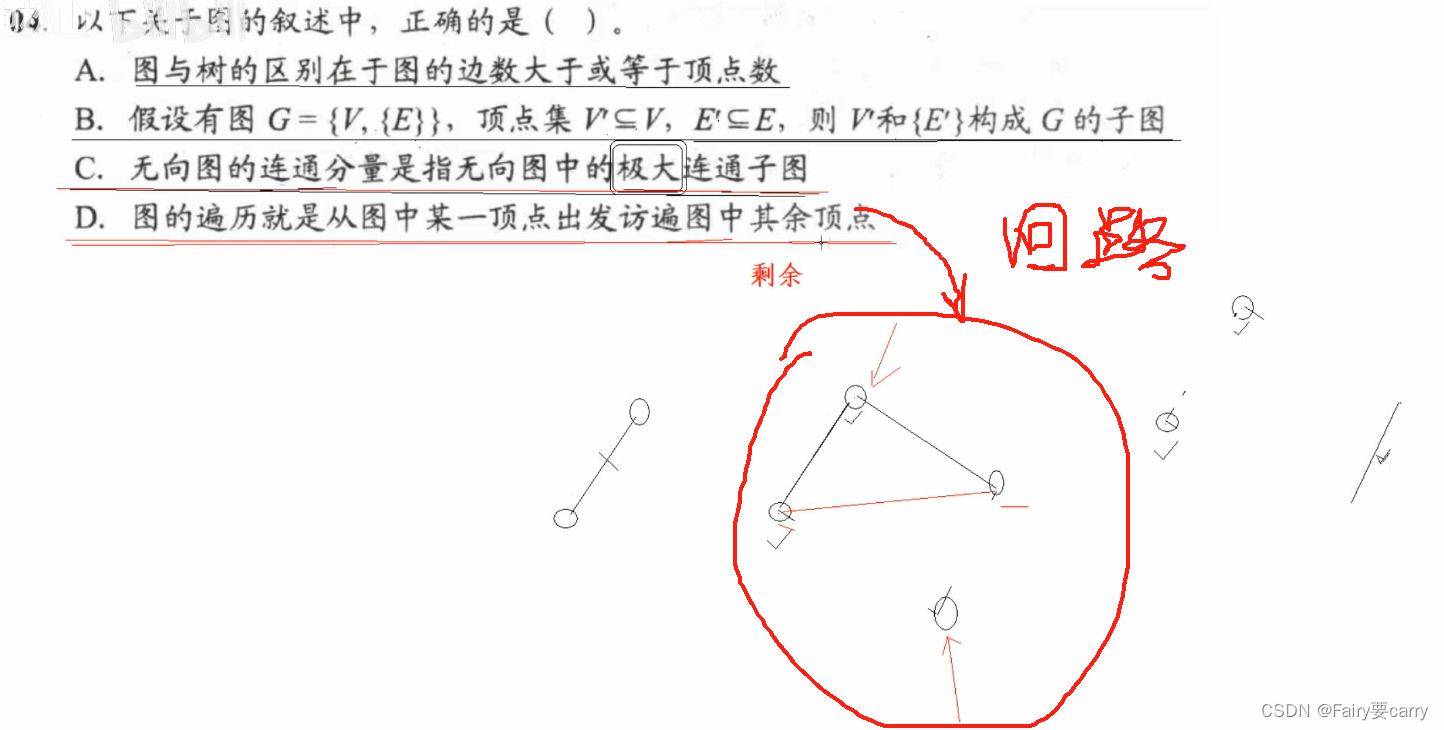
3.
强连通图的概念:
有方向,有边,但是强连通图不能保证任何顶点到其他所有顶点都有弧,可能只与其中之一之间有弧
图的入度和出度:
图的入度和出度不一定相等,入读可能为0
有向完全图:
有边且方向为双向,边数为n(n-1),故有向完全图一定为强连通图 (有边有方向)
有向图边集的子集和顶点的子集不一定能够构成子图:除非明确给出这个子集构成了个图
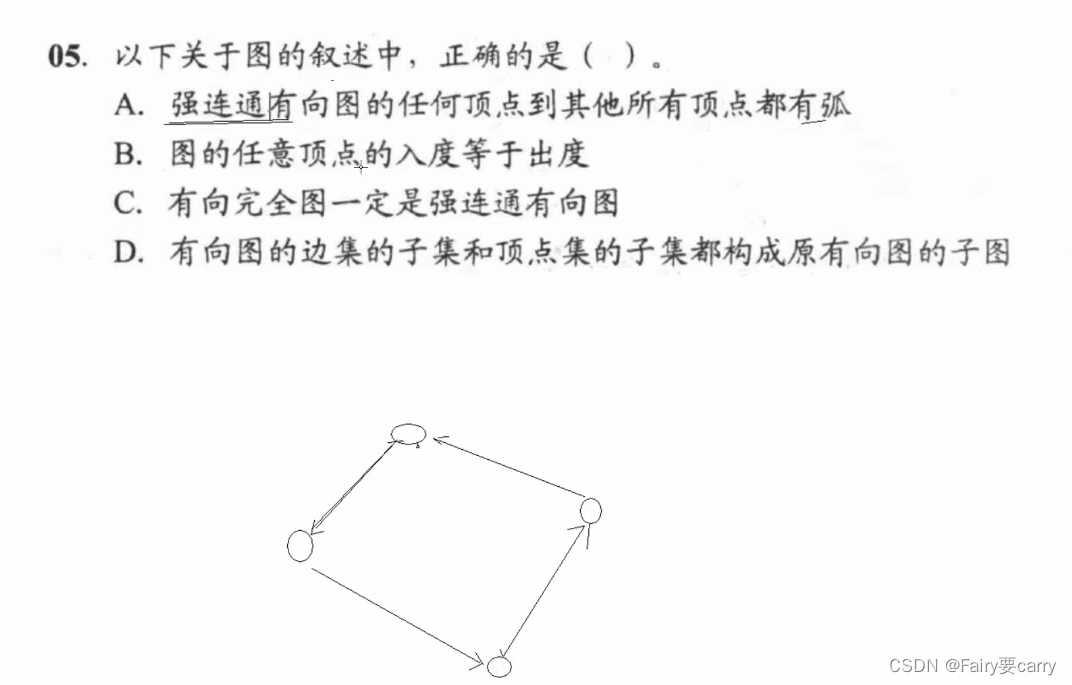
5.
注意非连通的情况

6.
对于强连通有向图,成一个环,三个节点三条边
你到我有路径,我到你有路径——>最少边数为n(环),至多边数为n(n-1);

7.
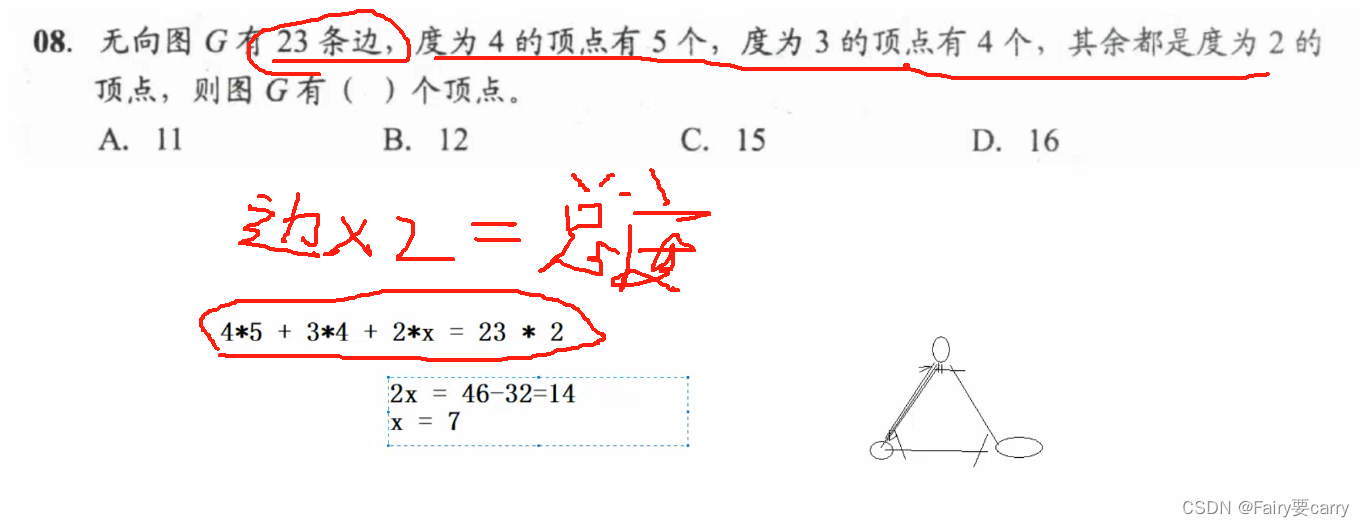
8.
n个顶点最多n-1条边,算入度出度,2*(n-1)

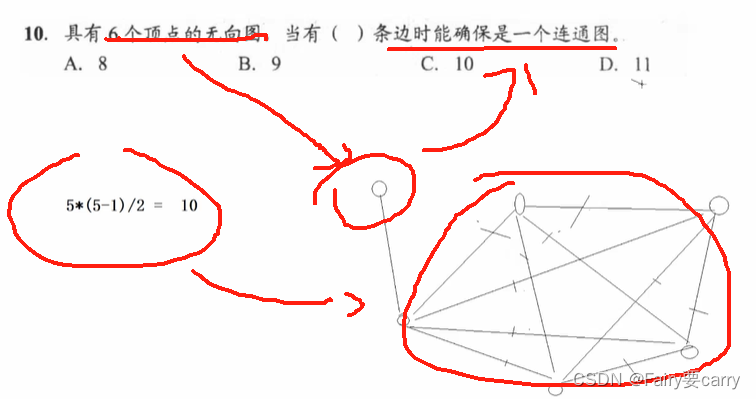
10.
在五个顶点的完全图基础之上再加一个顶点使其为连通图
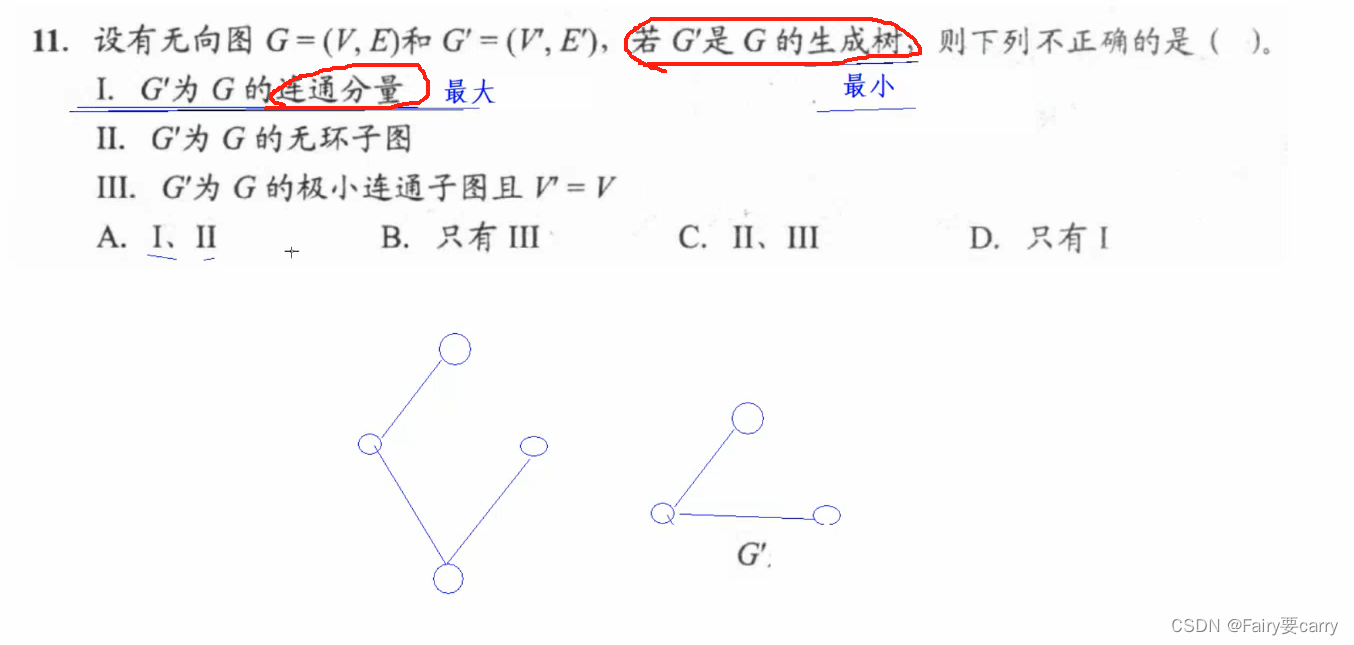
11.
可以知道的是树一定是一个连通图——>所以符合n个节点n-1条边
- 生成树指的是最小连通子树,而连通分量指的是极大连通子树
- 生成树确实是无环的
- 生成树与最下连通子树相关
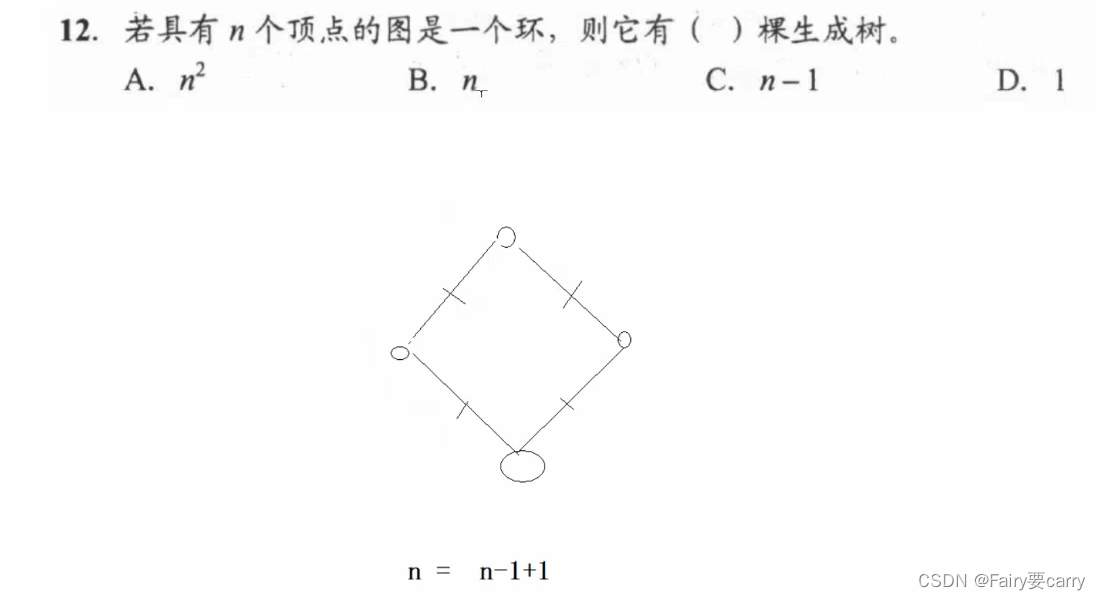
12.
n个顶点,成为一个环,有n个边,n个边有n颗生成树(也可以从度方面思考)
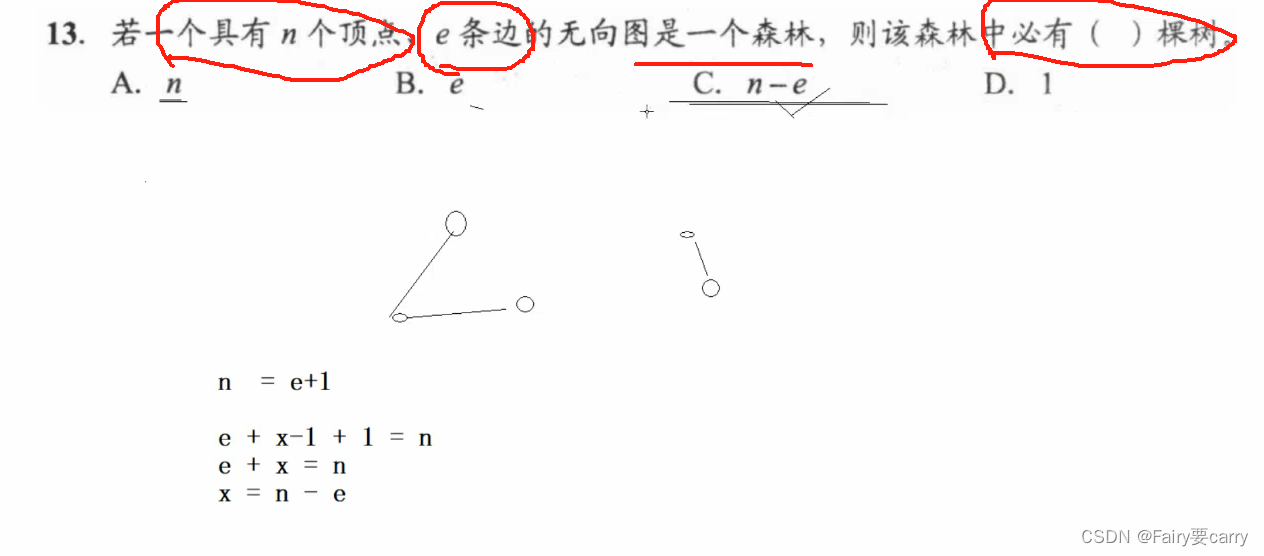
13.
设森林中有s棵树,再用n-1条边就能把所有的树连接成一棵树,此时,边数+1=顶点数,即e+(x-1)+1=n => x=n-e
14.
在有向图中,顶点的度为入度与出度之和。n个顶点的有向图中,任一顶点最多还可以与其他n—1个顶点有一对边相连。 2(n-1)*
15.
若图为环,则度最少为2
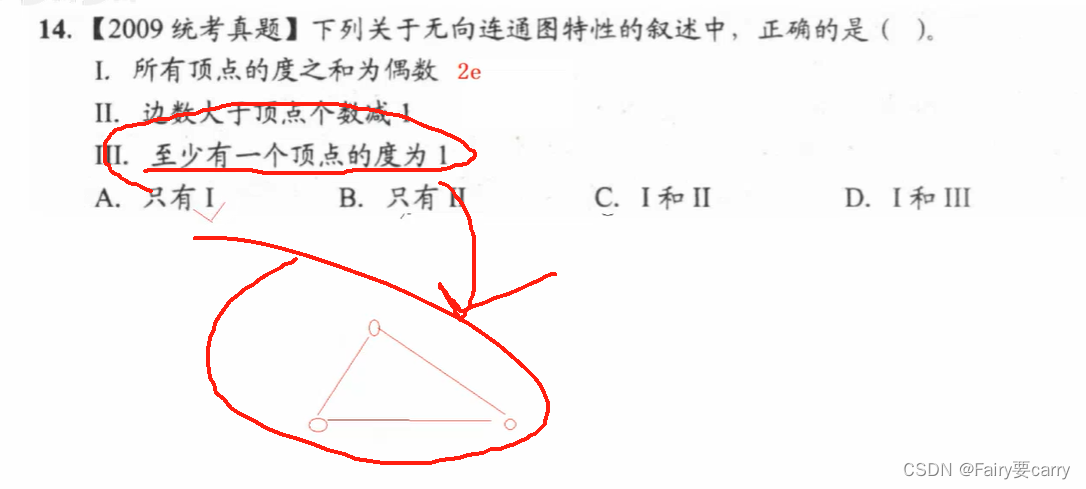
16.
与上述类似,一个无向图若要有七个节点,要保证它是连通的,说明六个节点的时候是完全图,所以边数为6*(5)/2,但因为要将其变为连通图,所以需要+1条边

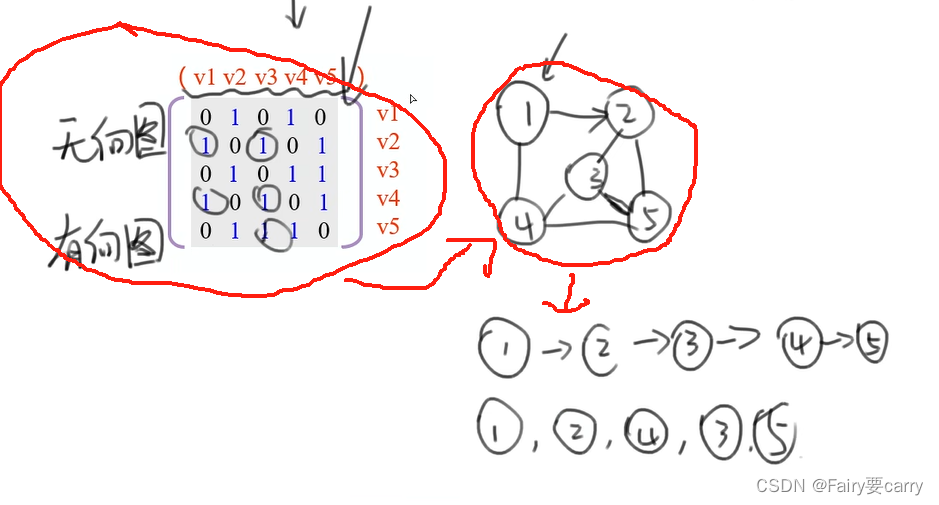
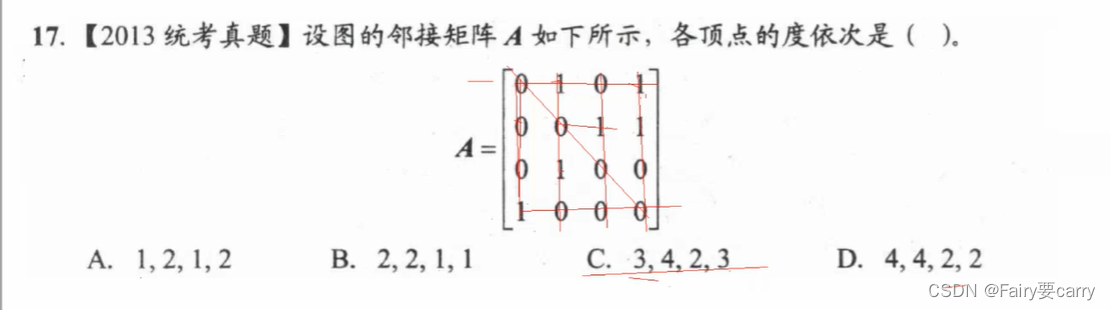
17.邻接矩阵:
非对称的邻接矩阵,说明为有向图,(因为无向图一定是对称的),各顶点的度依次是=入度+出度,为3423
如果是无向图,就要/2;
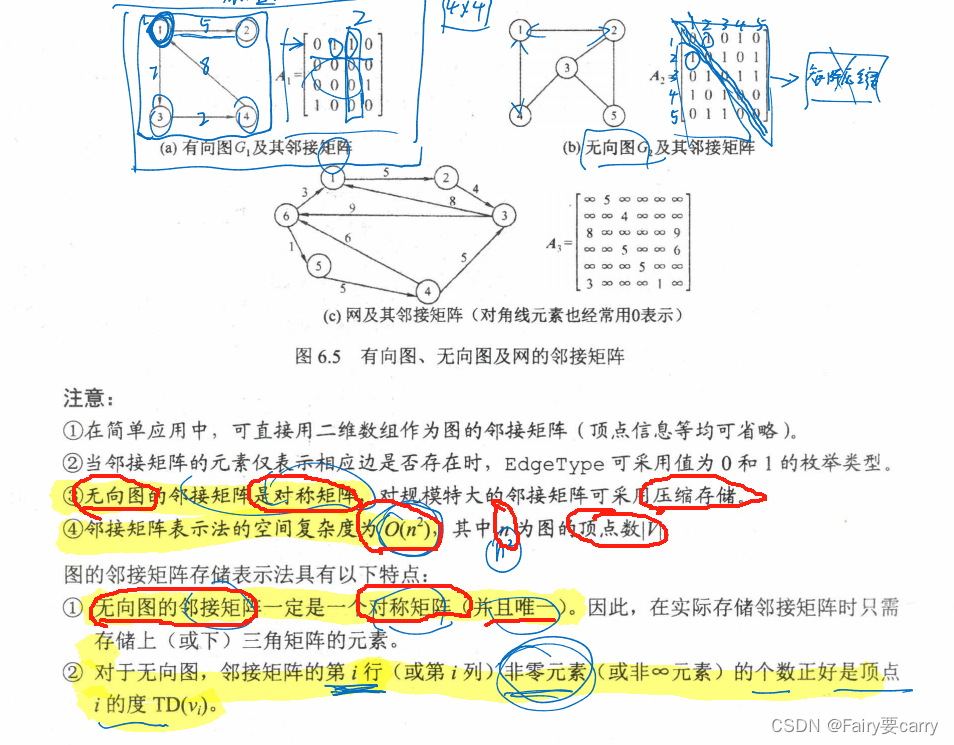
2.图的存储
邻接矩阵
无向图的邻接矩阵是唯一的;邻接表是唯一的
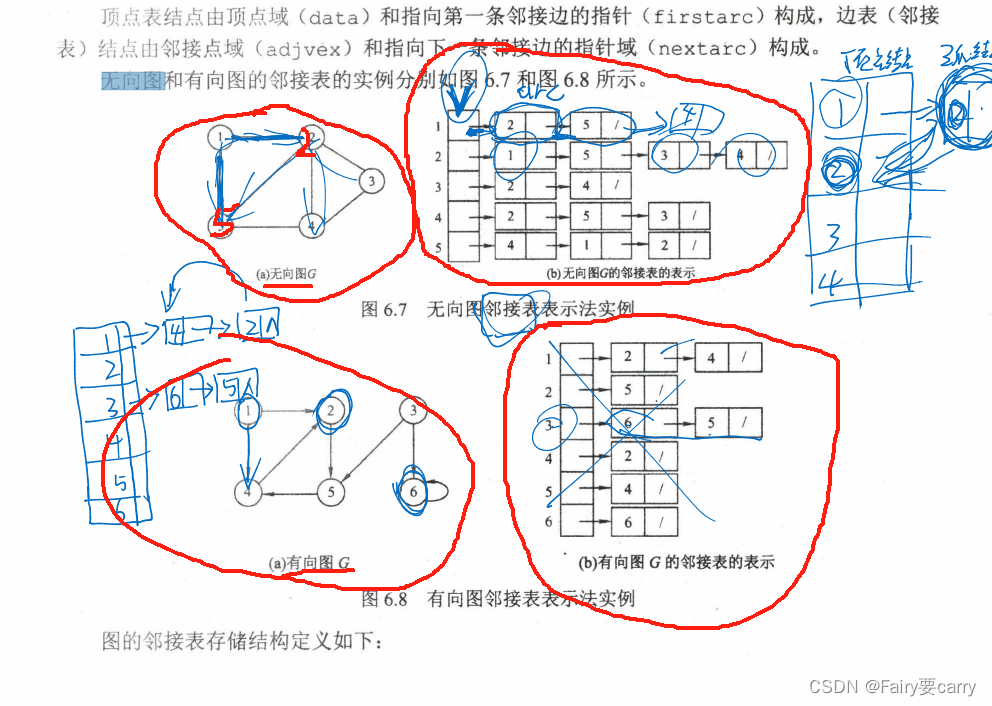
邻接表
**前提:**因为邻接矩阵较为稀疏,所以我们用邻接表法减少空间的消耗
-
有向图,无向图都能够存储
-
邻接表存储有向图时,顶点的出度个数为单链表中的节点个数
-
无向图中,邻接表不唯一,若无向图中有n个顶点、e条边,则其邻接表需要n个头结点和2e个表结点。适宜存储稀疏图。
-

-
无向图和有向图存储空间的比较
**无向图:**顶点数+2*边数;**有向图:**定点数+边数

图的遍历
深度优先DFS:
从上至下遍历,如果到顶了(已经走过的路就不走了),就返回上一步节点
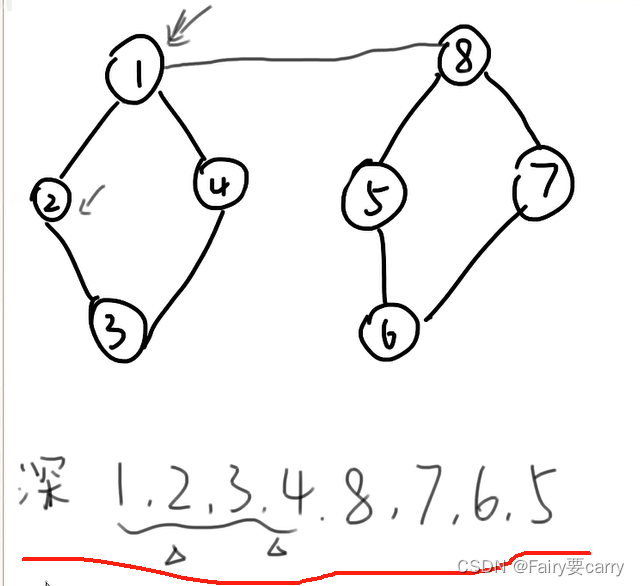
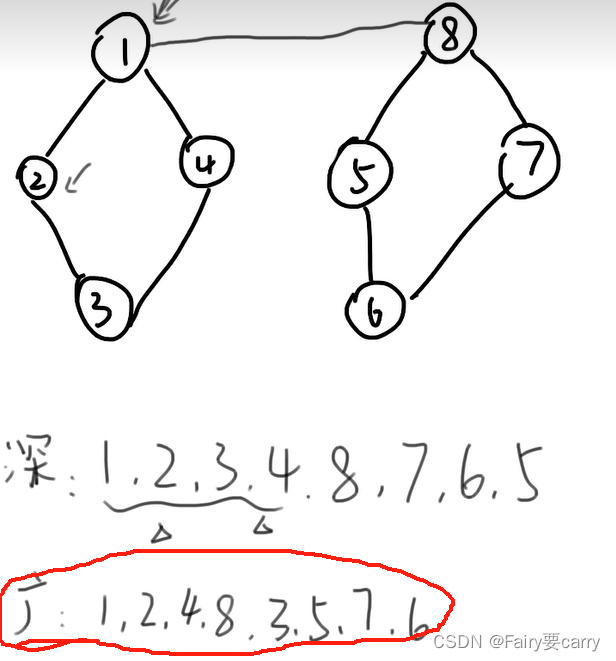
广度优先BFS:
从左到右一层一层遍历,放入(找当前节点距离为1的节点们,放入,然后继续遍历)
邻接矩阵的遍历:
注意遍历的唯一性