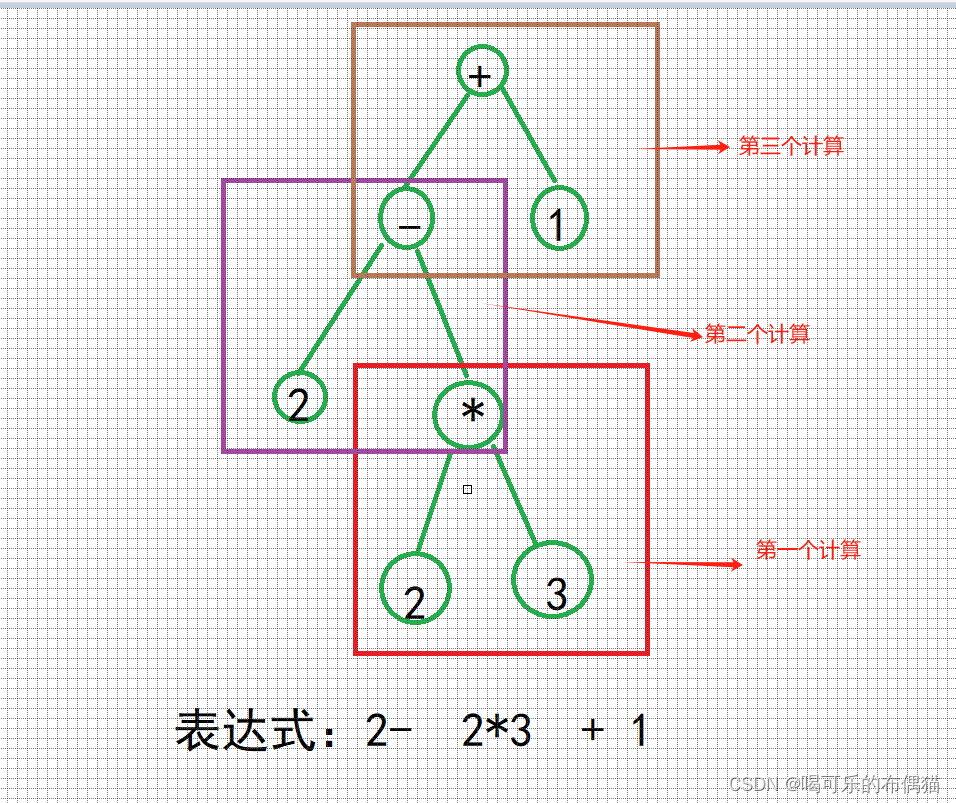
题目
您需要写一种数据结构,来维护一些数(都是绝对值以内的数)的集合,最开始时集合是空的。其中需要提供以下操作,操作次数q不超过
:
- 定义数x的排名为集合中小于x的数的个数+1。查询数x的排名。注意x不一定在集合里。
- 查询排名为x(x≥1) 的数。保证集合里至少有x个数。
- 求x的前驱(前驱定义为小于x,且最大的数)。若不存在则输出−2147483647。
- 求x的后继(后继定义为大于x,且最小的数)。若不存在则输出2147483647。
- 插入一个数x,本题的数据保证插入前x不在集合中。
保证执行1,3,4操作时,集合中有至少一个元素。
输入输出格式
输入格式
第一行是一个整数q,表示操作次数。
接下来q行,每行两个整数op,x,分别表示操作序号以及操作的参数x。
输出格式
输出有若干行。对于操作1,2,3,4,输出一个整数,表示该操作的结果。
输入输出样例
输入样例
7
5 1
5 3
5 5
1 3
2 2
3 3
4 3输出样例
2
3
1
5解析1
BST,二叉搜索树,又叫二叉排序树,是一棵空树或具有以下几种性质的树:
-
若左子树不空,则左子树上所有结点的值均小于它的根结点的值
-
若右子树不空,则右子树上所有结点的值均大于它的根结点的值
-
左、右子树也分别为二叉排序树
-
没有权值相等的结点。
第4条在数据中遇到多个相等的数我们可以多加一个计数器,就是当前这个值出现了几遍。
那么我们的每一个节点都包含以下几个信息:
-
当前节点的权值,也就是序列里的数
-
左孩子的下标和右孩子的下标,如果没有则为0
-
计数器,代表当前的值出现了几遍
-
子树大小和自己的大小的和
节点是这样的:
struct node{
int val,ls,rs,cnt,siz;
}tree[500010];
其中val是权值,ls /rs是左/右孩子的下标,cnt是当前的权值出现了几次,siz 是子树大小和自己的大小的和。
以下均以递归方式呈现。
插入:
x是当前节点的下标,v是要插入的值。要在树上插入一个v的值,就要找到一个合适v的位置,如果本身树的节点内有代表v的值的节点,就把该节点的计数器加1 ,否则一直向下寻找,直到找到叶子节点,这个时候就可以从这个叶子节点连出一个儿子,代表v的节点。具体向下寻找该走左儿子还是右儿子是根据二叉搜索树的性质来的。
void add(int x,int v)
{
tree[x].siz++;
//如果查到这个节点,说明这个节点的子树里面肯定是有v的,所以siz++
if(tree[x].val==v){
//如果恰好有重复的数,就把cnt++,退出即可,因为我们要满足第四条性质
tree[x].cnt++;
return ;
}
if(tree[x].val>v){//如果v<tree[x].val,说明v实在x的左子树里
if(tree[x].ls!=0)
add(tree[x].ls,v);//如果x有左子树,就去x的左子树
else{//如果不是,v就是x的左子树的权值
cont++;//cont是目前BST一共有几个节点
tree[cont].val=v;
tree[cont].siz=tree[cont].cnt=1;
tree[x].ls=cont;
}
}
else{//右子树同理
if(tree[x].rs!=0)
add(tree[x].rs,v);
else{
cont++;
tree[cont].val=v;
tree[cont].siz=tree[cont].cnt=1;
tree[x].rs=cont;
}
}
}
找前驱:
x是当前的节点的下标,val是要找前驱的值,ans是目前找到的比val小的数的最大值。
找前驱的方法也是不断的在树上向下爬找具体节点,具体爬的方法可以参考代码注释部分。
int queryfr(int x, int val, int ans) {
if (tree[x].val>=val)
{//如果当前值大于val,就说明查的数大了,所以要往左子树找
if (tree[x].ls==0)//如果没有左子树就直接返回找到的ans
return ans;
else//如果不是的话,去查左子树
return queryfr(tree[x].ls,val,ans);
}
else
{//如果当前值小于val,就说明我们找比val小的了
if (tree[x].rs==0)//如果没有右孩子,就返回tree[x].val,因为走到这一步时,我们后找到的一定比先找到的大(参考第二条性质)
return (tree[x].val<val) ? tree[x].val : ans
//如果有右孩子,,我们还要找这个节点的右子树,因为万一右子树有比当前节点还大并且小于要找的val的话,ans需要更新
if (tree[x].cnt!=0)//如果当前节数的个数不为0,ans就可以更新为tree[x].val
return queryfr(tree[x].rs,val,tree[x].val);
else//反之ans不需要更新
return queryfr(tree[x].rs,val,ans);
}
}
找后继
与找前驱同理,只不过反过来了,在这里我就不多赘述了。
int queryne(int x, int val, int ans) {
if (tree[x].val<=val)
{
if (tree[x].rs==0)
return ans;
else
return queryne(tree[x].rs,val,ans);
}
else
{
if (tree[x].ls==0)
return (tree[x].val>val)? tree[x].val : ans;
if (tree[x].cnt!=0)
return queryne(tree[x].ls,val,tree[x].val);
else
return queryne(tree[x].ls,val,ans);
}
}
按值找排名:
这里我们就要用到 siz了,排名就是比这个值要小的数的个数再+1,所以我们按值找排名,就可以看做找比这个值小的数的个数,最后加上1即可。
int queryval(int x,int val)
{
if(x==0) return 0;//没有排名
if(val==tree[x].val) return tree[tree[x].ls].siz;
//如果当前节点值=val,则我们加上现在比val小的数的个数,也就是它左子树的大小
if(val<tree[x].val) return queryval(tree[x].ls,val);
//如果当前节点值比val大了,我们就去它的左子树找val,因为左子树的节点值一定是小的
return queryval(tree[x].rs,val)+tree[tree[x].ls].siz+tree[x].cnt;
//如果当前节点值比val小了,我们就去它的右子树找val,同时加上左子树的大小和这个节点的值出现次数
//因为这个节点的值小于val,这个节点的左子树的各个节点的值一定也小于val
}
//注:这里最终返回的是排名-1,也就是比val小的数的个数,在输出的时候记得+1
按排名找值:
因为性质1和性质2,我们发现排名为n的数在BST上是第n靠左的数。或者说排名为n的数的节点在BST中,它的左子树的siz与它的各个祖先的左子树的siz相加恰好=n (这里相加是要减去重复部分)。
所以问题又转化成上一段或者说的后面的部分
rk是要找的排名
int queryrk(int x,int rk)
{
if(x==0) return INF;
if(tree[tree[x].ls].siz>=rk)//如果左子树大小>=rk了,就说明答案在左子树里
return queryrk(tree[x].ls,rk);//查左子树
if(tree[tree[x].ls].siz+tree[x].cnt>=rk)//如果左子树大小加上当前的数的多少恰好>=k,说明我们找到答案了
return tree[x].val;//直接返回权值
return queryrk(tree[x].rs,rk-tree[tree[x].ls].siz-tree[x].cnt);
//否则就查右子树,同时减去当前节点的次数与左子树的大小
}
删除:
具体就是利用二叉搜索树的性质在树上向下爬找到具体节点,把计数器-1。与上文同理。
完整代码
#include<iostream>
using namespace std;
const int INF=0x7fffffff;
int cont;
struct node{
int val,siz,cnt,ls,rs;
}tree[1000010];
void add(int x,int v){
tree[x].siz++;
if(tree[x].val==v){
tree[x].cnt++;
return;
}
if(tree[x].val>v){
if(tree[x].ls!=0){
add(tree[x].ls,v);
}
else{
cont++;
tree[cont].val=v;
tree[cont].siz=tree[cont].cnt=1;
tree[x].ls=cont;
}
}
else{
if(tree[x].rs!=0){
add(tree[x].rs,v);
}
else{
cont++;
tree[cont].val=v;
tree[cont].siz=tree[cont].cnt=1;
tree[x].rs=cont;
}
}
}
int queryfr(int x,int val,int ans){
if(tree[x].val>=val){
if(tree[x].ls==0){
return ans;
}
else{
return queryfr(tree[x].ls,val,ans);
}
}
else{
if(tree[x].rs==0){
return tree[x].val;
}
return queryfr(tree[x].rs,val,tree[x].val);
}
}
int queryne(int x,int val,int ans){
if(tree[x].val<=val){
if(tree[x].rs==0){
return ans;
}
else{
return queryne(tree[x].rs,val,ans);
}
}
else{
if(tree[x].ls==0){
return tree[x].val;
}
return queryne(tree[x].ls,val,tree[x].val);
}
}
int queryrk(int x,int rk){
if(x==0){
return INF;
}
if(tree[tree[x].ls].siz>=rk){
return queryrk(tree[x].ls,rk);
}
if(tree[tree[x].ls].siz+tree[x].cnt>=rk){
return tree[x].val;
}
return queryrk(tree[x].rs,rk-tree[tree[x].ls].siz-tree[x].cnt);
}
int queryval(int x,int val){
if(x==0){
return 0;
}
if(val==tree[x].val){
return tree[tree[x].ls].siz;
}
if(val<tree[x].val){
return queryval(tree[x].ls,val);
}
return queryval(tree[x].rs,val)+tree[tree[x].ls].siz+tree[x].cnt;
}
int main(){
int n,opt,xx;
cin>>n;
while(n--){
cin>>opt>>xx;
if(opt==1){
cout<<queryval(1,xx)+1<<endl;
}
else if(opt==2){
cout<<queryrk(1,xx)<<endl;
}
else if(opt==3){
cout<<queryfr(1,xx,-INF)<<endl;
}
else if(opt==4){
cout<<queryne(1,xx,INF)<<endl;
}
else{
if(cont==0){
cont++;
tree[cont].cnt=tree[cont].siz=1;
tree[cont].val=xx;
}
else{
add(1,xx);
}
}
}
return 0;
}解析2
使用multiset,它是C++STL里的一种容器。头文件 #include<set>
multiset性质:
- 里面的元素按顺序排列,默认升序。
- 不去重(这点和set是不同的)。
常用方法
multiset<int>q;
//定义一个multiset,尖括号里写类型
//如果是自定义类型,需要重载小于号
q.insert(x);
//插入一个数 x
q.clear();
//清空
q.erase(x);
//删除容器中的所有值为 x 的数
q.erase(it);
//删除容器中迭代器it指向的元素
q.empty();
//返回bool值,如果容器为空返回true,否则返回false
q.size()
//返回元素个数
q.begin();
//返回首个元素的迭代器
q.end();
//返回最后一个元素的下一个位置的迭代器
q.count(x);
//返回容器中 x 的个数
q.find(x);
//返回容器中第一个x的位置(迭代器),如果没有就返回q.end()
q.lower_bound(x);
//返回容器中第一个大于等于x的数的迭代器
q.upper_bound(x);
//返回容器中第一个大于x的数的迭代器
分析题目
1. 查询 x 数的排名
用lower_bound方法,找到第一个x的位置。
然后从begin开始往后遍历容器,只要达到这个位置,就输出当前下标即可。
2.查询排名为 x 的数
遍历容器,只要当前排名到达x,就输出当前值。(因为multiset容器无法进行随机访问)
3.求 x 的前驱(前驱定义为小于 x,且最大的数)
前驱,也就是x的前一个。用lower_bound方法找到第一个x的位置,然后输出上一个就OK了。
4.求 x 的后继(后继定义为大于 x,且最小的数)
后继,也就是第一个大于x的数。用upper_bound方法,直接找到这个值。
5.插入一个数 x
直接用insert方法插入即可。
完整代码
#include<iostream>
#include<cmath>
#include<algorithm>
#include<set>
using namespace std;
multiset<int>q;
int n,t,x,order;
int main()
{
q.insert(-0x7fffffff);
q.insert(0x7fffffff);
//提前放入这两个数,避免错误
cin>>n;
while(n--)
{
cin>>t>>x;
if(t==1)
{
multiset<int>::iterator it=q.lower_bound(x);
order=0;
for(multiset<int>::iterator i=q.begin();i!=it;i++,order++);
cout<<order<<endl;
}
else if(t==2)
{
order=-1;
for(multiset<int>::iterator it=q.begin();it!=q.end();it++)
{
order++;
if(order==x)
cout<<*it<<endl;
}
}
else if(t==3)
{
multiset<int>::iterator it=q.lower_bound(x);
cout<<*--it<<endl;
}
else if(t==4)
{
cout<<*q.upper_bound(x)<<endl;
}
else
{
q.insert(x);
}
}
return 0;
}