题目描述:
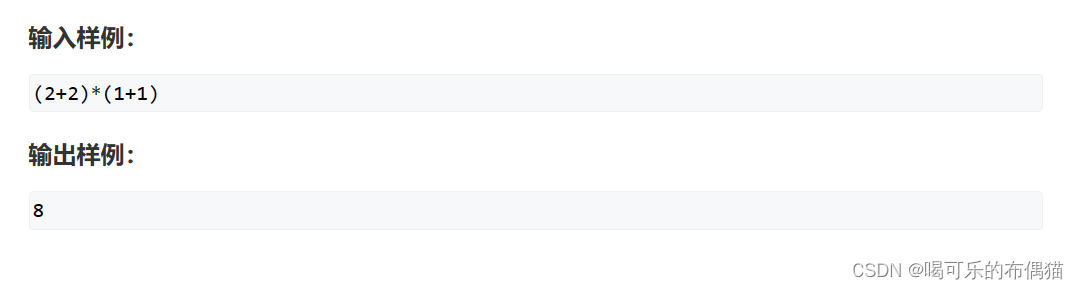
分析:
此题是acwing的一个模板例题,利用中缀遍历解决,即可。
思路:
首先我们先了解一下什么是树的中序遍历?
中序遍历是 二叉树遍历 的一种,也叫做 中根遍历 、中序周游。 在二叉树中,中序遍历首先遍历左子树,然后访问根结点,最后遍历右子树。
如果有不了解中序遍历的小伙伴可以看一下这篇大佬文章:看懂二叉树的三种遍历_二叉树遍历的三种方法-CSDN博客
再来看一下这个题
“假设”我们有一颗二叉树,它的叶子结点是数字,其它结点(根节点)是运算符。
这颗二叉树自根节点至叶子结点运算符的优先级逐级递增,也即根节点的优先级最低。
所以我们只需要将左右子树结果计算出来后,再根据根节点计算最终结点即可。
人为去建立一颗这样的树很麻烦,我们可以用栈模拟这样的一个过程。
我们发现,想要计算某个结点的运算符,必要条件是左右子树都已经计算完。
比如:(1+1)*(2+2),显然由于括号的存在,此处‘’的优先级要低于此处的‘+’,我们要计算‘’需要先计算两边的‘+’。
如图:
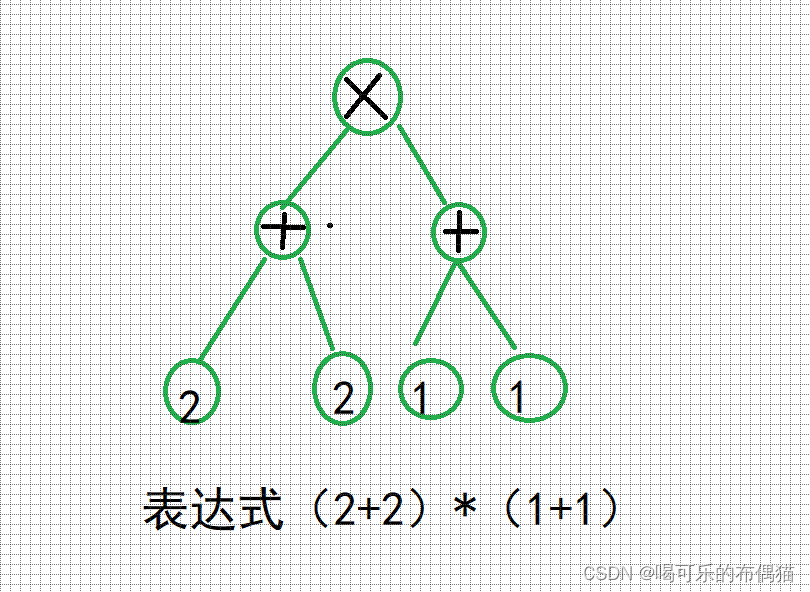
我们应该如何判断一个结点的左右子树已经遍历完?
由于我们”假设“,存在的这棵树根节点的运算符优先级最低,所以这颗树从底部往上走,运算符的优先级就越低,所以当我们遇到当前运算符的优先级小于等于上一个运算符时,该结点的左右子树已经计算完。该结点的左右子树已经计算完。也就是这句话:while(!op.empty()&&pr[x]<=pr[op.top()]) eval();
在入栈前将栈内优先级更高的运算符计算完再入栈。另外因为括号无视优先级,需要优先计算括号内的数,那么我们在遇到‘)’时可以直接将栈内的数从后向前计算出来
(在入栈时已经保证了优先级自后向前升高),直到遇到‘(’停止。
这样,这棵树就完美的用栈模拟出来了。解释如下图
如图:

以上话术来源于acwing的评论区一位大佬给出,我总结一下。
实现:
(1)双栈,一个操作数栈,一个运算符栈;
(2)运算符优先级,栈顶运算符,和,即将入栈的运算符的优先级比较:
如果栈顶的运算符优先级低,新运算符直接入栈
如果栈顶的运算符优先级高,先出栈计算,新运算符再入栈


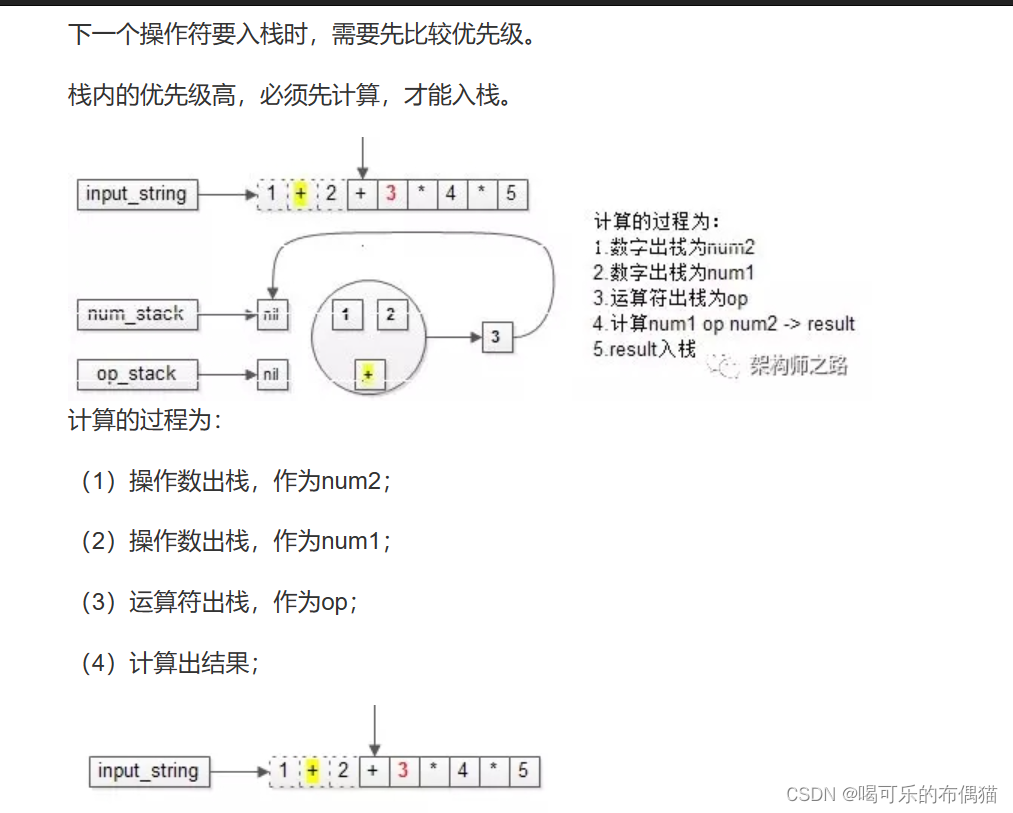

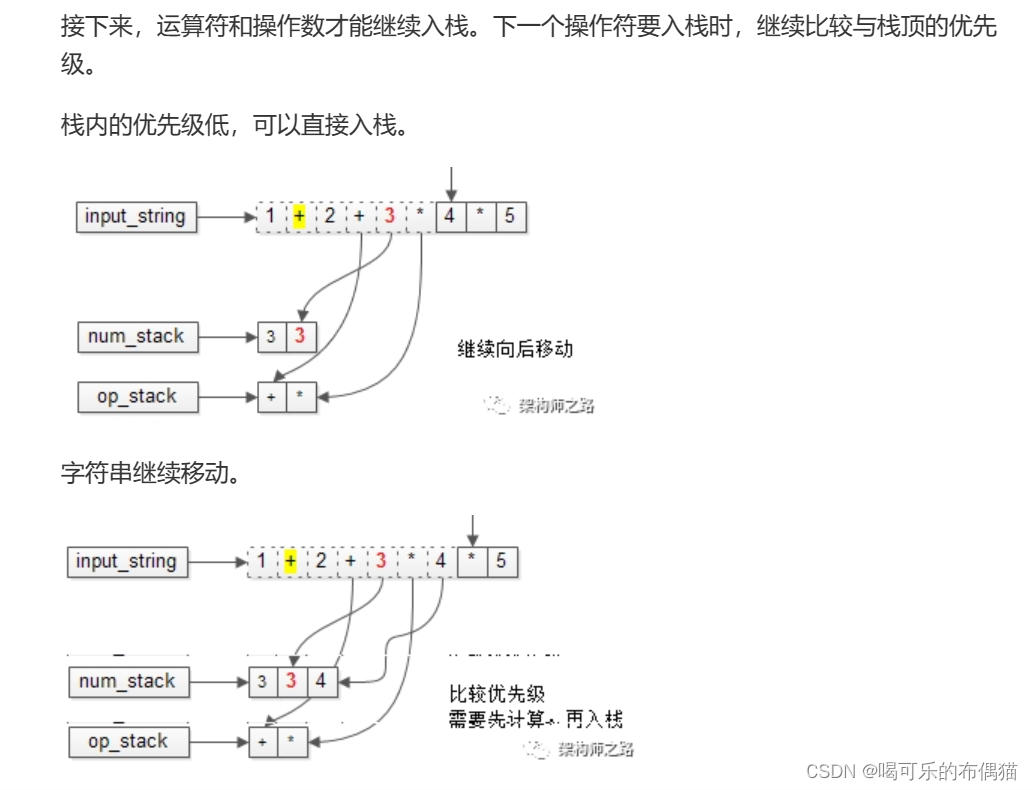
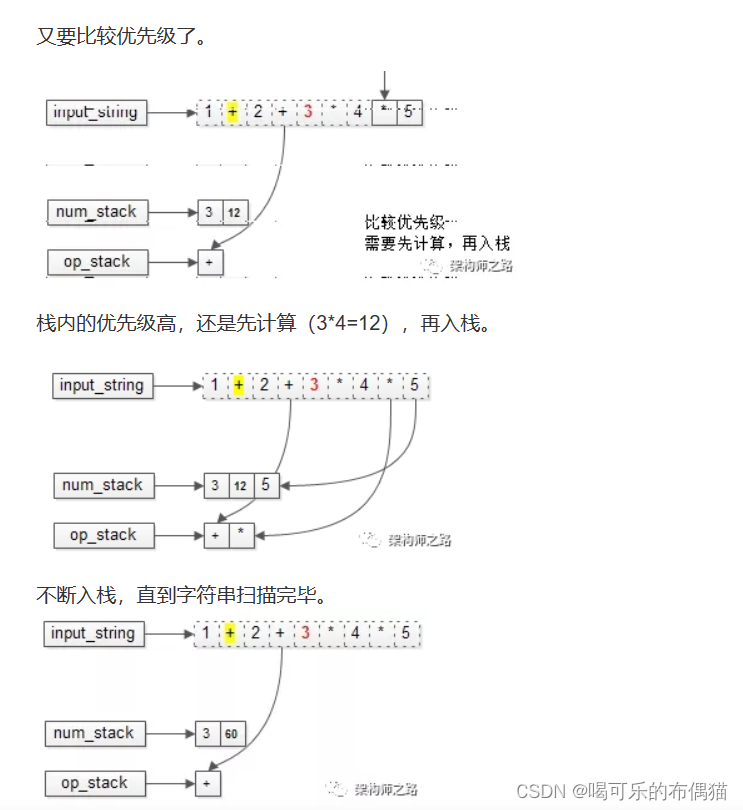
出栈最终结果是63
以上面的图片来源于acwing的题解 ,思路很清晰~
AcWing 3302. 表达式求值:多图讲解运算符优先级+详细代码注释 - AcWing
例题:
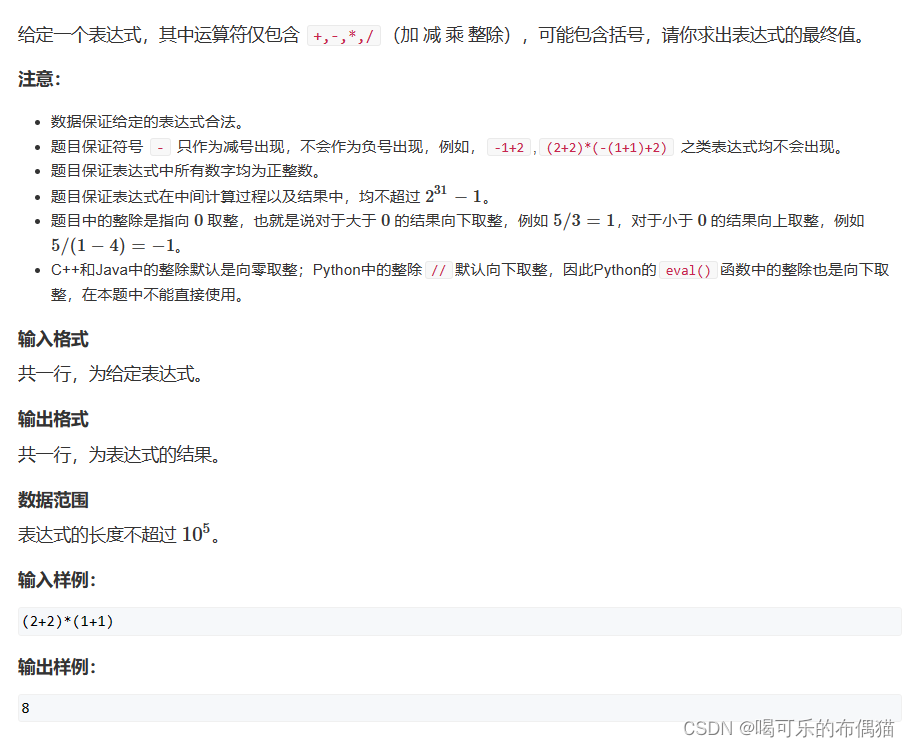
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<stack>
#include<unordered_map>
using namespace std;
stack<int> num;
stack<char> op;
//计算加减乘除函数
void eval()
{
//数第二个数(但是实则是栈顶元素),方便后面做除法和减法
//因为除法和减法,两个数不能换位置
auto num2 = num.top();
num.pop(); //出栈
//数第一个数(但是实则是栈顶元素的下面一个)
auto num1 = num.top();
num.pop(); //出栈
//运算符号
auto c = op.top();
op.pop();
int x = 0;
if(c == '+') x = num1 + num2;
else if(c == '-') x = num1 - num2;
else if(c == '*')x = num1 * num2;
else x = num1 / num2;
num.push(x); //计算结果入栈。
}
int main()
{
//符号的等级
unordered_map<char,int> pr{{'+',1},{'-',1},{'*',2},{'/',2}};
string str;
cin >> str;
for(int i=0;i<str.size();i++)
{
auto c = str[i];
//判断一下c是否为数字(isdigit函数)
if(isdigit(c))
{
int x = 0,j = i;
//双指针算法
while(j < str.size() && isdigit(str[j]))
{
//算下一数字位数,例如:1111*22+1
x = x * 10 + (str[j++] - '0');
}
i = j - 1;
num.push(x);
}
else if(c == '(') //判断是否是左括号
{
op.push(c); //左括号直接入栈
}
else if(c == ')')
{
while(op.size() && op.top()!='(') eval();
op.pop();
}
else
{
//如果栈顶运算符优先级较高,先操作栈顶元素再入栈
while(op.size() && pr[op.top()] >= pr[c]) eval();
//否则直接入栈
op.push(c);
}
}
//把没有操作完的运算符操作一遍
while(op.size()) eval();
//栈顶元素为最终答案
cout << num.top() << endl;
return 0;
}while (op.size() && pr[op.top()] >= pr[c]) eval(); 这里是while而不是if的原因
假如表达式为2-2*3+1,直到2-2*3都没有运算,遇到+的时候,先运算了2*3,还剩2-6
如果是if的话,就会把+和1入栈,栈里成了2-6+1,会先运算栈顶的6+1,再运算2-7,最终运算错误。
而如果是while,则会先运算2-6,再运算-4+1,运算正确。思想就是当前树的子树都运算完了,再运算当前树的根节点
如下图:
如图:
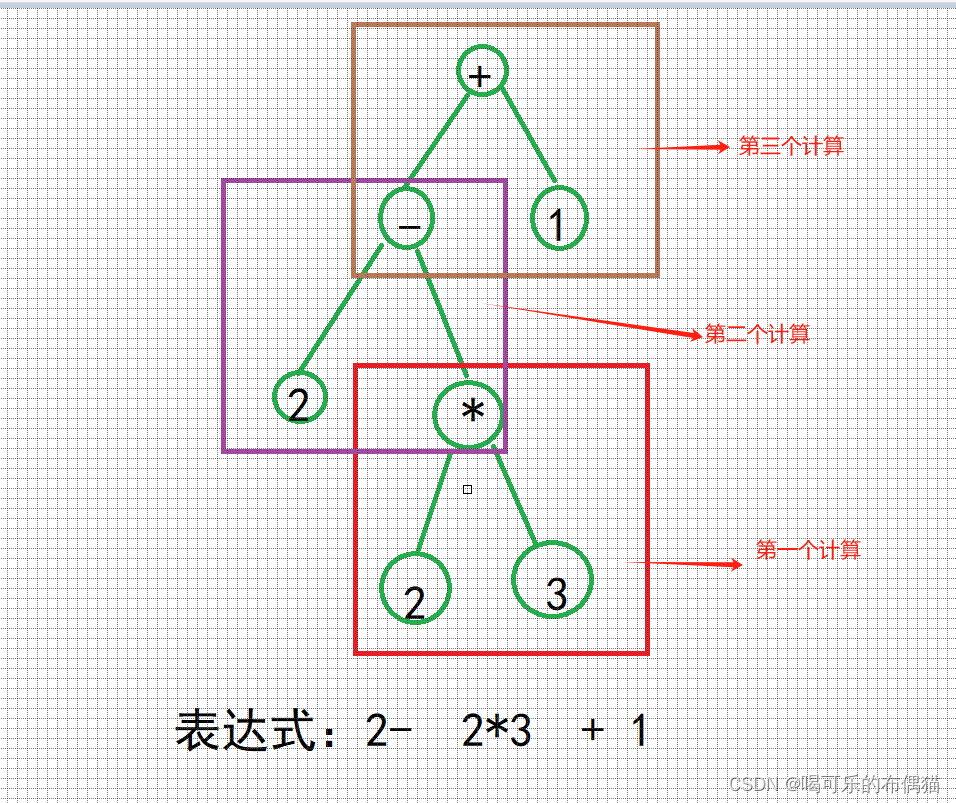
总结:
上述大部分都来源于acwing的评论区和题解,图片有的为本人所画,如有错误欢迎指出。
我的理解就是,本题采用去用一棵树的中序遍历去模拟此题,然后去用双栈实现。