运筹学后半段
第五章 动态规划
最优化原理,可以归结为一个递推公式
现实应用:比如最优路径、资源分配、生产计划和库存等
5.1 动态规划的最优化原理及其算法
5.1.1 求解多阶段决策过程的方法
例如:最短路径问题
求A到B的最短路径:
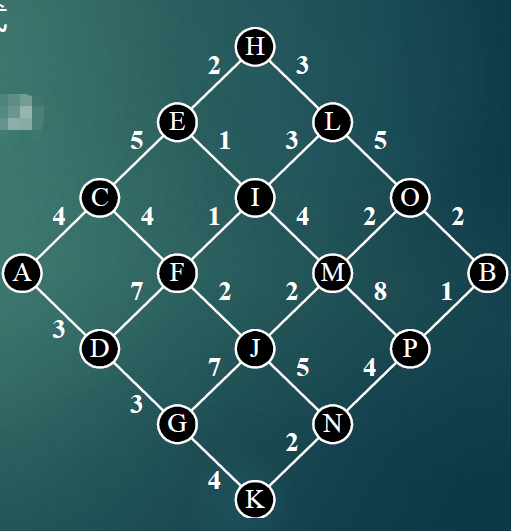
大体思路:递归
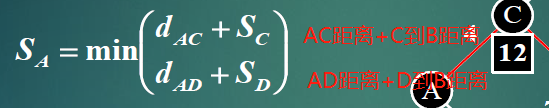
5.1.2 动态规划的基本概念及递推公式
- 基本概念


- 最优化原理和动态规划递推关系
最优化原理:最优策略的子策略也是最优的
递推关系:
路径加和累计
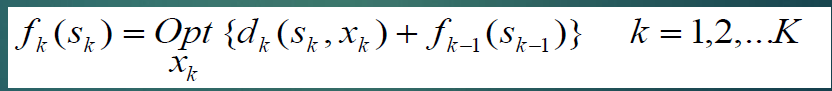
连乘累计
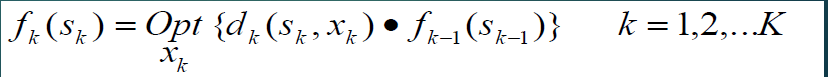
- 动态规划的步骤

5.2 动态规划模型举例
5.2.1 资源分配问题(重点)
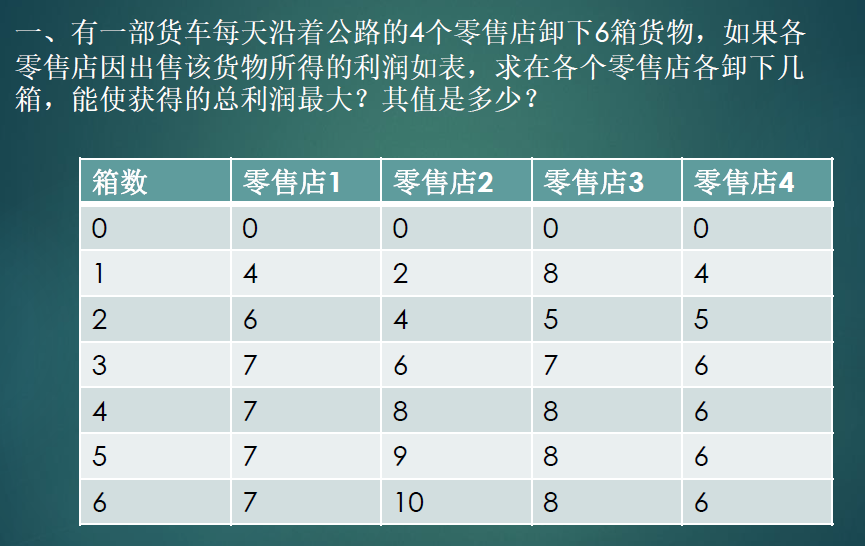
解

逆向开始书写:
X*:最终实际应该给多少
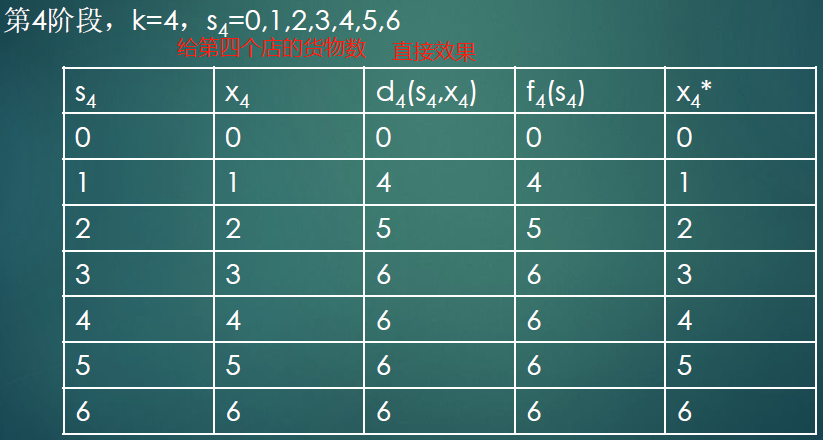 $$ f_3=Max(d_3+f_4) $$
$$ f_3=Max(d_3+f_4) $$
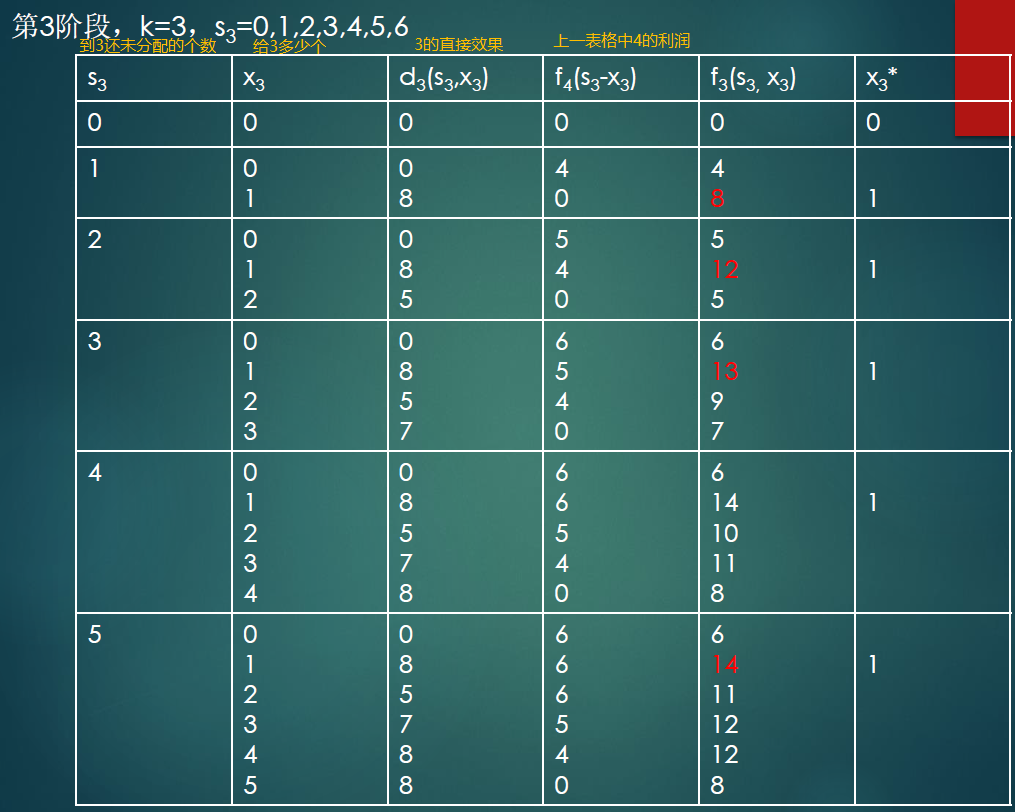

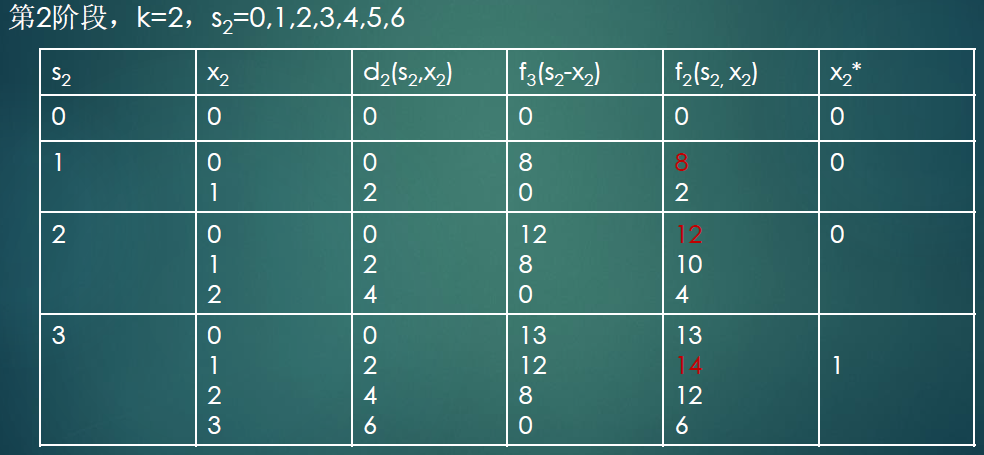
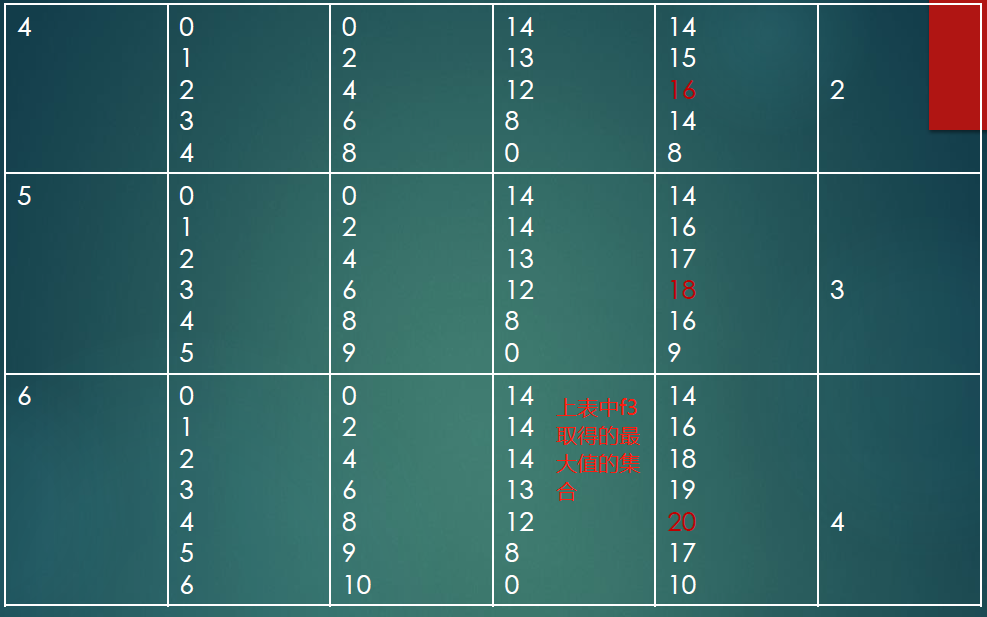
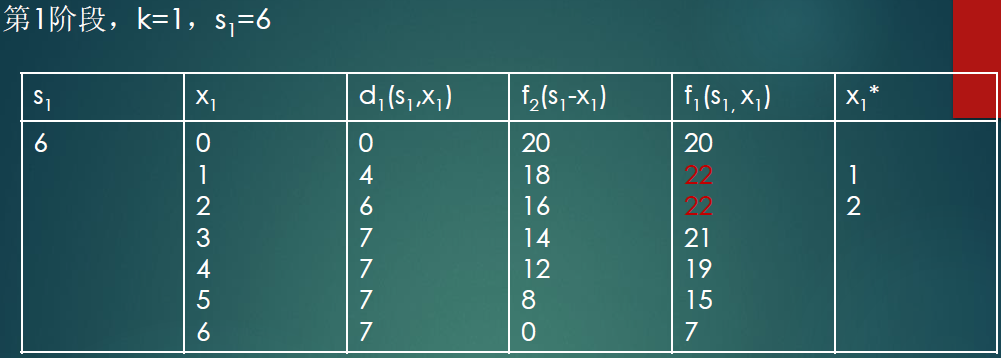
结论

第六章 图与网络分析
定义:
1)图与网络
简单图:既没有自环也没有平行边的图
**‘有向图’😗*每条边都有方向
**‘完全图’😗*任意两个点都有边
n个顶点有 Cn 2个边
**‘网’😗*边或者弧带权值的图
**‘顶点的度(degree)’😗*与该顶点相关联的边的数目
度为0的点:孤立点
度为1的点:悬挂点
链(link):连续的边构成的顶点序列
圈(loop):第一个顶点和最后一个顶点相同的链
‘路径’:连续的边构成的顶点序列,且不出现重复
**‘路径长度’😗*路径的权值之和
**‘回路(circuit)’😗*第一个顶点和最后一个顶点相同的路径
走过图中所有边且每条边仅走一次的闭行走称为欧拉回路
**‘简单路径’😗*除了路径起点和终点相同,其余顶点都不同
**‘连通图’😗*对任意两个顶点都有路径
‘联通分量(极大连通子图)’:再加入一个顶点子图不再连通
平面图(planar graph):在平面上可以画出该图而没有任何边相交
2)最小生成树
图的生成树:(重点)
生成树是图的所有顶点连接在一起,但不形成回路
‘深度优先生成树’:通过深度优先搜索进行遍历的生成树
‘广度优先生成树’:通过广度优先搜索进行遍历的生成树
最小生成树 (各边权值和最小)
‘MST性质(贪心算法)’:'U集合’是已经经过的顶点,在’U’和’U-V’选取权值最小的边,这条边一定在生成树上
Prim算法(选顶点)
(从a结点开始遍历,如果同时出现多个可以选择的结点时,优先把序号较小的结点加入生成树)

Kruskal(选择边)
(如果同时出现多个可以选择的边时,以边中序号较小的结点为第一优先,序号较大的结点为第二优先,按照升序顺序选择。假设边(a,d),(a,e),(b,c)有相同权重,选择优先顺序从大到小为(a,d),(a,e),(b,c))

最短路径(重点)
不同于最小生成树,不用包含全部的顶点
Dijkstra算法(解决到达一个点的最短路径)
步骤:
1.‘初始化’:先找出原点v0到所有顶点的最短路径(v0,vk)
S={v0},T={其余顶点},D[i]存放距离值
2.‘选择’:从这些路径中学出一条长度最短的路径(v0,u)
3.‘更新’:若存在(u,vk)且路径(v0,u,vk)<(v0,vk) 用其代替
4.(v0,u,vk)作为新的顶点集合,重复操作
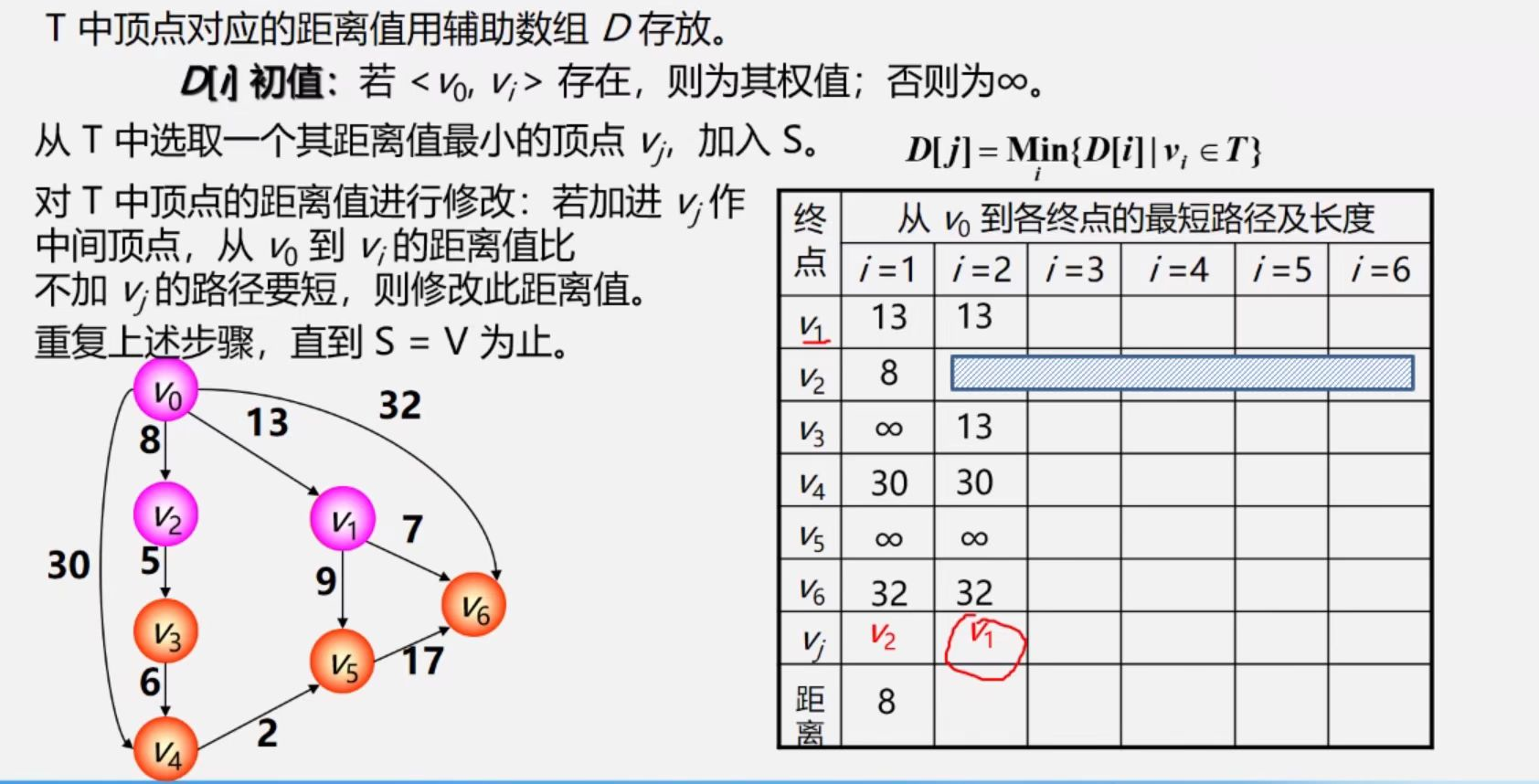
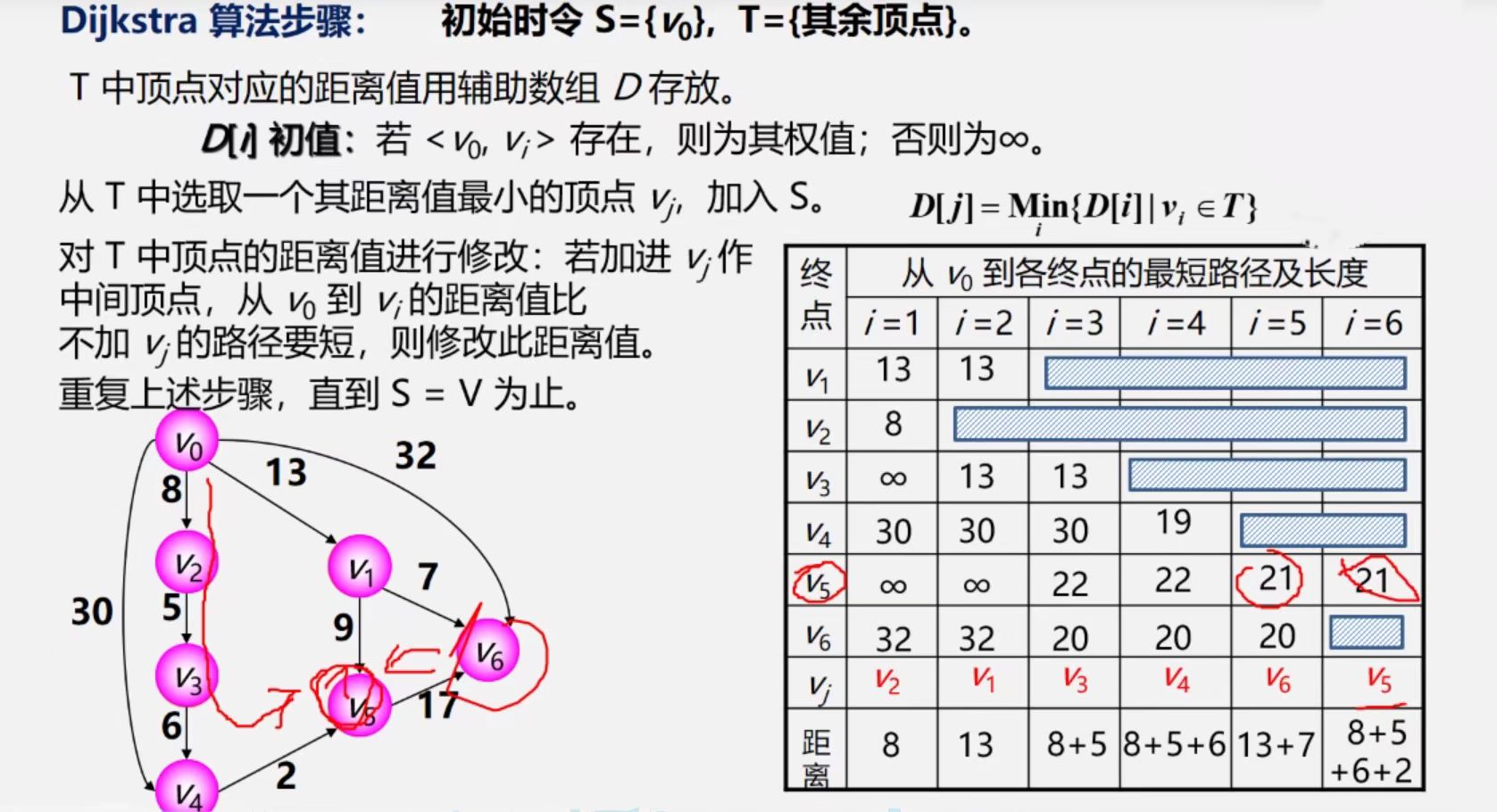
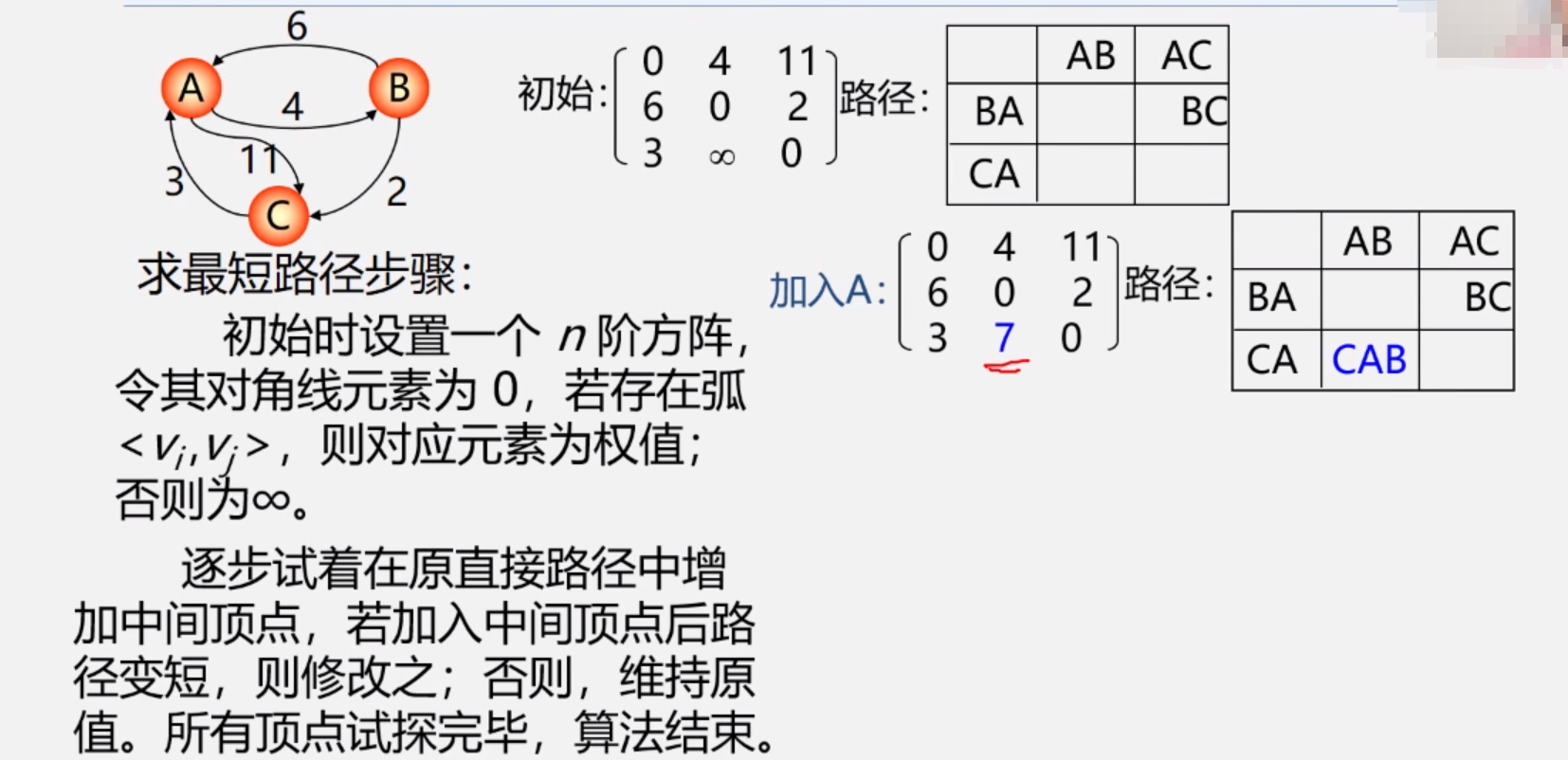
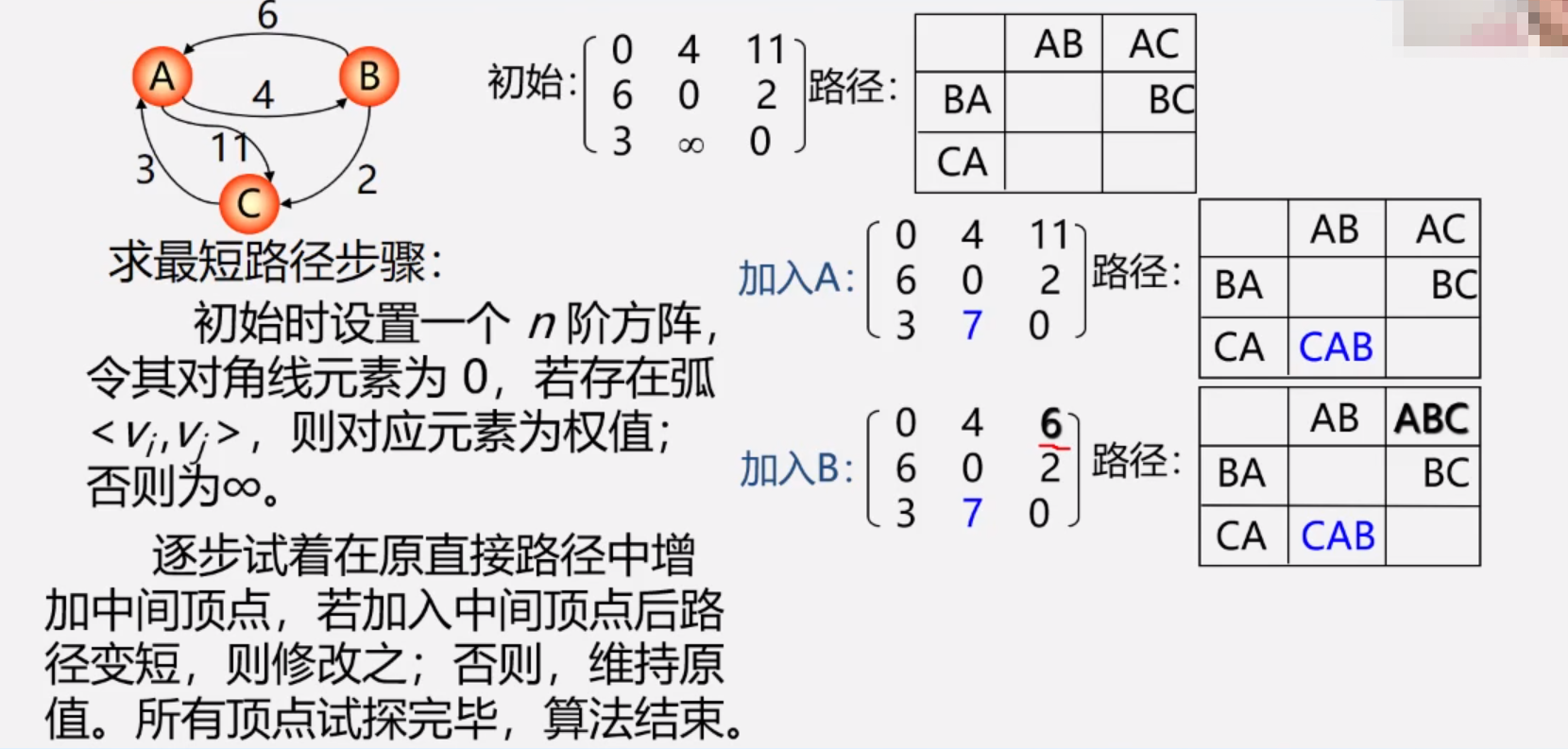
Floyd算法(解决所有顶点的最短路径)
步骤:
n阶矩阵,对角线元素为0,矩阵存的为对应权值
依次加入中间顶点,如果变短则修改,直到所有点增加完毕
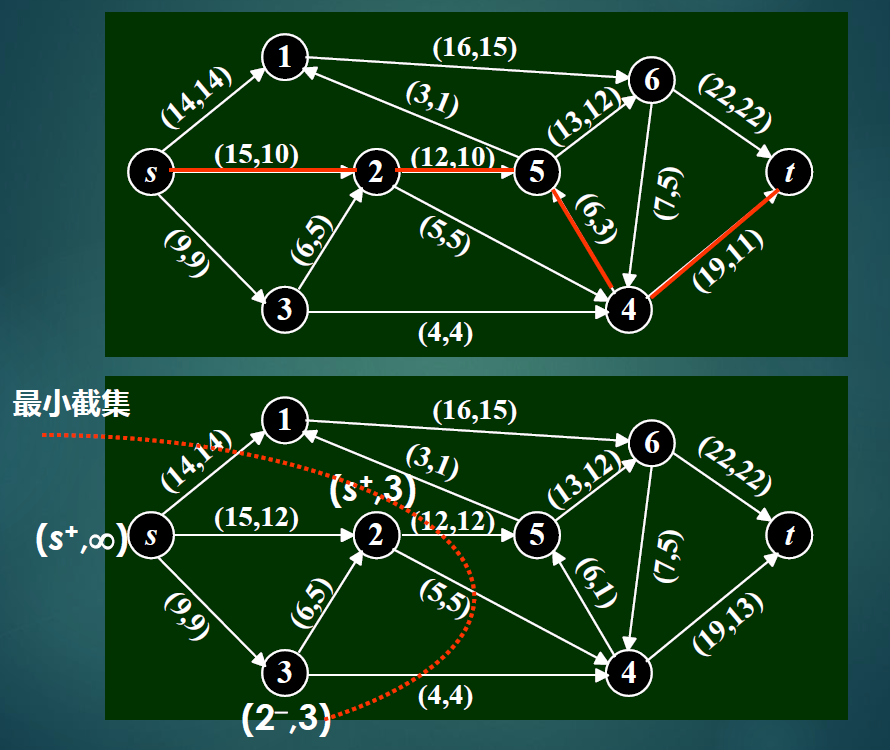
3)网络的最大流和最小截集(重点)

- 满足上述条件的称为可行流,存在最大可行流
- 当支路上fij = cij ,称为饱和弧
截集与截集容量
s:开始点,t:结束点
定义:
- 截集:把网络分割为两个成分的弧的最小集合,其中一个成分包含s 点,另一个包含t 点。
- 最小截集:所有点到外部都是满载的点
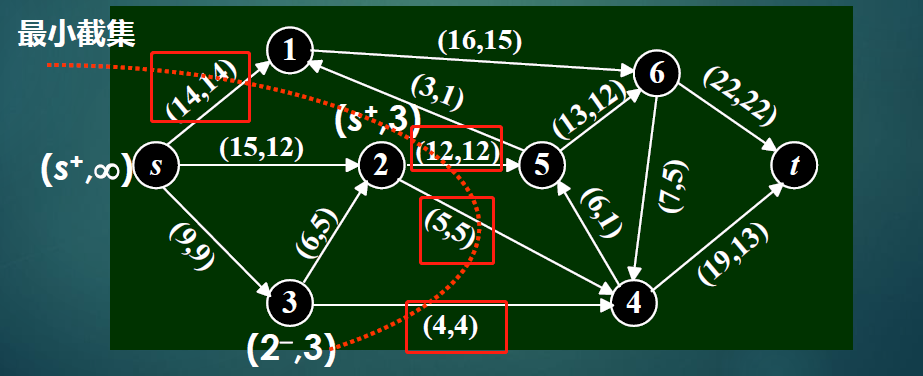
福特-富克森定理:网络的最大流等于最小截集容量
确定网络最大流的标号法
-
饱和弧:fij = cij 的弧
-
非饱和弧:fij < cij 的弧
-
零流弧:fij = 0的弧
-
非零流弧:fij >0 的弧
规定链μ:的方向是从始点s到终点t
-
正向弧:
-
第一类是弧的方向与链μ的方向一致,称为前向弧(正向弧),前向弧的全体集合记为μ+;
-
反向弧:第二类是弧的方向与链μ的方向相反,称为后向弧(反向弧),后向弧的全体集合记为μ-
-
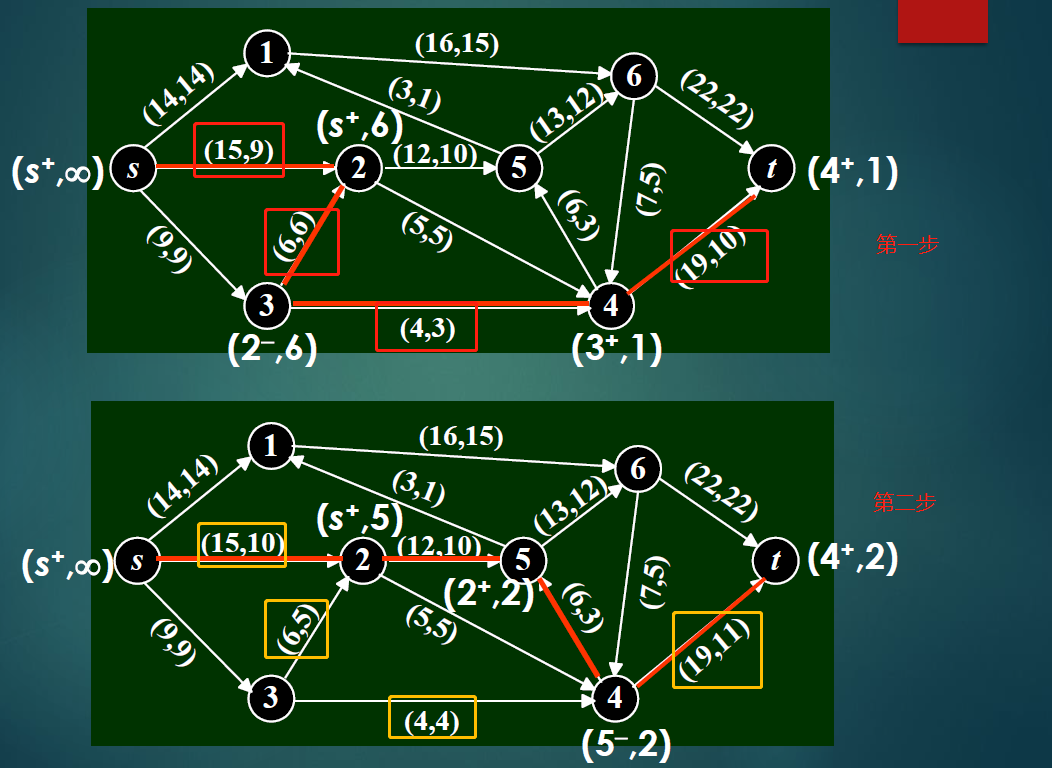
增广链:
理解:从原点可以增加多少流量到该结点
当μ满足下述条件:
即μ上的前向弧(正向弧)为非饱和弧,后向弧(反向弧)为非零流弧。

第一步

第二步

例:
如Dijkstra一样,每次合并后所有结点视为一个整体(找的增广链先后顺序无所谓)
第七章 随机服务理论概述
7.1 随机服务系统
定义介绍:
- 系统的输入输出是随机变量,可以称之为排队论和拥塞理论
相关特性

7.1.1 服务机构的组织方式与服务方式
- 单台制和多台制
- 并联服务
- 串联服务
- 串并联服务、网络服务
7.1.2 输入过程与服务时间
- 顾客单个到达或成批到达
- 顾客到达时间间隔的分布和服务时间的分布
- 顾客源是有限的还是无限的
7.1.3 服务规则
- 损失制
- 等待制:先到先服务 ( FIFO),后到先服务,随机服务,优先权服务
上述两个为重点学习内容
- 混合制
- 逐个到达,成批服务;成批到达,逐个服务
7.2 随机服务过程
- 单台服务系统、等待制、先到先服务
- 顾客在系统中的总时长:逗留时间=等待时长+服务时长
- 等待时长与顾客到达率和服务时长有关
例:
间隔到达时间:τ
等待时长:w
服务时长:h
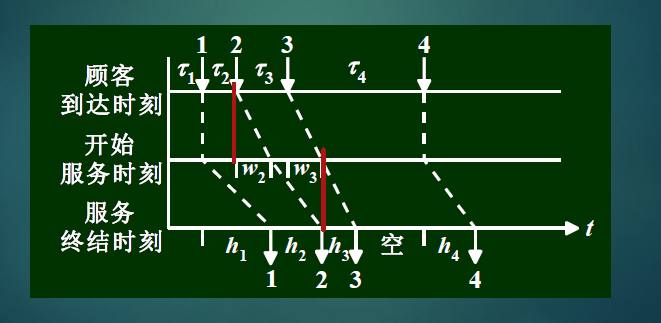
- 当服务台连续不断服务时,有如下关系:
w i + 1 + τ i + 1 = w i + h i w_{i+1}+\tau_{i+1}=w_i+h_i wi+1+τi+1=wi+hi
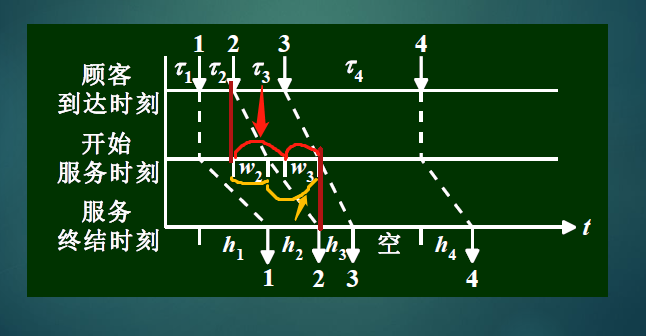
- wi+hi 表示了累计的未完成的服务时长,一般地有
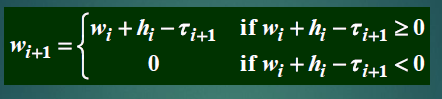
tips:排队系统的指标及其关系
1)Wq 、Wd 分别是顾客的平均排队等待时间和平均逗留时间
2)Lq 、Ld分别是系统平均排队的顾客数和系统的平均顾客数
3) Ln 是同时接受服务的平均顾客数(即平均服务台占用数)
4) h 是顾客的平均服务时长,λ是顾客的平均到达率(即单位时间内到达的顾客数)。
5)相关公式
L
d
=
λ
W
d
=
λ
(
W
q
+
h
)
=
L
q
+
L
n
Ld = \lambda W_d= \lambda(W_q + h ) = L_q + L_n
Ld=λWd=λ(Wq+h)=Lq+Ln
L q = λ W q Lq = \lambda W_q Lq=λWq
L n = λ h L_n = \lambda h Ln=λh
7.3 服务时间与间隔时间
7.3.1 概述
- 顾客的服务时间由于多种原因具有不确定性,最好的描述方法就是概率分布;同样顾客到达的间隔时间也具有一定的概率分布
- 服务时间和到达间隔时间服从什么分布?可以先通过统计得到经验分布,再做理论假设和检验。
- 经验分布一般采用直方图来表示,如下图
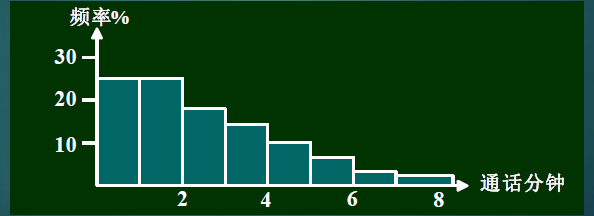
下述内容是之前概率论学过的
主要是讲述

7.3.2 常用的概率分布
- 定长分布
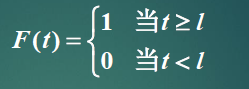
- 负指数分布(重点)

- 爱尔兰分部

7.3.3 负指数分布的特点
-
负指数分布之所以常用,是因为它有很好的特性,使数学分析变得方便: 期望等于均方差
-
无记忆性 。指的是不管一次服务已经过去了多长时间,该次服务所剩的服务时间仍服从原负指数分布
证明

- 普通型:多个独立同分布负指数分布的服务在进行,不可能有两个以上同时结束
证明

7.4 输入过程
顾客到达的分布,可用相继到达顾客的间隔时间描述,也可以用单位时间内到达的顾客数描述
-
定长输入过程:间隔时间服从定长分布
-
泊松输入过程:单位时间内到达的顾客数服从泊松分布
7.4.1 泊松输入过程及其特点
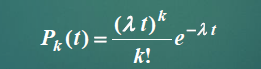
泊松分布的均值和方差均为λ , λ也称为到达率, λt 是(0, t) 时间内顾客到达的期望值
-
平稳性 :顾客到达数只与时间区间长度有关
-
无后效性 :不相交的时间区间内所到达的顾客数是独立的
-

-
有限性 :在有限的时间区间内,到达的顾客数是有限的。
-
可叠加性:即独立的泊松分布变量的和仍为泊松分布(概率论)

- 泊松过程的到达间隔时间为负指数分布
证

7.4.2 马尔科夫链
马尔科夫链 (Markov Chain ) 又简称马氏链 ,是一种 离散事件 随机过程。
用数学式表达为:
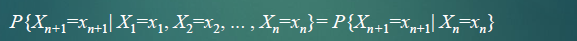
- X n+ 1 的状态只与 X n 的状态有关,与 X n 前的状态无关,具有无记忆性或 无后效性 ,又称 马氏性
- 状态转移是一步一步发生的(从i状态转移到j状态)。令 X n = i 表示系统在时刻 t 处于状态 i 这一事件,一步状态转移概率:
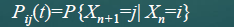
7.5 生灭过程
一种描述自然界生灭现象的数学方法,如细菌的繁殖和灭亡、人口的增减、生物种群的灭种现象等
- 采用马氏链
- 令 N t 代表系统在时刻 t 的状态,下一瞬间 t = t 系统的状态只能转移
- 到相邻状态,或维持不变,如图所示:数量 +1 数量 1 ,数量不变
- 三种转移是不相容的,三者必居其一
- 只有具有无记忆性和普通性的过程 分布 才适用马氏链
- 令 P j(t) P{ N(t) = j }代表系统在时刻 t 处于状态 j 的概率

- 生灭过程的马氏链
推导过程了解即可
-
首先解稳态方程组

-
其次解递归解
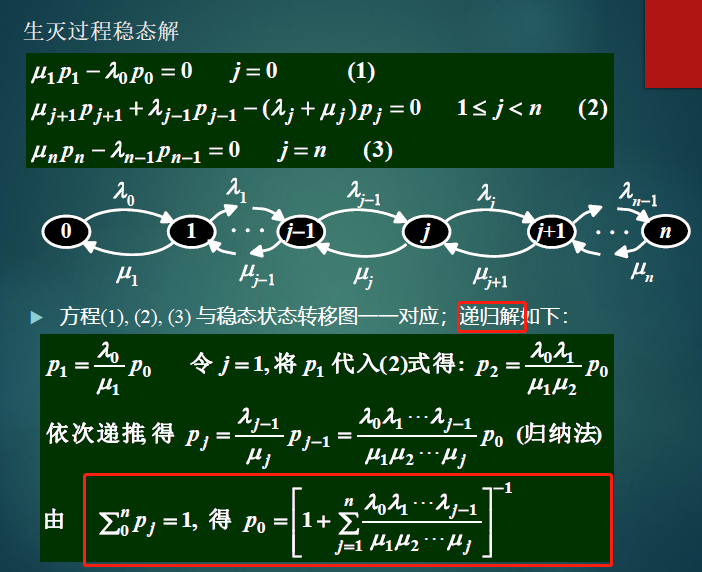
- 满足生灭过程的条件

第八章 M/M/n系统
泊松输入/负指数服务时长/n个并联服务台
8.1 M/M/n损失制
增长:有新来的顾客
消亡:有顾客完成服务
8.1.1 M/M/n损失制,无限源
顾客到达率:λ(人/小时)
每个台的服务率(人/小时):
化简:ρ=λ/μ称为业务量,表示一个平均服务一个人到几个人

-
系统的服务质量
系统的质量用损失率来度量,两种度量方法

服务台利用率
(1-B):完成服务率

-
求所需最少服务台的方法

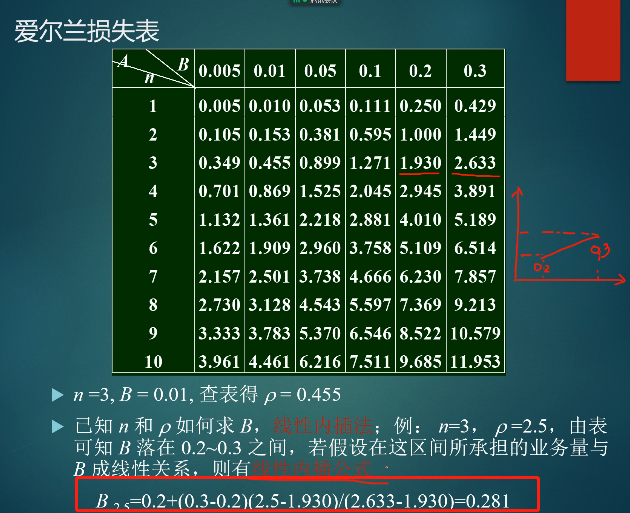
- 爱尔兰损失表
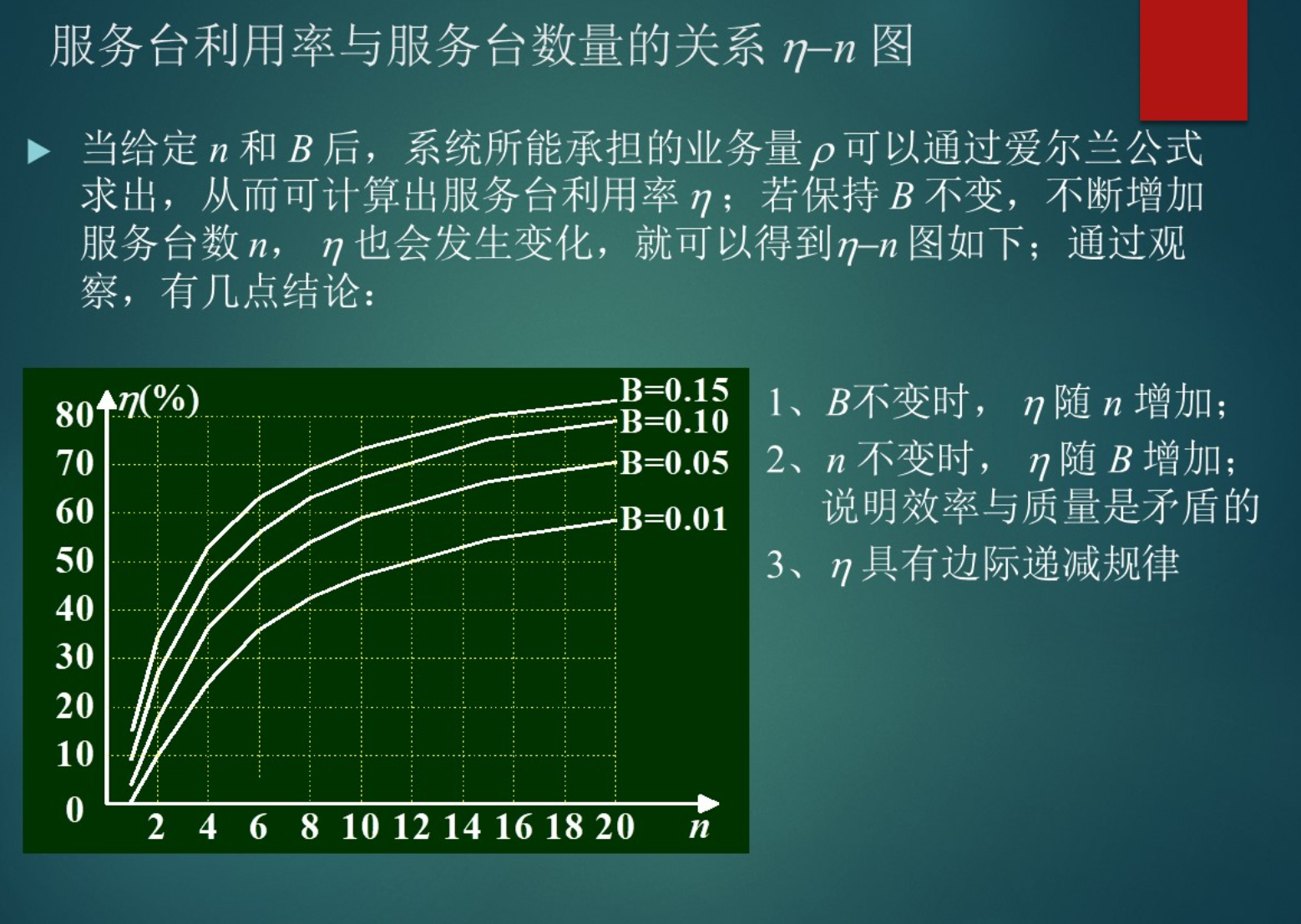
- 服务台利用率和服务台数量的关系
例 1:

解

例 2:

解


例 3:

解

8.1.2 M/M/n损失制,有限源
顾客到达率是与系统中被服务的顾客数相关的
N:顾客总数
n:服务台个数
j:现在服务的人数
**q=γ/μ:**平均时长

- 衡量服务质量的指标:损失率
按时间计算的损失率:
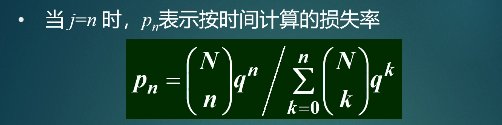
按顾客到达的损失率:

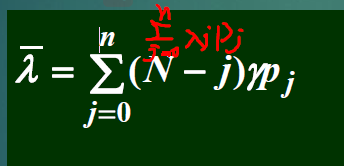
不用记,考试要用会给
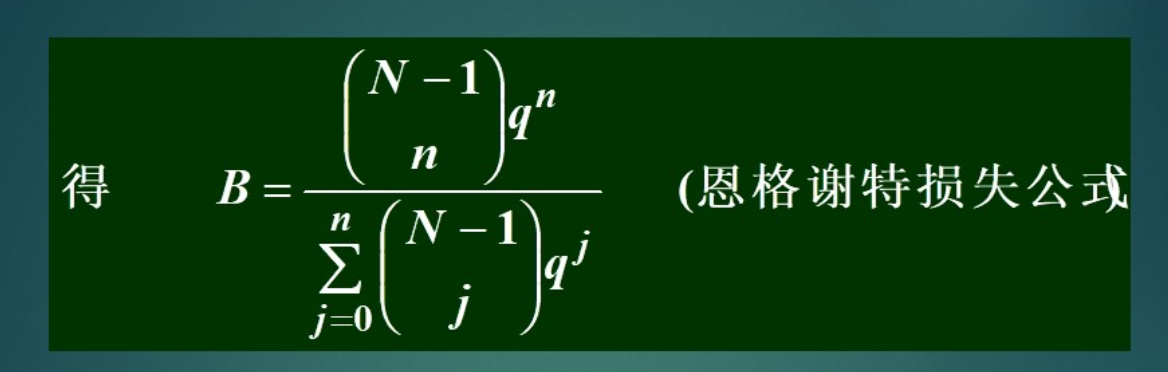
- 服务台利用率
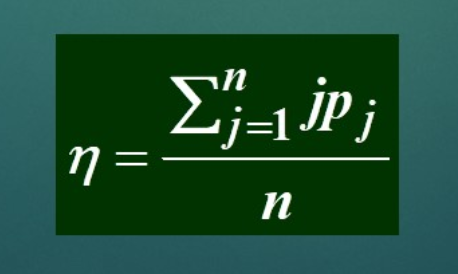
例1:

解
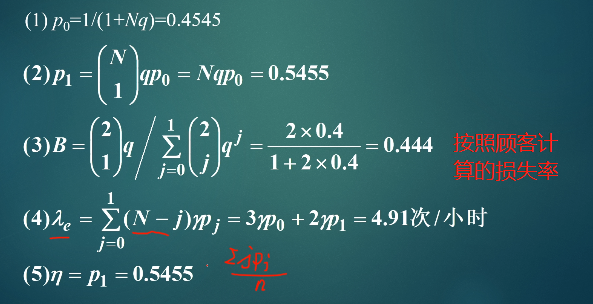
8.2 M/M/n等待制,无限源,无限容量
8.2.1 系统稳态概率及等待概率
顾客到达率为λ
每台的服务率为μ
业务量:ρ=λ/μ
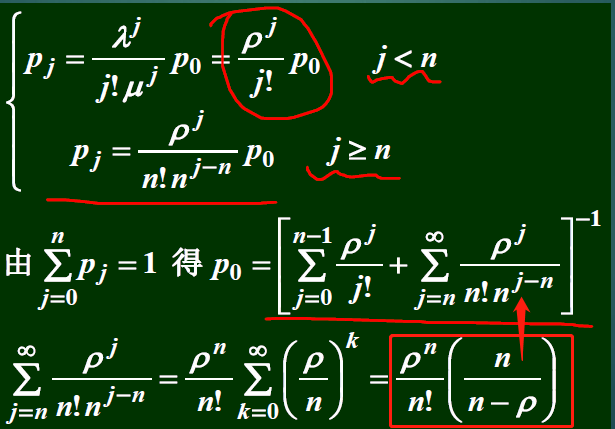
- 计算顾客进入系统必须等待的概率D
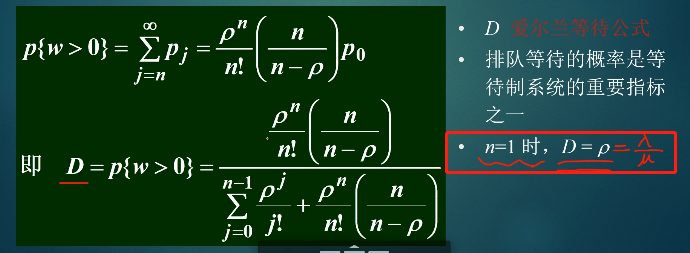
8.22 系统的各个指标
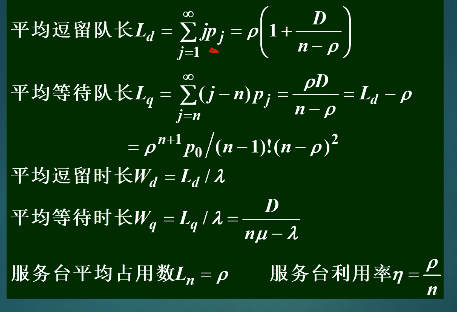
当n=1时
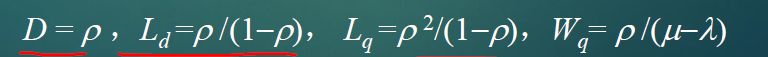
8.23 系统等待时间的分布概率
顾客离去的概率符合泊松分布:


tips:
做题时关注n=1,如果有,可以简化做题
例1:



例2:


第九章 存储理论
9.1 简单介绍
存储理论主要分为:

我们只关注 经典存储理论
- 术语



- 存储策略
9.2 确定性存储模型
市场的备运期和需求是已知的
9.2.1 不允许缺货模型
Cd:一次性订购费
Cs:单位时间存储费
t:订货周期


C(Q):单位时间内的可变费用
- 定量分析:
Q = D t :每次订购量 Q=Dt:\text{每次订购量} Q=Dt:每次订购量
平均存储量 = 1 / 2 Q 平均存储量=1/2Q 平均存储量=1/2Q
单位时间存储费:三角形面积/t*单位时间存储费

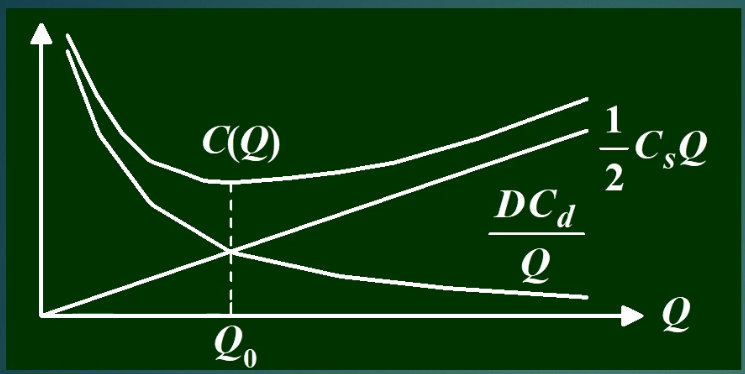
(必考)
Q0:最佳经济订货量
C(Q0):最佳费用
t0:最佳订货周期

几点说明:

例题:

解
计算年存储费使用的是:平均存储量

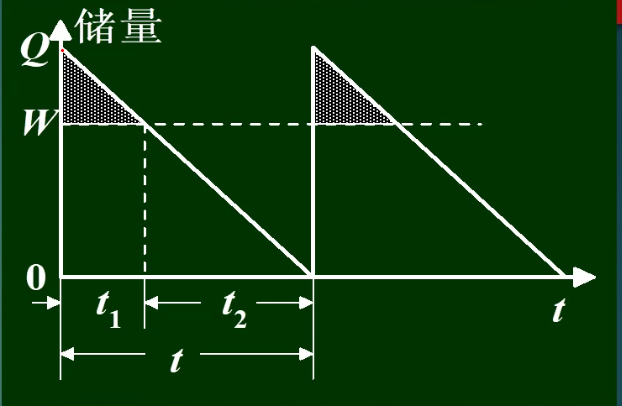
9.2.2 允许缺货模型
H:最大存储量
Cq:单位缺货损失费
缺货时间:t2



例:

解

9.2.3 连续进货,不允许缺货模型
t1:零件生产期
K:零件生产率,D:零件消耗率
Cd:准备费
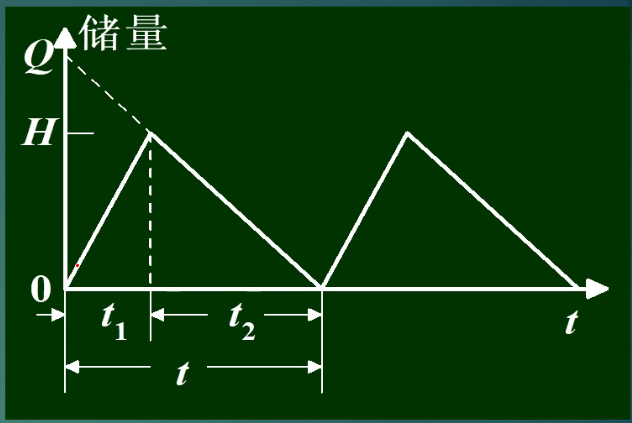
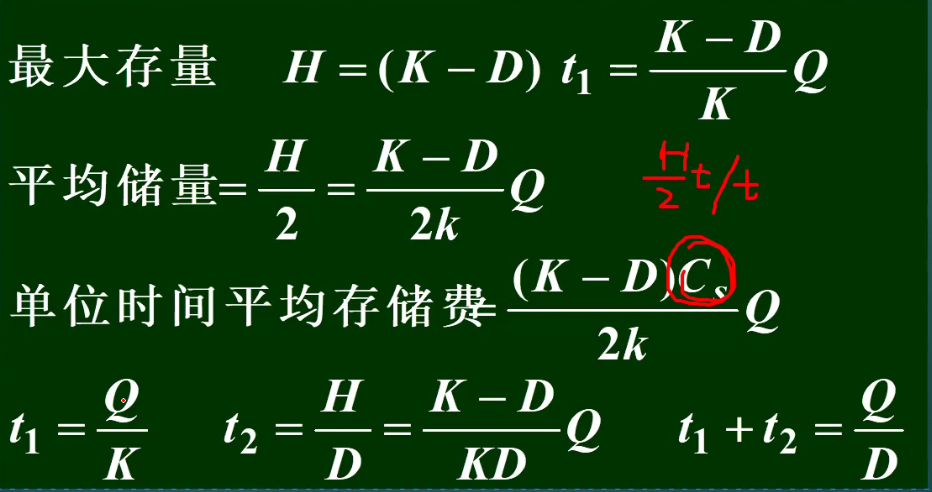

直接代入不缺货模型公式(3):
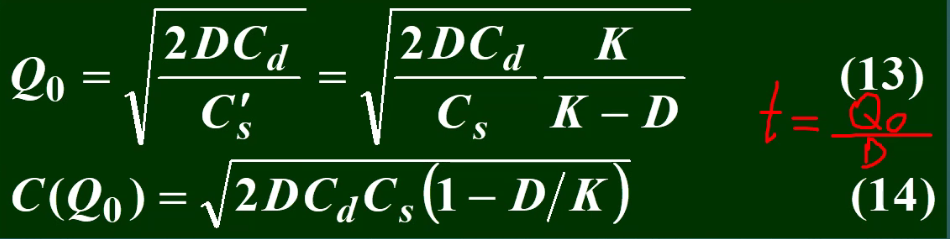
9.2.4 两种存储费,不允许缺货模型
自己仓库存储量不够,租用其他仓库


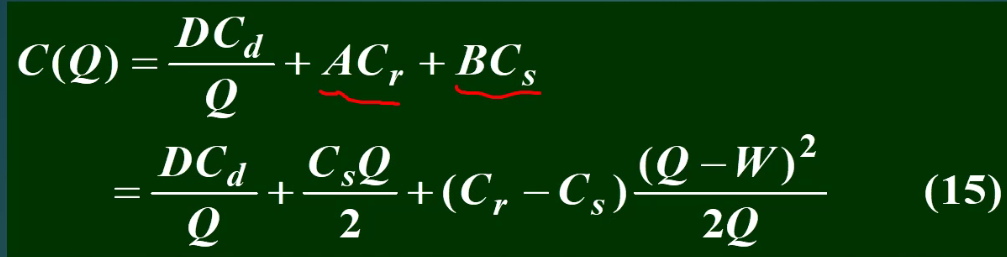

9.2.5 不允许缺货,批量折扣模型
购买越多,单价越低
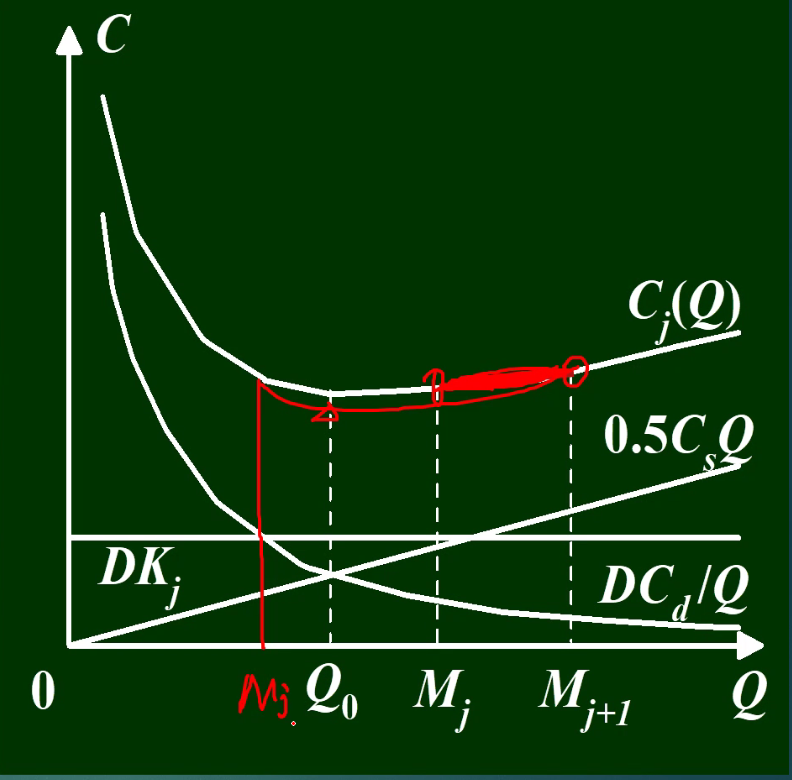

在区间内的价格公式:
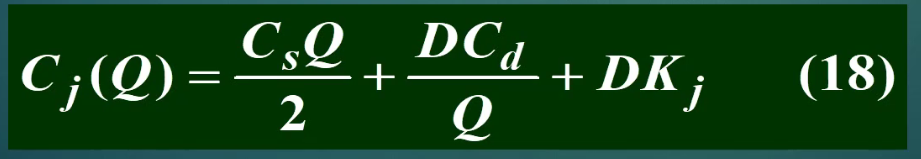
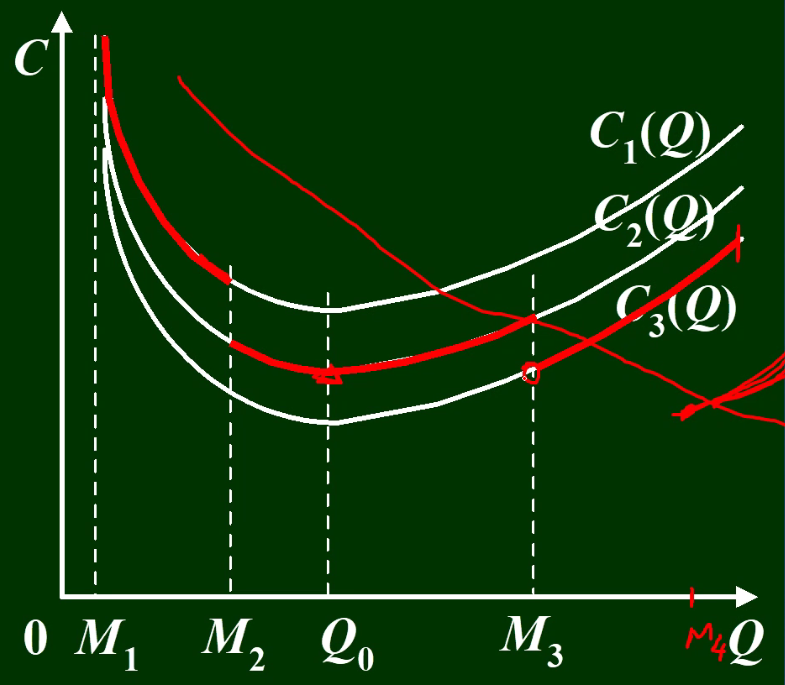
Q0是否为最小值要与右边区间(左端点)进行比较
计算步骤:

例:

解
要计算每个区间的右端点,算出最小值C(Q0)

考试范围: