前言：
大家好，我是良辰丫，今天和大家一起讨论一下时间复杂度与空间复杂度，往往来说，这两者是衡量算法好坏的标准，举个简单的例子，你想吃核桃了，用牙能弄开，用夹子也能弄开，但是用工具效率更高一些，于是乎，为了研究算法的效率，计算机领域的科学家们引入了时间复杂度和空间复杂度，那么这二者到底是什么呢？我们接下来往下看。🚀🚀🚀

🧑个人主页：良辰针不戳
📖所属专栏：java数据结构
🍎励志语句：生活也许会让我们遍体鳞伤，但最终这些伤口会成为我们一辈子的财富。
💦期待大家三连，关注，点赞，收藏。
💌作者能力有限，可能也会出错，欢迎大家指正。
💞愿与君为伴，共探Java汪洋大海。

---

---

1、衡量算法的标准

所谓算法，是解决问题的思路，比如高斯，从1加到100，一个一个加也能算出来，然后用高斯的公式也能算出来，然而呢，很显然，一个一个加效率显然不高。随着时间推移，计算机科学家们退出了两种衡量算法的标准，时间效率和空间效率，也就是我们口中的时间复杂度和空间复杂度。

• 程序的运行时间。（时间复杂度）
• 程序运行所需内存空间的大小。（空间复杂度）

2、时间复杂度

有的小伙伴可能会疑惑了，同样的程序在不同的电脑上，由于网速，电脑显卡好坏，CPU运行速率等因素，程序所运行的时间不一样，那么怎么才能计算时间呢？科学家们想出来了先分别计算程序中每条语句的执行次数，然后用总的执行次数间接表示程序的运行时间。

一些时间复杂度图

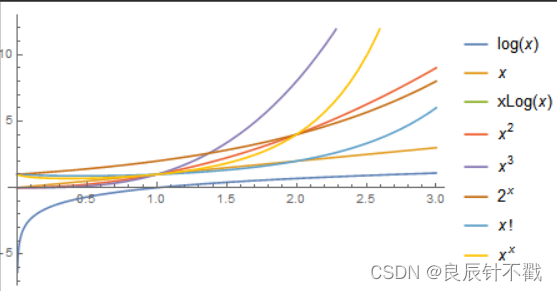
注意：

• 通常情况下我们说的时间复杂度是最坏情况下的时间复杂度，如果研究最好情况下，那没有意义。
• 我们描述时间复杂度用大O渐进表示法，比如O(n)。

接下来我们通过几个例子更深刻认识一下时间复杂度。

1. 下面代码执行了n次，我们就说它的时间复杂度为O(n)。

for(int i = 0 ; i < n ; i++)     // 从 0 到 n，执行 n+1 次
{
      System.out.println("叶良辰");  // 从 0 到 n-1，执行 n 次
}

2. 下面代码执行了n+520次，我们可以说它的时间复杂度为O(n + 520)，但是呢，当n趋近于无穷大的时候，520又显得很渺小，我们通常记做O(n)，因此呢，n后面有常数项，直接省略就可以。

for(int i = 0 ; i < n + 521 ; i++)     
 {
      System.out.println("叶良辰");  
 }

3. 下面代码大约执行了2 * n 次，我们把它记做 O(2n)，一般而言，当变量n前面有系数时我们不记录系数，n无穷大时，n和2n也就不会划分那么细了，因此呢，我们把它记为O(n)。

for(int i = 0 ; i < 2 * n ; i++)
 {
      System.out.println("叶良辰");
 }

4. 如果遇到了常数次数，我们直接记为O(1)就可以了。

for(int i = 0 ; i < 521 ; i++)
{
    System.out.println("叶良辰");
 }

5. 下面的运行次数为m + n 次，有的小伙伴可能就会说了，我们记做 O(m) 或者 O(n) 不是都行嘛？大家可以这样想，把n和m当成一个整体，他们两个合起来可能才趋近于无穷，因此呢，大家特别关注一下这个，时间复杂度为O(m + n)。

for(int i = 0 ; i < m + n ; i++)
{
      System.out.println("叶良辰");
}

6. 函数中含有相同变量，并且含有常数时，只保留最高阶变量。下面的时间复杂度就是n * n。

for(int i = 0 ; i < n * n + n + 5; i++)
{
      System.out.println("叶良辰");
}

小结:

• 函数中含有相同变量，并且含有常数时，只保留最高阶变量。
• 用O(1)表示运行次数为常数的时间复杂度。
• 变量的系数通常省略，例如2 * n * n时间复杂度为O(n * n)。

3、空间复杂度

鱼和熊掌不可兼得，时间复杂度和空间复杂度往往不可能全部做到最优，我们常常采用空间效率换时间效率，如果省下了空间，然而时间很慢，比如你上网玩游戏，空间内存做到最优了，但是时间很慢，那么游戏就会显得特别卡，我并不是说空间效率不重要，比起时间效率，空间效率显得更逊色。但是呢，我们还是需要去理解一下空间效率。

空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度 。空间复杂度不是程序占用了多少bytes的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟时间复杂度类似，也使用大O渐进表示法。

通过例子简单说明一下空间复杂度。

1. 下面只有一个变量，我们就可以说它的空间复杂度为O(1)。

     int num = 520;
     System.out.println(num);

2. 下面为求n的阶乘代码，函数没开辟一次栈帧，就需要开辟一次空间，因此呢递归一次开辟一次空间，该代码的空间复杂度为O(n)。

long factorial(int N) {
   return N < 2 ? N : factorial(N-1)*N;
}

后序：
读了这篇文章，想必大家对时间复杂度和空间复杂度有了一定的了解，期待大家的点赞三连，我们下次再见。💞💞💞