一命通关二分搜索

二分法

简介

和双指针一样，二分法也是一种优化方法，或者说二分法就是双指针的一类。不过，二分法的思想比双指针诞生更早也更广泛，在我们日常生活里也无时不刻在使用二分的思想。

比如我们想回顾某些影片，但是只记得影片的大概日期，我们往往会翻到最后一页，根据最后一页的日期再来取中估算出想找的影片可能对应的页数，通过不断重复来不断去定位影片的位置。

对于我们正常人来说，这种索引是灵活的，我们可以根据自己的需求来灵活调整二分的方法。
比如最后一页是100，我们在脑海里估算的时候，如果影片比较早，我们可能会定位到70页；如果影片是最近才出的，我们可能会定位到30页

但是，对于计算机，二分的算法是无法在程序进行的过程中调整的。也正因如此，二分会带来很多细节上的问题——死循环，越界等等，这也是二分最令人头疼的地方。但是二分作为一个将时间复杂度O(n)降为O(log n)的方法，在很多题中都作为了普遍的优化方法，所以单单研究出二分不是为了解决某种具体的问题，而是为将二分的思想运用到很多场景中。

朴素二分

朴素二分，就是我们在初学很多语言，第一次接触到的二分。

举一个很简单的例子704. 二分查找 - 力扣（LeetCode）

从一个有序数组中找到某个确定的值，最简单暴力的方法就是直接遍历，时间复杂度O(n)。但是从双指针的思想里，我们很容易发现，我们可以一边搜寻，一边排除。

比如我们想找到5这个元素，我们一开始便随便选一个元素下标，假设我们选择了元素9的下标。

找到9以后，将9和目标值比较，显然9是比5要大的。但是数组又是升序，我们就不需要考虑9以后的元素，只用在9前面的元素中再去找5。这样做的好处是什么？这样做显然将时间复杂度缩小了一半。
而我们不断重复这个过程，时间复杂度不断缩减为一半，最终时间复杂度就降为了O(log n)

同时，用某种方法可以证明，每次随便选择的数选择最中间的那个数，期望效率是最高的，具体证明方法就不解释了，因为我也不会。

简单用代码实现一下

int l=0;//左边界，从0开始
int r=nums.size()-1;//右边界，从最后一个元素开始

while(l<=r)//循环条件：左边界在右边界左边
{
    int mid=l+(r-l)/2;//二分取中
    if(nums[mid]==target)//如果找到了，返回该下标
        return mid;
    else if(nums[mid]<target)//如果找到的数小于目标值，意味着mid和mid左边的值都不满足条件
        l=mid+1;//从mid右边继续寻找
    else//如果找到的数大于目标值，意味着mid和mid右边的值都不满足条件
        r=mid-1;//从mid左边继续寻找
}
//如果循环结束了，代表所有数都不满足条件，那么退出循环返回-1

return -1;

但是，既然叫他朴素二分，那自然意味着朴素二分只能解决一小部分问题。朴素二分太过老实了，只要问题场景一换，那么朴素二分就会出很多bug

把例子稍微换一下：

边界二分

此时发现，我们最朴素的二分已经不够用了。但是，是不是二分就完全用不上了呢？

在这里，纠正一个很多人最常见的误区：

二分不是只有数组顺序的时候才可以使用，

而是只要数组能满足区间规律，

就可以用二分来解决。

就比如在这里，虽然朴素二分用不上了，但是因为数组还是满足一个条件：

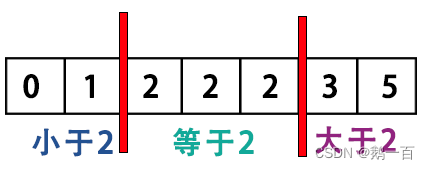
所以还是可以根据二分的思想，来找到每一个区间。

此时，我们想找到等于二的左区间，我们还是取二分中值的元素，发现等于2

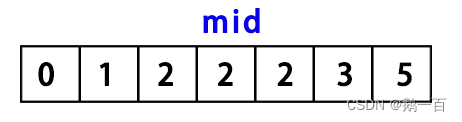
这也代表着，我们找到了等于2的区间中的一个元素，但是这却不一定是左边界，因为这个2可能会有三种情况：

为左边界
为中间的某个元素
为右边界

不过，无论是哪一种情况，都会对应一个结果：mid右边一定不存在我们想找的左边界，我们让right=mid，再来进行一次寻找。

但是，为什么right不能等于mid-1?因为mid可能就是左边界，如果right等于mid-1，那么就越过了左边界找不到结果。

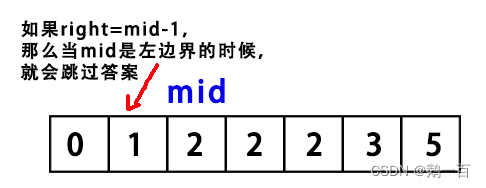
所以，我们可以轻易得到 $if(nums[mid]==2) right=mid$

再来看其他两种情况：
如果mid对应的元素小于target，那答案一定在mid的右边，也就是
$if(nums[mid]<2) left=mid+1$
如果mid对应的元素大于target，那答案一定在mid的左边，也就是
$if(nums[mid]>2) right=mid-1$

不过这里还有一个坑点：while循环的条件是什么？

我们来看这个情况：

所以，结束条件只能是：l<r

用代码实现一下：

int l=0;
int r=nums.size();

while(l<r)
{
    int mid=l+(r-l)/2;
    
    if(nums[mid]<target)
        l=mid+1;
    else
        r=mid;//因为r=mid-1和r=mid效率几乎没有区别，所以合并成同一种情况
}

return l;//出循环的时候一定是l==r，所以返回哪一个都无所谓

右边界二分

再把问题变一下

此时上面的方法又行不通了，不过思考的方式还是一样的。

我们找到一个二分中值mid，可能有三种情况：

nums[mid]==target，那右边界一定不在mid右边
nums[mid]<target，那右边界一定在mid右边
nums[mid]>target，那右边界一定在mid左边

总结下来还是那三种：

if(nums[mid]>target)
    r=mid-1;//如果mid对应的值大于，那么往左边找
else
    l=mid;//和找左边界情况一样，为了避免跳过答案，所以一定不能为mid+1

那是不是就这么简单解决了呢？当然不是，这又出现了一个新的坑点：

怎么解决这个问题？也很简单，mid=left+(right-left+1)/2就行了。

因为产生这个问题的根本原因，就是当left和right相邻的时候，mid应该是取left还是取right。我们直接从判断式来看

左边界是r=mid，但是为了避免死循环，r一定要产生改变，所以mid一定不能取r
右边界是l=mid，但是为了避免死循环，l一定要产生改变，所以mid一定不能取l

所以在这里，我们的mid一定要取right对应的值，而这个问题说人话就是，向下取整和向上取整的问题。

用代码实现一下：

int l=0;
int r=nums.size();

while(l<r)
{
    int mid=l+(r-l+1)/2;//向上取整
    
    if(nums[mid]>target)
        r=mid-1;
    else
        l=mid;
}

return l;//出循环的时候一定是l==r，所以返回哪一个都无所谓

边界总结和模板

说了这么多，左边界和右边界其实有着很大的共性：

循环条件一定是l<r
出循环的时候，最终都会为l==r，无论返回哪一个都一样

但是，我们怎么判断左边界和右边界的区别？什么时候用什么代码？

其实只需要考虑两个问题：

1.是大于等于还是大于

我们来看一下右边界情况的语言描述：

不在右边，也就是>=，代表着包含着当前的元素，也就对应着l=mid
在右边和在左边，也就是>和<，代表着不包含当前的元素，也就对应着l=mid+1和r=mid-1

而说白了，也就是个最简单的数学表达式描述问题，我们只需要看着文字，然后转换成数学式，小学生都会。

2.向上还是向下取整来避免死循环

在右边界二分的时候，就已经详细说明了，我们取mid的不同其实就是为了避免进入死循环，而解决方法就是通过判断是l=mid还是r=mid，来分别向上取整和向下取整。

所以，最终可以总结出求左右边界的模板：

int l=0;
int r=nums.size();

while(l<r)
{
    1.判断mid是向上取整还是向下取整
    
    2.列出三种情况，然后分别转化成两个数学判断表达式
}

return l;

所有二分问题都可以通过这个模板来解决。

而看完了这些，再去尝试这道题，只有自己亲自动手理解和解出来，才表示完全掌握了二分模板。

34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣（LeetCode）https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/description/