二叉树——700. 二叉搜索树中的搜索、98. 验证二叉搜索树

news2024/10/6 16:18:49

二叉搜索树中的搜索

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。返回以该节点为根的子树。如果节点不存在，则返回 null 。

示例 1:
在这里插入图片描述

输入：root = [4,2,7,1,3], val = 2
输出：[2,1,3]
示例 2:

重点

1. 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值
2. 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值
3. 它的左、右子树也分别为二叉搜索树

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
        if root == None:
            return None
        if root.val == val:
            return root
        elif root.val > val:
            return self.searchBST(root.left, val)
        elif root.val < val:
            return self.searchBST(root.right, val)

验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

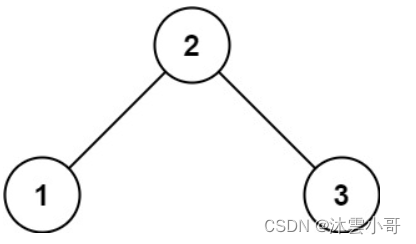
在这里插入图片描述

输入：root = [2,1,3]
输出：true

重点

二叉搜索树中序遍历满足 “ 持续递增 ” 的规律。
1. 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
2. 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
3. 它的左、右子树也分别为二叉搜索树

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def __init__(self):
        self.vec = []
    def traversa1(self, root):
        if root == None:
            return 
        self.traversa1(root.left)
        self.vec.append(root.val)
        self.traversa1(root.right)
    def isValidBST(self, root: Optional[TreeNode]) -> bool:
        self.vec = []
        self.traversa1(root)
        for i in range(1, len(self.vec)):
            if self.vec[i] < self.vec[i-1]:
                return False
        return True