目录
235.二叉搜索树的最近公共祖先
701.二叉搜索树的插入操作
450.删除二叉搜索树中的节点
669.修建二叉搜索树
108.将有序数组转换为二叉搜索树
538.把二叉搜索树转换为累加树
235.二叉搜索树的最近公共祖先
235. 二叉搜索树的最近公共祖先
中等
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
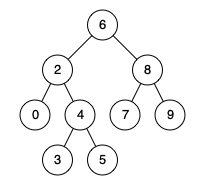
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8 输出: 6 解释: 节点2和节点8的最近公共祖先是6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4 输出: 2 解释: 节点2和节点4的最近公共祖先是2, 因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉搜索树中。
如果 中间节点是 q 和 p 的公共祖先,那么 中节点的数组 一定是在 [p, q]区间的。即 中节点 > p && 中节点 < q 或者 中节点 > q && 中节点 < p。
那么只要从上到下去遍历,遇到 cur节点是数值在[p, q]区间中则一定可以说明该节点cur就是p 和 q的公共祖先。
如图,我们从根节点搜索,第一次遇到 cur节点是数值在[q, p]区间中,即 节点5,此时可以说明 q 和 p 一定分别存在于 节点 5的左子树,和右子树中。
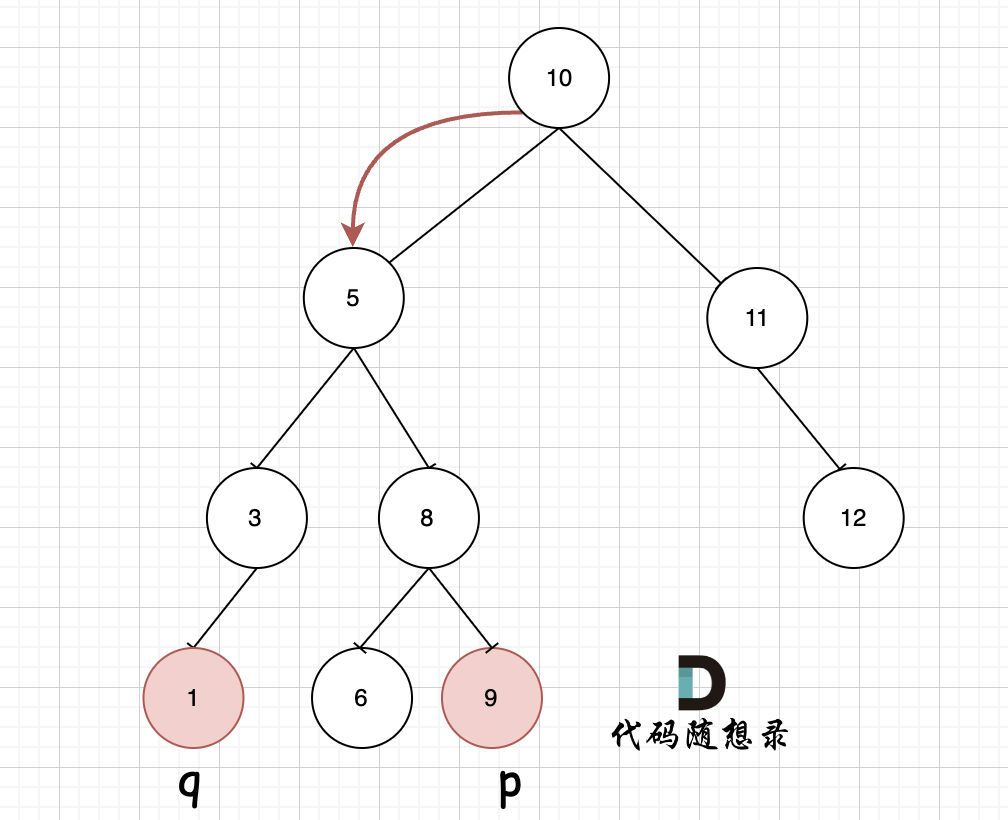
此时节点5是不是最近公共祖先? 如果 从节点5继续向左遍历,那么将错过成为p的祖先, 如果从节点5继续向右遍历则错过成为q的祖先。
所以当我们从上向下去递归遍历,第一次遇到 cur节点是数值在[q, p]区间中,那么cur就是 q和p的最近公共祖先。
/**
* Definition for a binary tree node.
* 定义了一个二叉树的节点类。
* public class TreeNode {
* int val; // 节点的值
* TreeNode left; // 指向左子节点的指针
* TreeNode right; // 指向右子节点的指针
* TreeNode(int x) { val = x; } // 构造函数,用于创建一个新节点,并设置其值为x
* }
*/
class Solution {
// 在二叉搜索树中找到节点p和q的最低公共祖先
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
// 如果根节点为空,表示当前子树不包含p和q,返回null
if(root == null){
return null;
}
// 如果根节点的值大于p和q的值,说明p和q(如果存在)一定在左子树中
if(root.val > p.val && root.val > q.val){
// 递归地在左子树中查找p和q的最低公共祖先
TreeNode leftResult = lowestCommonAncestor(root.left,p,q);
return leftResult;
}
// 如果根节点的值小于p和q的值,说明p和q(如果存在)一定在右子树中
if(root.val < p.val && root.val < q.val){
// 递归地在右子树中查找p和q的最低公共祖先
TreeNode rightResult = lowestCommonAncestor(root.right,p,q);
return rightResult;
}
// 如果根节点的值位于p和q的值之间,说明p和q分别位于根节点的左右两侧
// 因此,当前根节点就是p和q的最低公共祖先
return root;
}
}迭代法:
class Solution {
// 定义Solution类
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
// 定义方法lowestCommonAncestor,接收三个参数:BST的根节点root,以及要查找的两个节点p和q
while(root != null){
// 当根节点不为null时,进行循环查找
if(root.val > p.val && root.val > q.val){
// 如果当前根节点的值大于p和q的值
root = root.left;
// 则最低公共祖先一定在左子树中,将root指向左子节点,继续查找
}
else if(root.val < p.val && root.val < q.val){
// 如果当前根节点的值小于p和q的值
root = root.right;
// 则最低公共祖先一定在右子树中,将root指向右子节点,继续查找
}
else{
// 如果当前根节点的值介于p和q的值之间
// 这意味着p和q分别在根节点的左右两侧或者其中一个是根节点本身
return root;
// 返回当前根节点作为最低公共祖先
}
}
// 如果root为null,说明已经遍历完整个树但没有找到p和q
// 这可能是因为p和q不在树中,或者树的构建有问题
return null;
// 返回null表示没有找到最低公共祖先
}
}701.二叉搜索树的插入操作
701. 二叉搜索树中的插入操作
中等
给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。
示例 1:
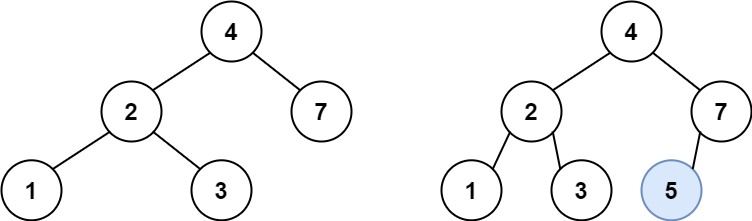
输入:root = [4,2,7,1,3], val = 5 输出:[4,2,7,1,3,5] 解释:另一个满足题目要求可以通过的树是:
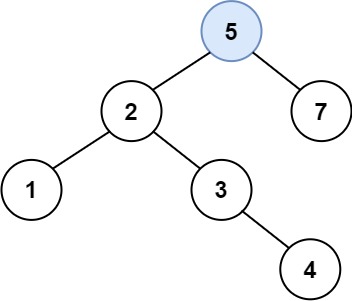
示例 2:
输入:root = [40,20,60,10,30,50,70], val = 25 输出:[40,20,60,10,30,50,70,null,null,25]
示例 3:
输入:root = [4,2,7,1,3,null,null,null,null,null,null], val = 5 输出:[4,2,7,1,3,5]
提示:
- 树中的节点数将在
[0, 104]的范围内。 -108 <= Node.val <= 108- 所有值
Node.val是 独一无二 的。 -108 <= val <= 108- 保证
val在原始BST中不存在。
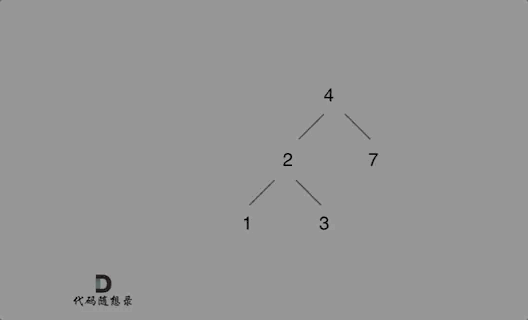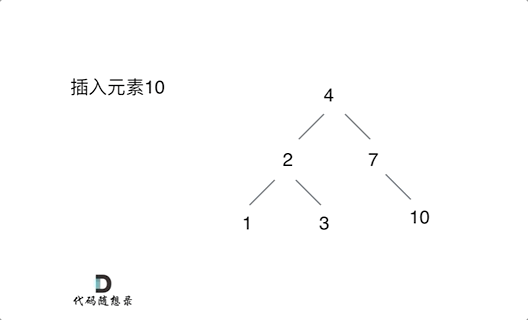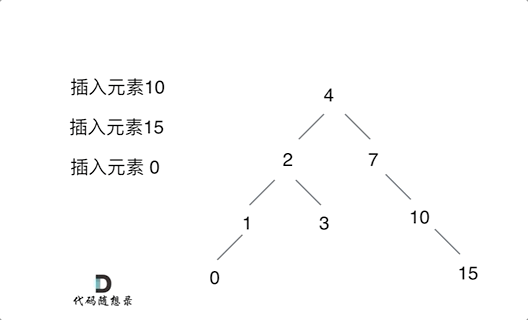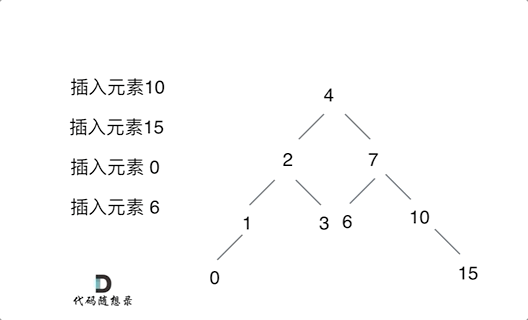
思路就是每插入一个元素,都可以把该元素放到根节点中,所以要根据插入节点的大小找到叶子节点,下一步遇到null的时候直接将元素的大小将该元素插入该叶子节点的左节点或者右节点
递归法:
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
if (root == null) {
// 如果当前节点为空,说明找到了合适的位置来插入新节点
return new TreeNode(val);
}
if (root.val < val) {
// 如果当前节点的值小于要插入的值,说明新节点应该插入到右子树中
root.right = insertIntoBST(root.right, val);
} else if (root.val > val) {
// 如果当前节点的值大于要插入的值,说明新节点应该插入到左子树中
root.left = insertIntoBST(root.left, val);
}
// 返回更新后的根节点
return root;
}
}迭代法:
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
// 如果根节点为空,则创建一个新的节点作为根节点,并返回这个新节点
if (root == null) return new TreeNode(val);
// 初始化 newRoot 为根节点,用于返回整个树的根节点
// pre 用于记录当前节点的前一个节点,即父节点
TreeNode newRoot = root;
TreeNode pre = root;
// 使用 while 循环遍历 BST,寻找插入新节点的合适位置
while (root != null) {
// 将当前节点赋值给 pre,以便后续操作
pre = root;
// 如果当前节点的值大于要插入的值,说明新节点应该插入到左子树中
if (root.val > val) {
root = root.left;
// 如果当前节点的值小于要插入的值,说明新节点应该插入到右子树中
} else if (root.val < val) {
root = root.right;
}
}
// 退出循环后,root 为 null,说明找到了插入新节点的位置
// 根据 pre 的值决定新节点是插入到左子树还是右子树
if (pre.val > val) {
// 如果 pre 的值大于要插入的值,说明新节点应该插入到 pre 的左子树中
pre.left = new TreeNode(val);
} else {
// 否则,新节点应该插入到 pre 的右子树中
pre.right = new TreeNode(val);
}
return newRoot;
}
}450.删除二叉搜索树中的节点
450. 删除二叉搜索树中的节点
中等
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
- 首先找到需要删除的节点;
- 如果找到了,删除它。
示例 1:
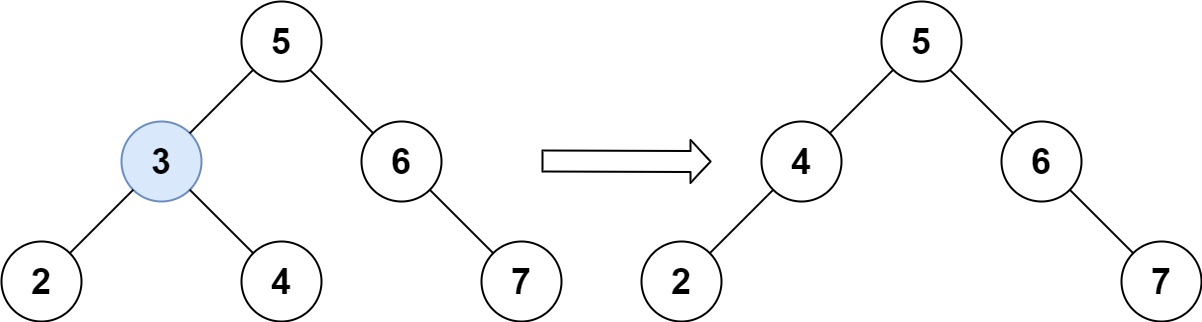
输入:root = [5,3,6,2,4,null,7], key = 3 输出:[5,4,6,2,null,null,7] 解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。 一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。 另一个正确答案是 [5,2,6,null,4,null,7]。
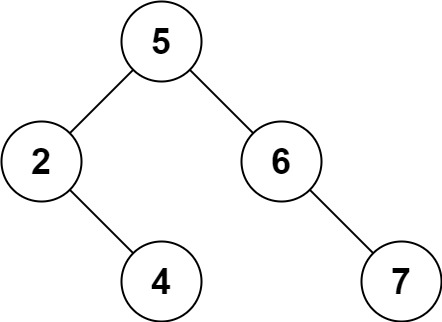
示例 2:
输入: root = [5,3,6,2,4,null,7], key = 0 输出: [5,3,6,2,4,null,7] 解释: 二叉树不包含值为 0 的节点
示例 3:
输入: root = [], key = 0 输出: []
提示:
- 节点数的范围
[0, 104]. -105 <= Node.val <= 105- 节点值唯一
root是合法的二叉搜索树-105 <= key <= 105
进阶: 要求算法时间复杂度为 O(h),h 为树的高度。
有以下五种情况:
- 第一种情况:没找到删除的节点,遍历到空节点直接返回了
- 找到删除的节点
- 第二种情况:左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点
- 第三种情况:删除节点的左孩子为空,右孩子不为空,删除节点,右孩子补位,返回右孩子为根节点
- 第四种情况:删除节点的右孩子为空,左孩子不为空,删除节点,左孩子补位,返回左孩子为根节点
- 第五种情况:左右孩子节点都不为空,则将删除节点的左子树头结点(左孩子)放到删除节点的右子树的最左面节点的左孩子上,返回删除节点右孩子为新的根节点。
第五种情况有点难以理解,看下面动画:
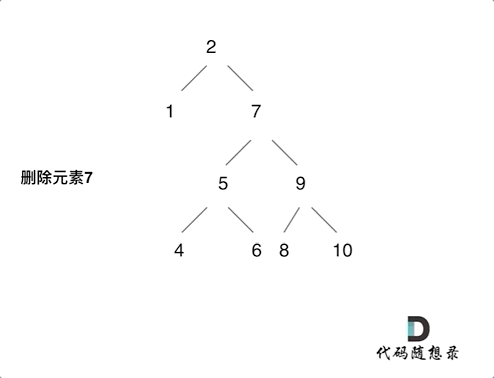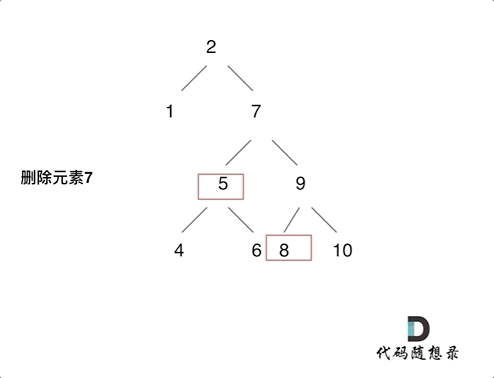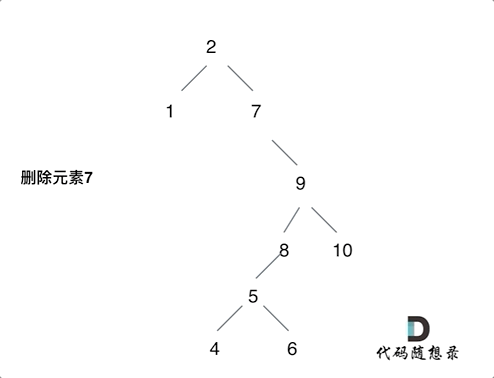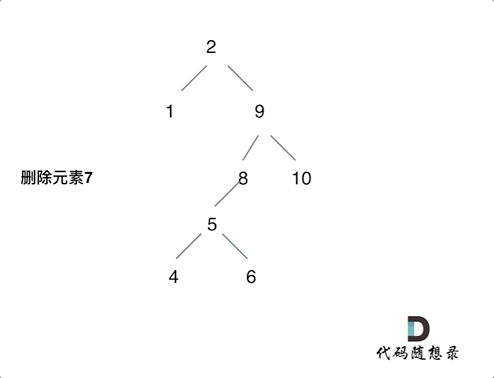
动画中的二叉搜索树中,删除元素7, 那么删除节点(元素7)的左孩子就是5,删除节点(元素7)的右子树的最左面节点是元素8。
将删除节点(元素7)的左孩子放到删除节点(元素7)的右子树的最左面节点(元素8)的左孩子上,就是把5为根节点的子树移到了8的左孩子的位置。
要删除的节点(元素7)的右孩子(元素9)为新的根节点。.
这样就完成删除元素7的逻辑,最好动手画一个图,尝试删除一个节点试试。
这里要删除7,需要找一个只比7大一点的元素,即中序遍历的话7的后一个元素,将7的左子树放在该节点左子树的位置上,这样才能保证删除之后的二叉树还是二叉搜索树
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
// 1.如果根节点为空,直接返回null
if(root == null){
return null;
}
// 如果找到了要删除的节点
if(root.val == key){
// 2.如果要删除的节点没有左右子节点,直接返回null
if(root.left == null && root.right == null){
return null;
}
// 3.如果要删除的节点只有右子节点,返回右子节点
else if(root.left == null && root.right != null){
return root.right;
}
// 4.如果要删除的节点只有左子节点,返回左子节点
else if(root.right == null && root.left != null){
return root.left;
}
// 5.如果要删除的节点既有左子节点又有右子节点
// 找到右子树中最小的节点(即最左边的节点)
else{
TreeNode cur = root.right;
while(cur.left != null){
cur = cur.left;
}
cur.left = root.left; // 将最小节点的左子树设为要删除节点的左子树
return root.right; // 返回新的节点(原要删除节点的右子树)
}
}
// 如果要删除的节点值小于根节点的值,说明要删除的节点在左子树中
if(root.val > key){
root.left = deleteNode(root.left,key); // 递归调用deleteNode方法删除左子树中的节点
}
// 如果要删除的节点值大于根节点的值,说明要删除的节点在右子树中
if(root.val < key){
root.right = deleteNode(root.right,key); // 递归调用deleteNode方法删除右子树中的节点
}
// 返回更新后的根节点
return root;
}
}669.修建二叉搜索树
669. 修剪二叉搜索树
中等
给你二叉搜索树的根节点 root ,同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即,如果没有被移除,原有的父代子代关系都应当保留)。 可以证明,存在 唯一的答案 。
所以结果应当返回修剪好的二叉搜索树的新的根节点。注意,根节点可能会根据给定的边界发生改变。
示例 1:
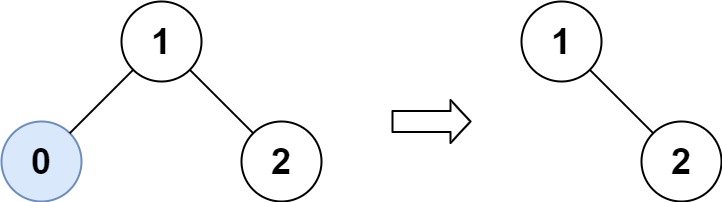
输入:root = [1,0,2], low = 1, high = 2 输出:[1,null,2]
示例 2:
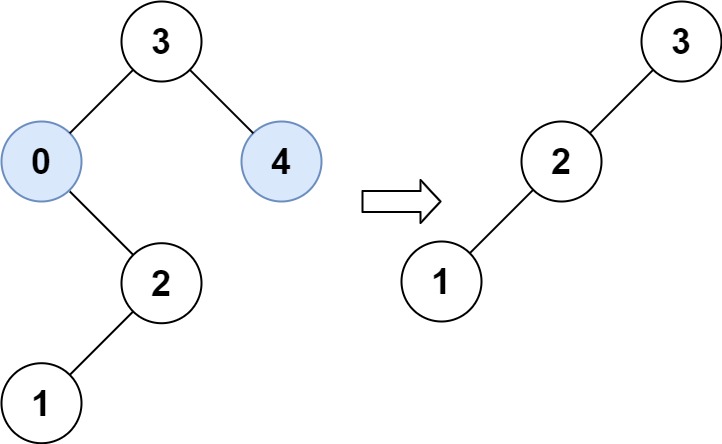
输入:root = [3,0,4,null,2,null,null,1], low = 1, high = 3 输出:[3,2,null,1]
提示:
- 树中节点数在范围
[1, 104]内 0 <= Node.val <= 104- 树中每个节点的值都是 唯一 的
- 题目数据保证输入是一棵有效的二叉搜索树
0 <= low <= high <= 104
class Solution {
public TreeNode trimBST(TreeNode root, int low, int high) {
// 如果根节点为空,则直接返回null
if(root == null){
return null;
}
// 如果根节点的值小于low,说明根节点及其左子树的所有节点值都小于low
// 因此,只需要修剪右子树,并返回修剪后的右子树作为新的根节点
//这里相当于直接删除了根节点和左子树
if(root.val < low){
return trimBST(root.right,low,high);
}
// 如果根节点的值大于high,说明根节点及其右子树的所有节点值都大于high
// 因此,只需要修剪左子树,并返回修剪后的左子树作为新的根节点
//这里相当于直接删除了根节点和右子树
else if(root.val > high){
return trimBST(root.left,low,high);
}
// 如果根节点的值在[low, high]的范围内,则需要同时修剪左右子树
// 修剪左子树时,要保证左子树中所有节点的值都大于等于low
// 修剪右子树时,要保证右子树中所有节点的值都小于等于high
// 修剪完成后,更新根节点的左右子树,并返回根节点
else{
root.left = trimBST(root.left,low,high);
root.right = trimBST(root.right,low,high);
}
// 返回修剪后的根节点
return root;
}
}108.将有序数组转换为二叉搜索树
108. 将有序数组转换为二叉搜索树
简单
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
示例 1:
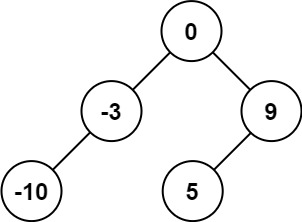
输入:nums = [-10,-3,0,5,9] 输出:[0,-3,9,-10,null,5] 解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:
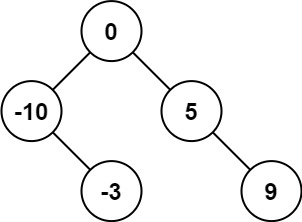
示例 2:
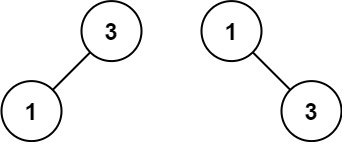
输入:nums = [1,3] 输出:[3,1] 解释:[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。
提示:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums按 严格递增 顺序排列
这里有一个问题:如果数组长度为偶数,中间节点有两个,取哪一个?
取哪一个都可以,只不过构成了不同的平衡二叉搜索树。
例如:输入:[-10,-3,0,5,9]
如下两棵树,都是这个数组的平衡二叉搜索树:
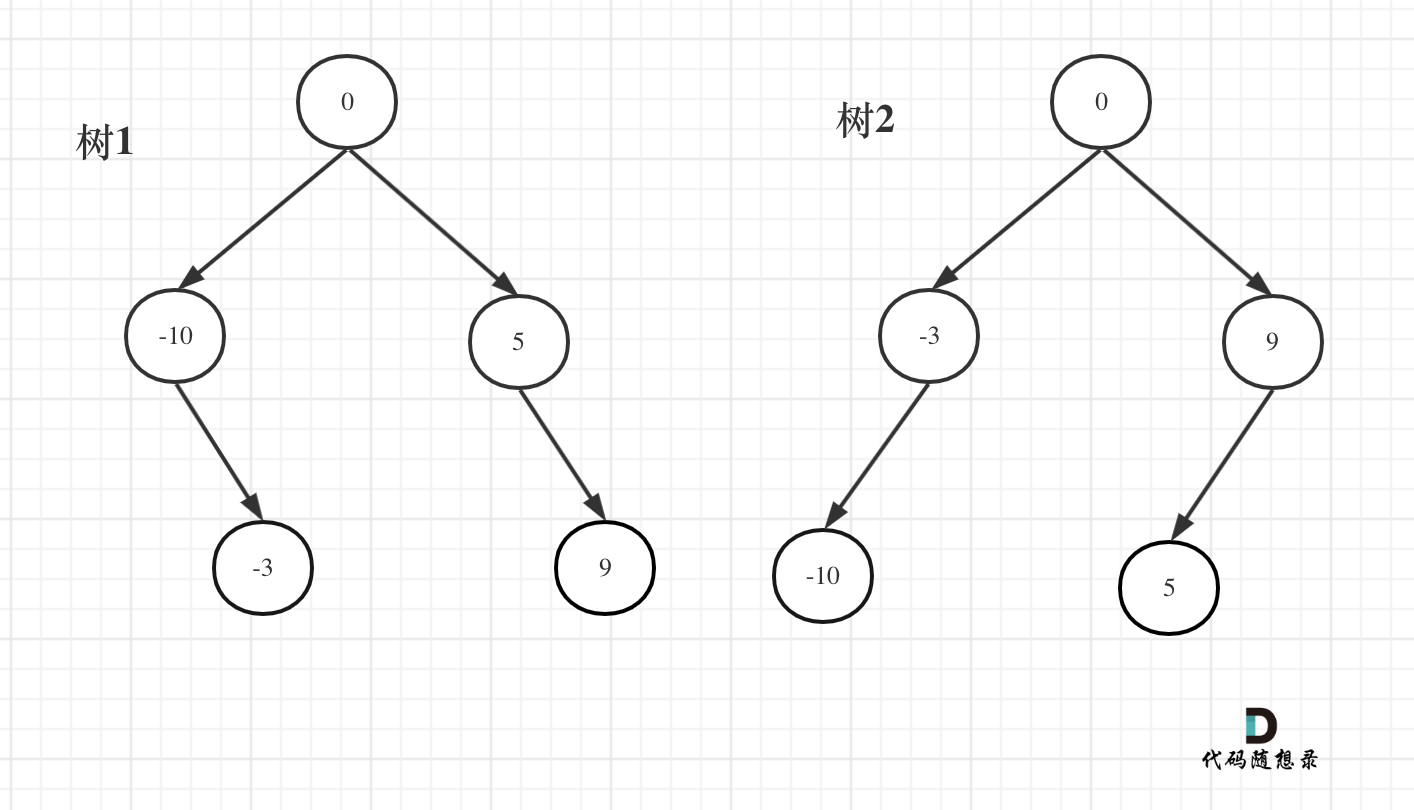
如果要分割的数组长度为偶数的时候,中间元素为两个,是取左边元素 就是树1,取右边元素就是树2。
// Solution类包含将已排序数组转换为二叉搜索树的方法
class Solution {
// 主方法,用于启动递归过程
public TreeNode sortedArrayToBST(int[] nums) {
// 调用辅助方法,传入数组和初始边界索引
return helper(nums, 0, nums.length - 1);
}
// 辅助递归方法,用于构建二叉搜索树
public TreeNode helper(int[] nums, int left, int right) {
// 如果左边界大于右边界,说明当前子数组为空,返回null
//注意这里传入的是左闭右闭的索引区间
if (left > right) {
return null;
}
// 计算中间索引,总是选择中间位置左边的数字作为根节点
int mid = (left + right) / 2;
// 创建一个新的树节点,值为数组中的中间值
TreeNode root = new TreeNode(nums[mid]);
// 递归构建左子树,左子树由中间值左边的部分数组构建
root.left = helper(nums, left, mid - 1);
// 递归构建右子树,右子树由中间值右边的部分数组构建
root.right = helper(nums, mid + 1, right);
// 返回构建好的子树的根节点
return root;
}
} 538.把二叉搜索树转换为累加树
538. 把二叉搜索树转换为累加树
中等
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
注意:本题和 1038: . - 力扣(LeetCode) 相同
示例 1:
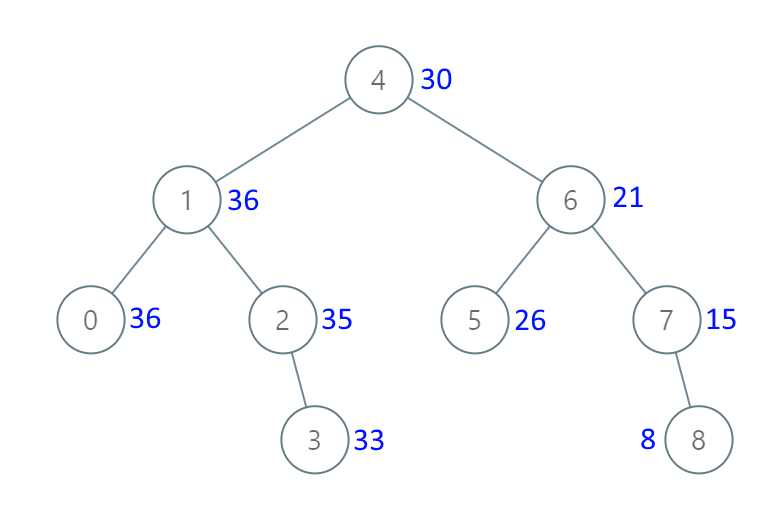
输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8] 输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2:
输入:root = [0,null,1] 输出:[1,null,1]
示例 3:
输入:root = [1,0,2] 输出:[3,3,2]
示例 4:
输入:root = [3,2,4,1] 输出:[7,9,4,10]
提示:
- 树中的节点数介于
0和104之间。 - 每个节点的值介于
-104和104之间。 - 树中的所有值 互不相同 。
- 给定的树为二叉搜索树。
累加树是使得每个节点的值是原来的节点值加上所有大于它的节点值之和。
通过右中左的访问方式,累加每个节点,然后通过sum更新
class Solution {
// 定义一个全局变量sum,用于累加节点值
int sum = 0;
// convertBST方法接受一个二叉搜索树的根节点作为参数
// 返回转换后的二叉搜索树的根节点
public TreeNode convertBST(TreeNode root) {
// 如果根节点为空,则直接返回null
if (root == null) {
return null;
}
// 先递归处理右子树
convertBST(root.right);
// 将当前节点的值累加到sum上
sum += root.val;
// 更新当前节点的值为sum,即从最大的节点到当前节点的所有节点值的总和
root.val = sum;
// 再递归处理左子树
convertBST(root.left);
// 返回转换后的根节点
return root;
}
}