前缀和思想其实就是一种简单的dp思想,也就是动态规划
什么时候用到前缀和?当要快速求出数组中某一个区间的和
前缀和模板
 暴力解法
暴力解法
定义一个指针从左向右遍历,并且累加值即可,这里就不过多赘述,主要还是来看前缀和
假设查找长度为n,要查q次,那时间复杂度就是O(n*q)
前缀和
我们可以定义一个与原数组相同大小的数组dp,dp[i]表示[1,i]区间内所有元素的和
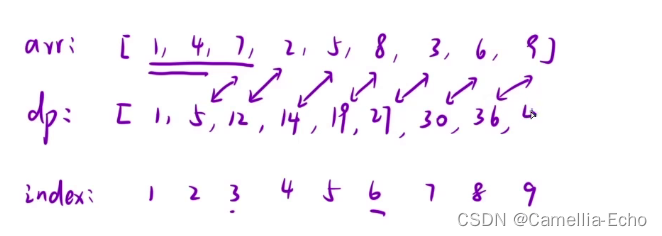
通过观察并结合dp[i]的第一可以发现规律:dp[i]=dp[i-1]+nums[i]——[1,i]区间的和等于[1,i-1]区间的和再加上nums[i]
当我们遍历完一边数组的时候,dp表也就完成了。当我们再去求[left,right]区间和的时候,发现要求的区间和等于dp[right]-dp[left-1](注意不是dp[left]),这一步的时间复杂度是O(1)的
所以时间复杂度由O(n*q)降为O(n)了
细节问题:为什么下标从1开始?
因为dp[i]=dp[i-1]+nums[i],如果从0开始就会出现-1,数组越界,不好处理,干脆从1开始方便
一维前缀和相关习题
和为K的子数组

解析
1.暴力解法
从第一个位置开始暴力枚举所有子数组——以i位置为起点的所有子数组,直到i等于size-1完成遍历
这里不过多赘述
2.前缀和
要知道和为k的子数组,肯定是要把所有数组的信息都收集到的,但是暴力枚举效率又太低了,所以要通过暴力枚举来优化
暴力枚举是遍历以i位置为起点的所有子数组,这里引入以i位置为结尾的所有子数组,这样往后遍历也是可以遍历所有子数组的
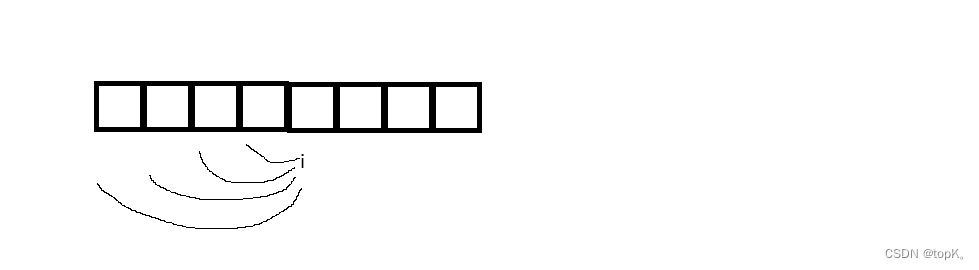
先定义前缀和数组dp,dp[i]表示[0,i]位置的子数组和,dp[i]=dp[i-1]+nums[i]
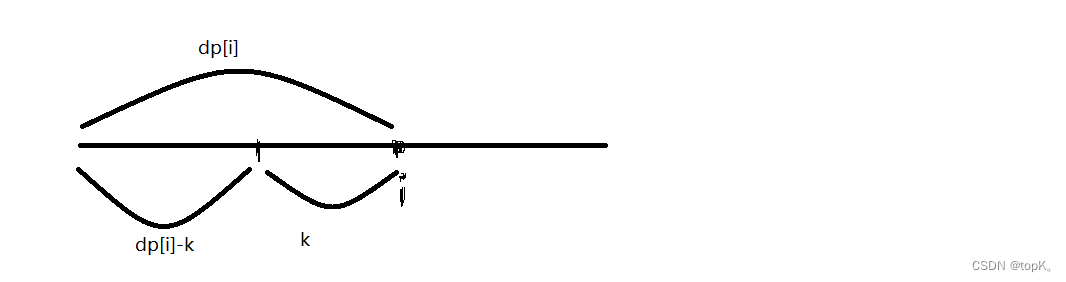
当遍历到i位置的时候,只关心dp[i]之前的子数组,目前我们知道dp[i],要求和为k的子数组
由上图可得问题可以转变成在[0,i-1]区间,有多少个前缀和等于dp[i]-k
这题如果只是建立和使用前缀和数组是远远不够的,假如你只使用前缀和数组,当cur在i位置的时候你要求有多少个前缀和等于dp[i]-k,那你还要定义一个变量prev=0,开始往后遍历到cur位置,仍然是O(N^2)的时间复杂度,还多了一次遍历数组的操作,这样还不如直接暴力枚举呢
上面的问题就是在创建前缀和数组的时候没有进行记录,所以这里要用哈希表对每个前缀和都进行记录,这样一次遍历完后就能直接获得结果
魔鬼小细节:
1.前缀和加入哈希表的时机
在计算i位置之前,哈希表里存的是[0,i-1]位置的前缀和
2.不用真正创建一个哈希表,因为这里可以发现i从左到右遍历,每个dp[i]只使用一次,因此使用一个sum表示dp[i]即可,当遍历的i+1的时候,sum+=nums[i+1]即可
3.如果整个数组的前缀和等于k呢?
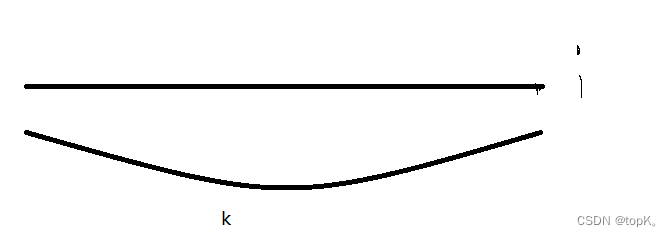
那么dp[i]-k==0,所以hash[0]要默认初始化为1
参考答案
class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
int n=nums.size(),ret=0,sum=0;
unordered_map<int,int> hash;
hash[0]=1;
for(auto x:nums)
{
sum+=x;
if(hash.count(sum-k))
{
ret+=hash[sum-k];
}
hash[sum]++;
}
return ret;
}
};由代码也可以看到如果出现整个数组的前缀和等于k的情况,ret是少加了一次hash[0]的情况的,所以hash[0]要默认初始化为1