【LetMeFly】1976.到达目的地的方案数：单源最短路的Dijkstra算法

力扣题目链接：https://leetcode.cn/problems/number-of-ways-to-arrive-at-destination/

你在一个城市里，城市由 n 个路口组成，路口编号为 0 到 n - 1 ，某些路口之间有 双向 道路。输入保证你可以从任意路口出发到达其他任意路口，且任意两个路口之间最多有一条路。

给你一个整数 n 和二维整数数组 roads ，其中 roads[i] = [ui, vi, timei] 表示在路口 ui 和 vi 之间有一条需要花费 timei 时间才能通过的道路。你想知道花费 最少时间 从路口 0 出发到达路口 n - 1 的方案数。

请返回花费 最少时间 到达目的地的 路径数目 。由于答案可能很大，将结果对 109 + 7 取余 后返回。

 

示例 1：

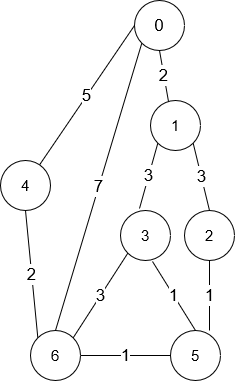
输入：n = 7, roads = [[0,6,7],[0,1,2],[1,2,3],[1,3,3],[6,3,3],[3,5,1],[6,5,1],[2,5,1],[0,4,5],[4,6,2]]
输出：4
解释：从路口 0 出发到路口 6 花费的最少时间是 7 分钟。
四条花费 7 分钟的路径分别为：
- 0 ➝ 6
- 0 ➝ 4 ➝ 6
- 0 ➝ 1 ➝ 2 ➝ 5 ➝ 6
- 0 ➝ 1 ➝ 3 ➝ 5 ➝ 6

示例 2：

输入：n = 2, roads = [[1,0,10]]
输出：1
解释：只有一条从路口 0 到路口 1 的路，花费 10 分钟。

 

提示：

• 1 <= n <= 200
• n - 1 <= roads.length <= n * (n - 1) / 2
• roads[i].length == 3
• 0 <= ui, vi <= n - 1
• 1 <= timei <= 109
• ui != vi
• 任意两个路口之间至多有一条路。
• 从任意路口出发，你能够到达其他任意路口。

方法一：单源最短路的Dijkstra算法

“单源最短路”意思是从一个点出发到其他点的最短路径。单源最短路的Dijkstra算法也可以看我之前做的视频。

总之Dijkstra算法就是，我们从起点开始:

计算所有能一步到达的点中，哪个点距离起点最近。

下一步就走到这个点，然后能一步到达的点就更新了。

直到走完所有的点为止。

对于这道题，我们在“往前走”的同时，记录一下走到这一步的“方案数”：

• 若从当前点走到点a的距离 小于 a原本到起点的距离，则说明发现了新大“路”（更近的路）。舍弃掉之前的方案数，将点a的方案数变为当前点的方案数，并更新最短距离，可以从点a开始往深处继续探索。
• 若从当前点走到点a的距离 等于 a原本到起点的距离，则说明又发现了一条同为最近路的路。将点a的方案数加上当前点的方案数。
• 否则，已有更短路，不做考虑。

最终返回终点的路径数即为答案。

• 时间复杂度$O(m\log m)$
• 空间复杂度$O(n+m)$

AC代码

C++

typedef long long ll;
const ll MOD = 1e9 + 7;

class Solution {
public:
    int countPaths(int n, vector<vector<int>>& roads) {
        vector<vector<pair<int, int>>> graph(n);
        for (vector<int>& road : roads) {
            graph[road[0]].push_back({road[1], road[2]});
            graph[road[1]].push_back({road[0], road[2]});
        }
        vector<ll> way(n);
        way[0] = 1;
        vector<ll> dis(n, 1e18);
        dis[0] = 0;
        priority_queue<pair<ll, int>, vector<pair<ll, int>>, greater<pair<ll, int>>> pq;
        pq.push({0, 0});
        while (pq.size()) {
            auto [thisDistance, thisNode] = pq.top();
            pq.pop();
            if (thisDistance > dis[thisNode]) {  // 有更优解了
                continue;
            }
            for (auto [nextNode, nextDistance] : graph[thisNode]) {
                if (thisDistance + nextDistance < dis[nextNode]) {
                    dis[nextNode] = thisDistance + nextDistance;
                    way[nextNode] = way[thisNode];
                    pq.push({dis[nextNode], nextNode});
                }
                else if (thisDistance + nextDistance == dis[nextNode]) {
                    way[nextNode] = (way[nextNode] + way[thisNode]) % MOD;
                }
            }
        }
        return way.back();
    }
};

Python

# from typing import List
# import heapq

MOD = int(1e9) + 7

class Solution:
    def countPaths(self, n: int, roads: List[List[int]]) -> int:
        graph = [[] for _ in range(n)]
        for x, y, d in roads:
            graph[x].append((y, d))
            graph[y].append((x, d))
        way = [0] * n
        way[0] = 1
        dis = [int(1e18)] * n
        dis[0] = 0
        pq = [(0, 0)]
        while pq:
            thisDistance, thisNode = heapq.heappop(pq)
            if thisDistance > dis[thisNode]:
                continue
            for nextNode, nextDistance in graph[thisNode]:
                if nextDistance + thisDistance < dis[nextNode]:
                    dis[nextNode] = nextDistance + thisDistance
                    way[nextNode] = way[thisNode]
                    heapq.heappush(pq, (dis[nextNode], nextNode))
                elif nextDistance + thisDistance == dis[nextNode]:
                    way[nextNode] = (way[nextNode] + way[thisNode]) % MOD
        return way[-1]

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/136481215