一、张量概念
张量(tensor)是一个多维数组,它是向量(一维数组)和矩阵(二维数组)的推广。在数学和物理学中,张量是一种广泛应用的概念,用来描述物理量在空间中的分布和变化。
二、张量分类
张量可以根据它们变换时的性质进行分类,常见的分类包括:
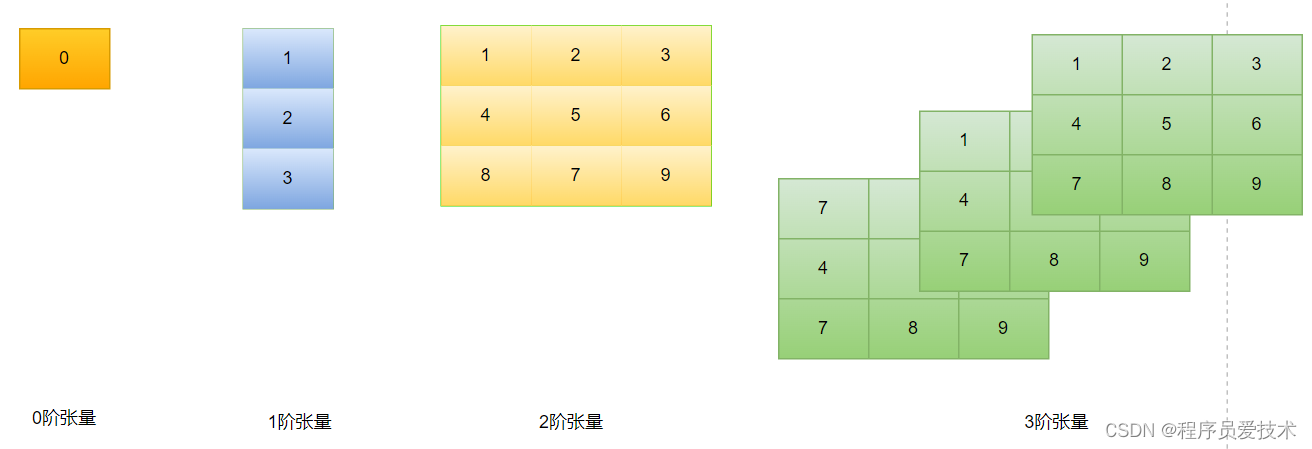
- 根据阶数:零阶张量是标量,一阶张量是向量,二阶张量是矩阵,三阶及以上的张量称为高阶张量。
- 根据变换性质:协变张量和逆变张量,在坐标变换下有不同的变换规律。
- 根据对称性:对称张量和反对称张量,具有不同的对称性质。
张量在物理学、工程学、计算机科学等领域都有广泛的应用,比如在机器学习和深度学习中,神经网络的参数和数据通常以张量的形式表示和处理。张量在数值计算、图像处理、自然语言处理等领域都扮演着重要的角色。
在实际使用中,张量可以通过各种数学运算来处理和操作,比如加法、乘法、转置、求导等操作。通过这些操作,可以实现对张量的组合、变换和分析,从而解决实际问题。
三、快速理解张量
要快速理解张量,可以通过以下几个步骤来进行:
-
从基础开始理解:首先,从一维数组(向量)和二维数组(矩阵)开始,理解它们分别是零阶张量和一阶张量的特例。这有助于建立起对张量的概念基础。
-
理解张量的几何意义:将张量看作是描述物理量在空间中分布和变化的工具。想象不同阶数的张量在空间中的表现形式,可以帮助理解张量的几何意义。
-
学习张量的表示和操作:了解如何表示不同阶数的张量,以及如何进行张量的加法、乘法、转置等基本操作。这有助于理解张量的运算规则和性质。
-
掌握张量的应用领域:学习张量在不同领域的应用,比如物理学、工程学、计算机科学等。通过实际应用案例,可以更好地理解张量的重要性和作用。
-
练习和实践:通过练习张量的相关问题和实际应用,逐渐加深对张量的理解。可以尝试使用编程工具如Python中的NumPy或PyTorch库来操作张量,加深对张量的认识。
总的来说,理解张量需要一个渐进的过程,结合理论和实践,逐步加深对张量概念的理解和运用。