有限域GF(2^8)上的乘法运算可以看成多项式的乘法

5e转换成二进制为0101 1110，对应的多项式为x^6+x^4+x^3+x^2+x

3f转换成二进制为0011 1111，对应的多项式为x^5+x^4+x^3+x^2+x+1

将这两个多项式相乘再模多项式x^8+x^4+x^3+x+1得到结果为1110 0101，转换为十六进制为e5

代码实现

def gf256_multiply(a_hex, b_hex):
    a = int(a_hex, 16)  # 将十六进制字符串转换为整数
    b = int(b_hex, 16)

    result = 0
    while a > 0 and b > 0:
        if b & 1:  # 如果b的最低位为1
            result ^= a  # 则将a与结果异或
        a <<= 1  # 将a左移一位
        if a & 0x100:  # 如果a的最高位为1
            a ^= 0x11B  # GF(2^8)上的不可约多项式 1

        b >>= 1  # 将b右移一位

    return hex(result)[2:]  # 将结果转换为十六进制字符串，去掉前缀'0x'


# 输入两个GF(2^8)上的十六进制元素
a_hex = input("请输入GF(2^8)上的十六进制元素 a：")
b_hex = input("请输入GF(2^8)上的十六进制元素 b：")

result_hex = gf256_multiply(a_hex, b_hex)
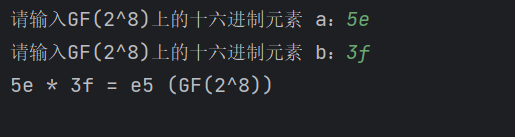
print(f"{a_hex} * {b_hex} = {result_hex} (GF(2^8))")

运行结果