---

前言

回溯法就是暴力搜索，并不是什么高效的算法，最多再剪枝一下。

组合问题：N个数里面按一定规则找出k个数的集合
排列问题：N个数按一定规则全排列，有几种排列方式
切割问题：一个字符串按一定规则有几种切割方式
子集问题：一个N个数的集合里有多少符合条件的子集
棋盘问题：N皇后，解数独等等

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、组合问题

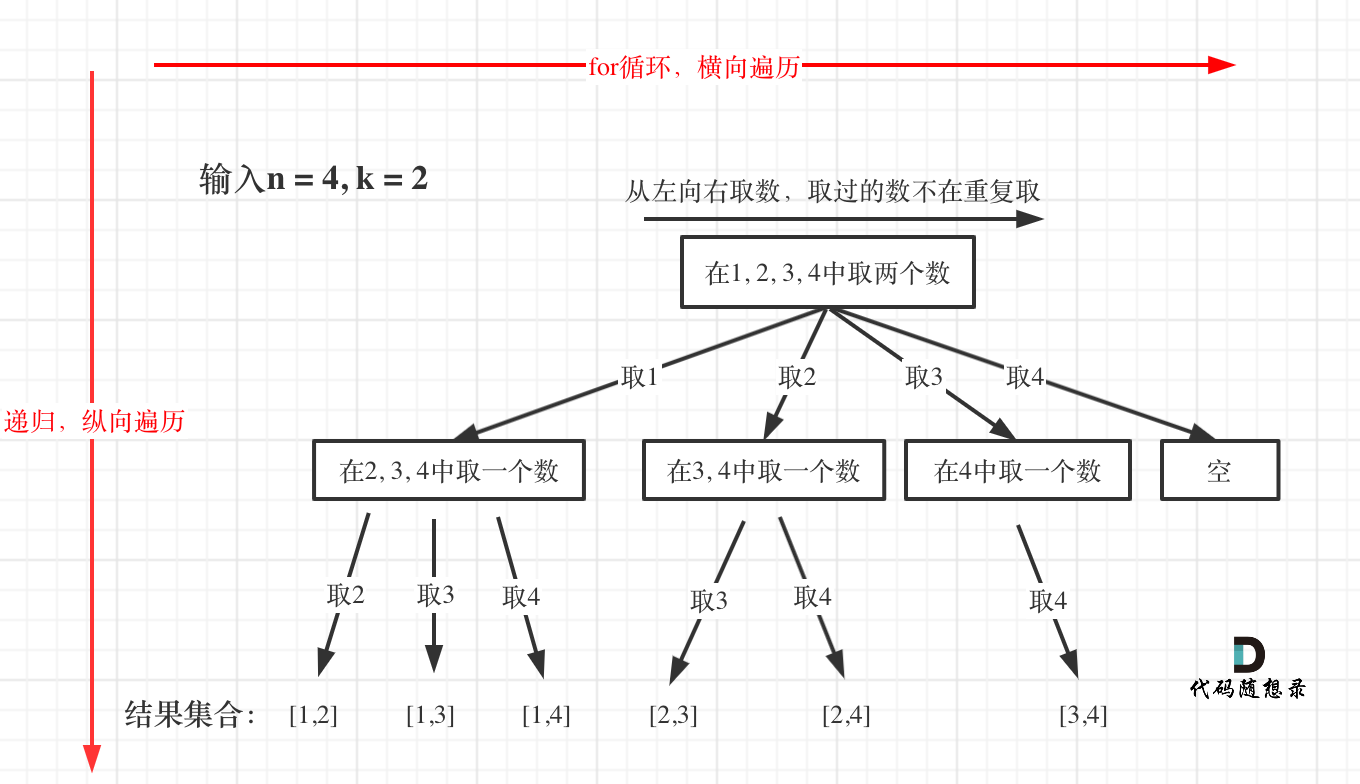
给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按任意顺序返回答案。

示例

• 输入：n = 4, k = 2
• 输出：
  [
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
  ]

通过for循环横向遍历，递归纵向遍历，回溯不断调整结果集

对于组合问题，什么时候需要startIndex，也需要考虑
如果是一个集合来求组合的话，就需要startIndex 216.组合总和III 、第77题. 组合
如果是多个集合求组和，各集合互相不影响，就不要startIndex17.电话号码的字母组合

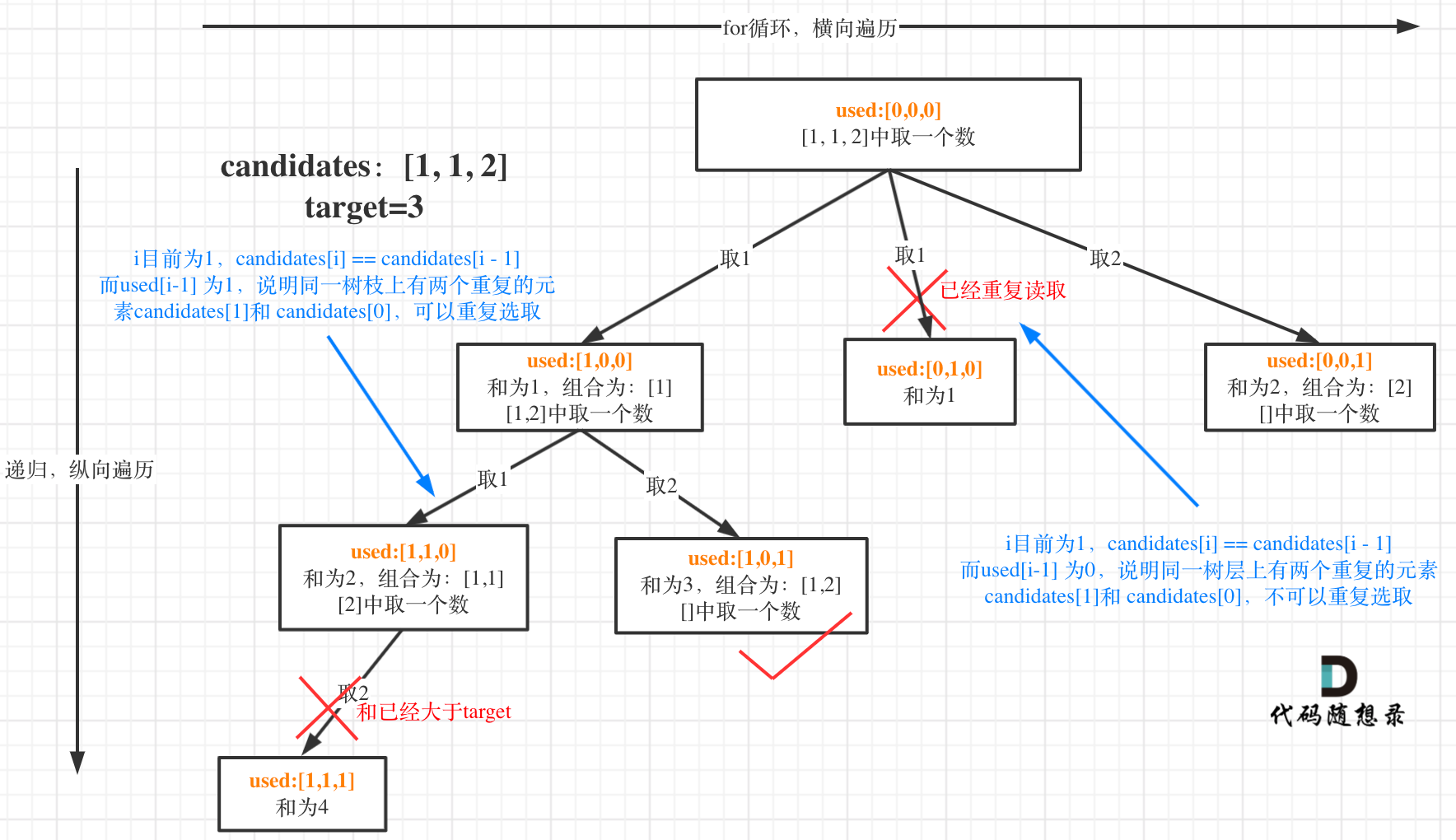
去重问题，树枝去重和树层去重，这里使用了used容器记录遍历情况。
used[i - 1] == true，说明同一树枝该相同元素被使用过
used[i - 1] == false，说明同一树层该相同袁术被使用过

二、切割问题

有如下几个难点：

• 如何模拟切割线
• 切割问题中递归如何终止
• 在递归循环中如何截取子串
• 如何判断回文

131.分割回文串
递归用来纵向遍历，for循环用来横向遍历，切割线（就是图中的红线）切割到字符串的结尾位置，说明找到了一个切割方法。

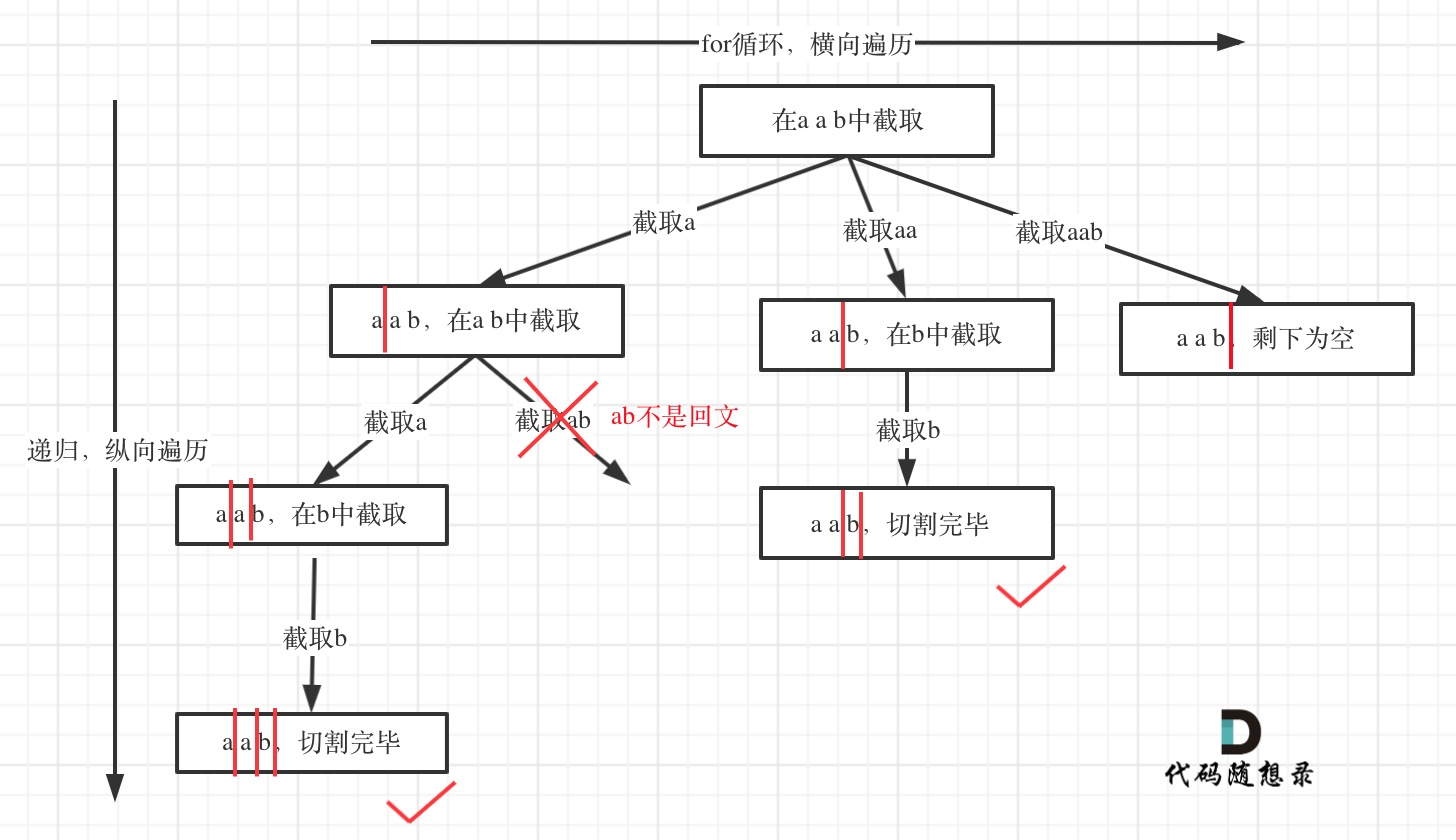
截取字符串
在for (int i = startIndex; i < s.size(); i++)循环中，我们 定义了起始位置startIndex，那么 [startIndex, i] 就是要截取的子串。

for (int i = startIndex; i < s.size(); i++) {
    if (isPalindrome(s, startIndex, i)) { // 是回文子串
        // 获取[startIndex,i]在s中的子串
        string str = s.substr(startIndex, i - startIndex + 1);
        path.push_back(str);
    } else {                // 如果不是则直接跳过
        continue;
    }
    backtracking(s, i + 1); // 寻找i+1为起始位置的子串
    path.pop_back();        // 回溯过程，弹出本次已经添加的子串
}

---

三、子集问题

在树形结构中子集问题是要收集所有节点的结果，而组合问题是收集叶子节点的结果。

四、排列问题

排列是有序的，也就是说 [1,2] 和 [2,1] 是两个集合，这和之前分析的子集以及组合所不同的地方。所以处理排列问题就不用使用startIndex了。

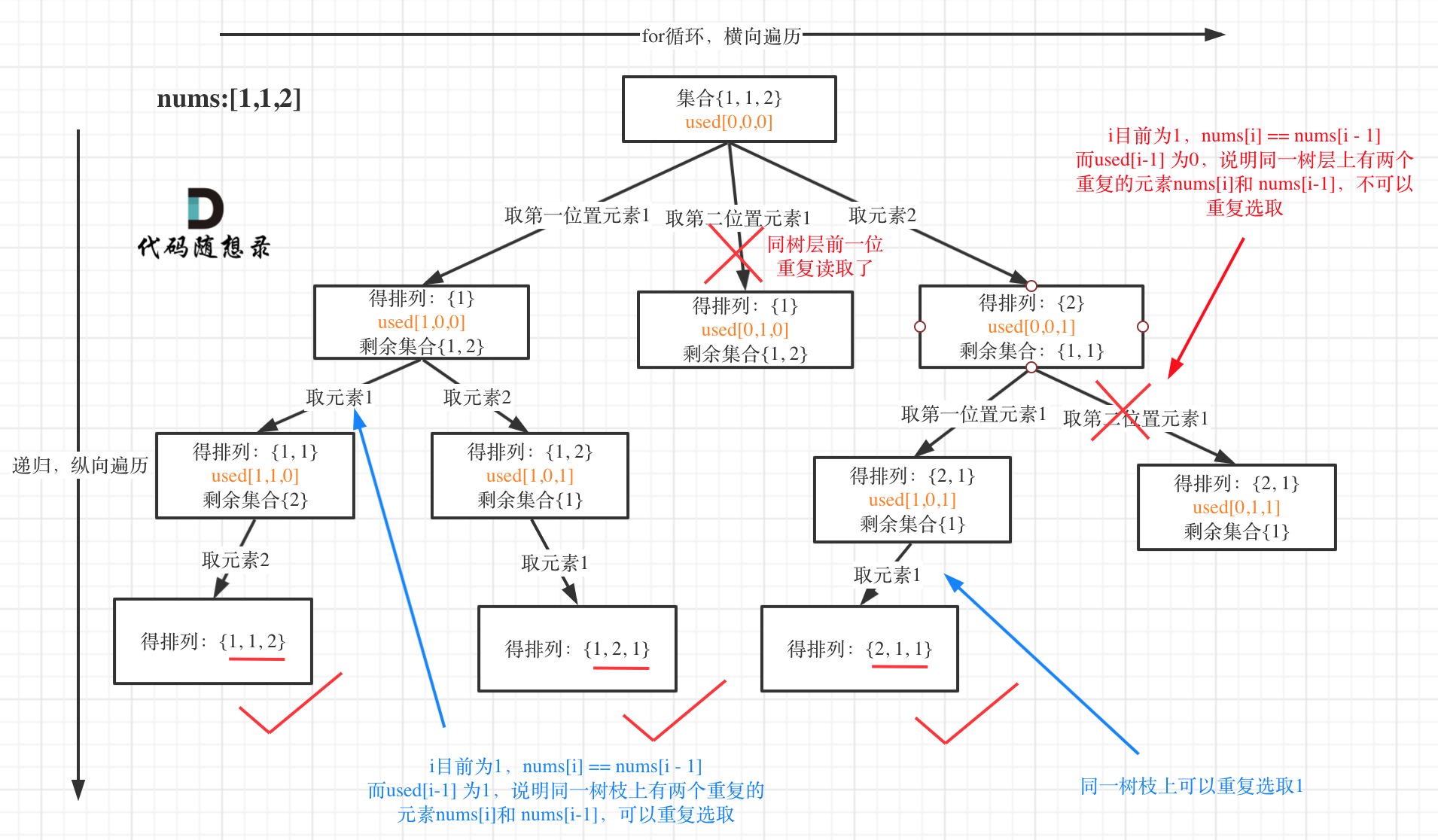
所以我们使用used去重，排列树层上去重(used[i - 1] == false)，树枝上去重（used[i - 1] == true）

五、性能分析

子集问题分析：

• 时间复杂度：O(2^{n)，因为每一个元素的状态无外乎取与不取，所以时间复杂度为O(2}n)。
• 空间复杂度：O(n)，递归深度为n，所以系统栈所用空间为O(n)。每一层递归所用的空间都是常数级别。注意代码里的result和path都是全局变量，就算是放在参数里，传的也是引用，并不会新申请内存空间，最终空间复杂度为O(n)。

排列问题分析：

• 时间复杂度：O(n!)，这个可以从排列的树形图中很明显发现，每一层节点为n，第二层每一个分支都延伸了n-1个分支，再往下又是n-2个分支，所以一直到叶子节点一共就是 n * (n-1) * (n-2) * … * 1 = n!。
• 空间复杂度：O(n)，和子集问题同理。

组合问题分析：

• 时间复杂度：O(2^n)，组合问题其实就是一种子集的问题，所以组合问题最坏的情况，也不会超过子集问题的时间复杂度。
• 空间复杂度：O(n)，和子集问题同理。

N皇后问题分析：

• 时间复杂度：O(n!)，其实如果看树形图的话，直觉上是O(n^n)，但皇后之间不能见面所以在搜索的过程中是有剪枝的，最差也就是O(n!)，n!表示n * (n-1) * … * 1。
• 空间复杂度：O(n)，和子集问题同理。