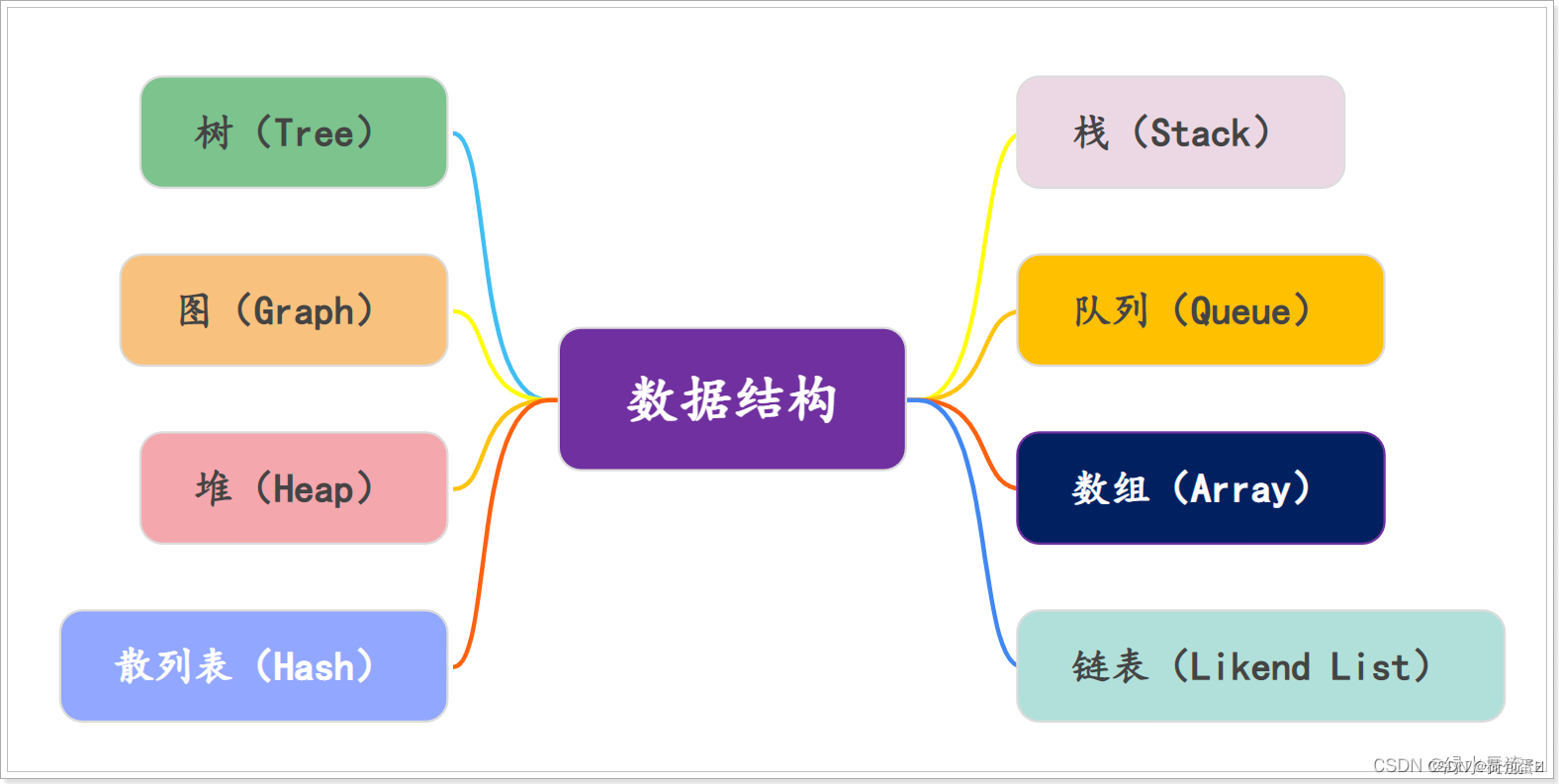
一、线性结构:数组、链表、哈希表;队列、栈
1.数组:
数组是有序元素的序列,在内存中的分配是连续的,数组会为存储的元素都分配一个下标(索引),此下标是一个自增连续的,访问数组中的元素通过下标进行访问;数组下标从0开始访问;
2.链表:
链表是由一系列节点Node(也可称元素)组成,数据元素的逻辑顺序是通过链表的指针地址实现,通常情况下,每个节点包含两个部分,一个用于存储元素的内存地址,名叫数据域,另一个则指向下一个相邻节点地址的指针,名叫指针域;根据链表的指向不同可分为单向链表、双向链表、循环链表等;我们本章介绍的是单向链表,也是所有链表中最常见、最简单的链表;
3.散列表(哈希表):
也叫哈希表,是根据键和值 (key和value) 直接进行访问的数据结构,通过key和value来映射到集合中的一个位置,这样就可以很快找到集合中的对应元素。它利用数组支持按照下标访问的特性,所以散列表其实是数组的一种扩展,由数组演化而来。
散列表首先需要根据key来计算数据存储的位置,也就是数组索引的下标;
HashValue=hash(key)
散列表就是把Key通过一个固定的算法函数既所谓的哈希函数转换成一个整型数字,然后就将该数字对数组长度进行取余,取余结果就当作数组的下标,将value存储在以该数字为下标的数组空间里,这种存储空间可以充分利用数组的查找优势来查找元素,所以查找的速度很快
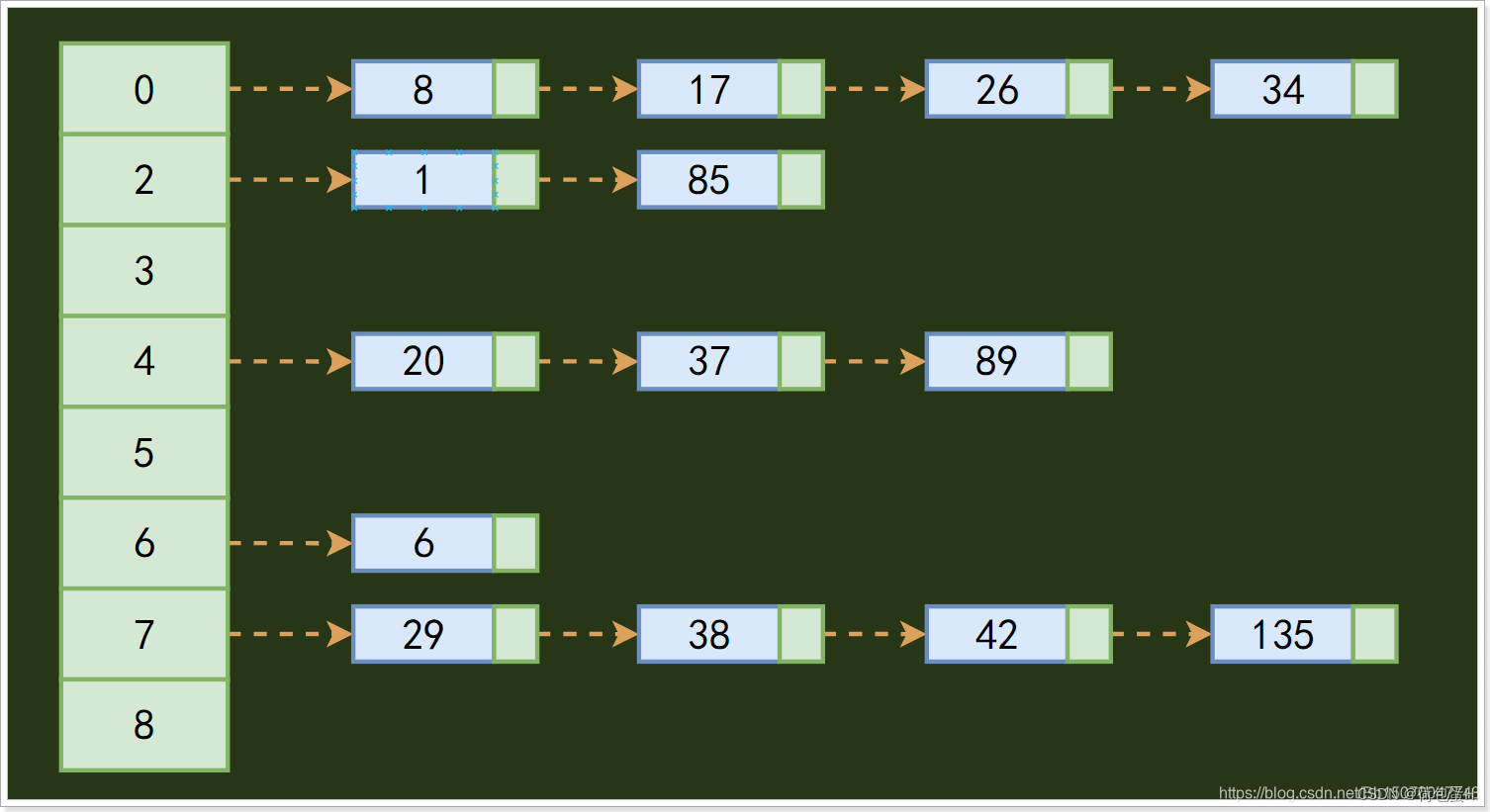
在散列表中,左边是个数组,数组的每个成员包括一个指针,指向一个链表的头,当然这个链表可能为空,也可能元素很多。我们根据元素的一些特征把元素分配到不同的链表中去,也是根据这些特征,找到正确的链表,再从链表中找出这个元素。
4.队列:
队列与栈一样,也是一种线性表,其限制是仅允许在表的一端进行插入,而在表的另一端进行删除。队列的特点是先进先出,从一端放入元素的操作称为入队,取出元素为出队;(先进先出 )

5.栈:
是一种特殊的线性表,仅能在线性表的一端操作,栈顶允许操作,栈底不允许操作。 栈的特点是:先进后出从栈顶放入元素的操作叫入栈(压栈),取出元素叫出栈(弹栈)
入栈操作:
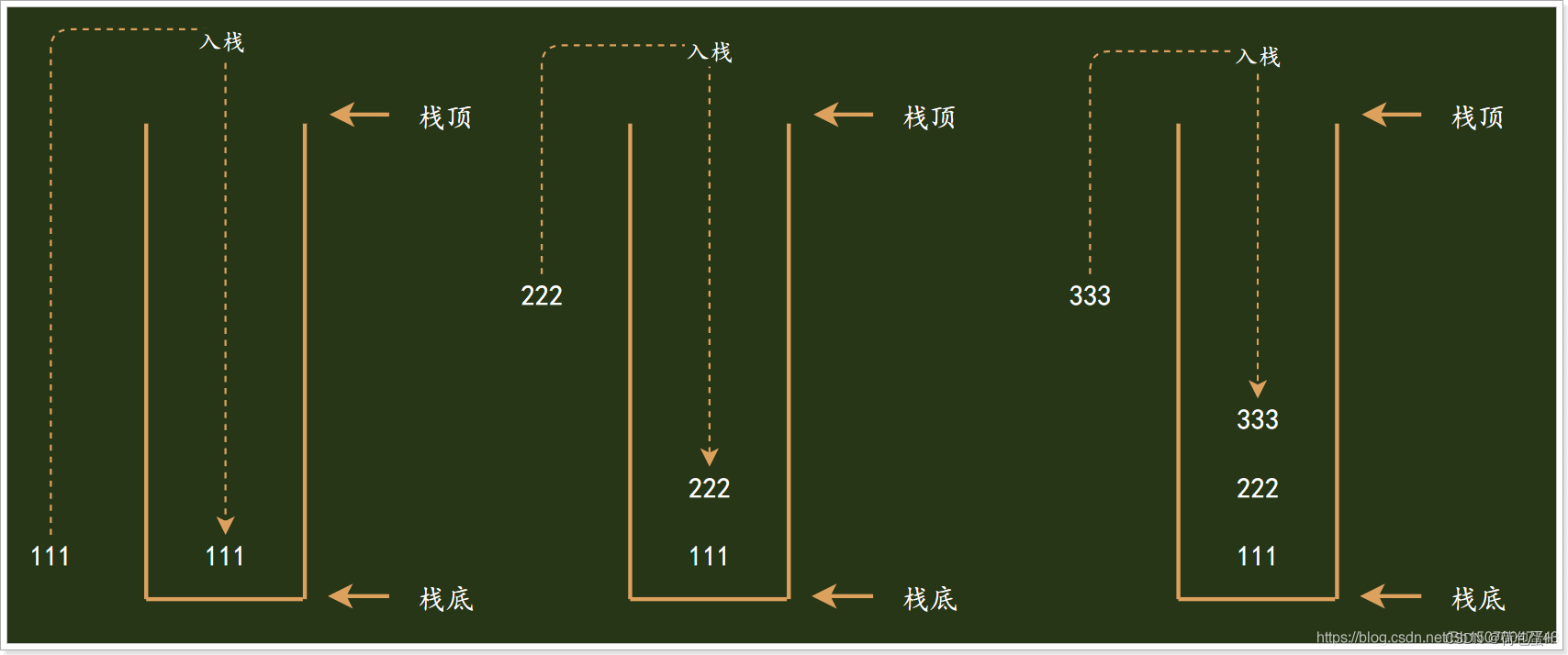
出栈操作:
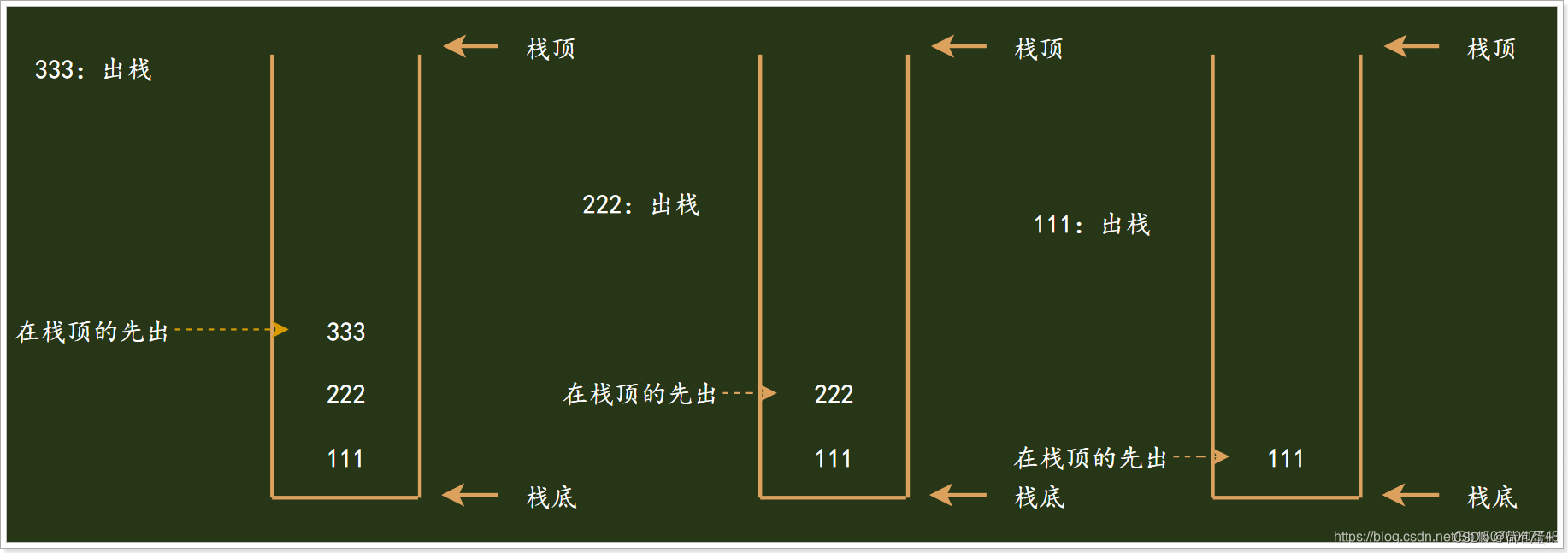
| 数据结构 | 优点 | 缺点 |
|---|---|---|
| 数组 | 查找快 | 增删慢 |
| 链表 | 增删快 | 查找慢 |
| 哈希表 | 增删、查找都快 | 数据散列,对存储空间有浪费 |
| 栈 | 顶部元素插入和取出快 | 除顶部元素外,存取其他元素都很慢 |
| 队列 | 顶部元素取出和尾部元素插入快 | 存取其他元素都很慢 |
| 二叉树 | 增删、查找都快 | 删除算法复杂 |
| 红黑树 | 增删、查找都快 | 算法复杂 |
| 位图 | 节省存储空间 | 不方便描述复杂的数据关系 |
二、非线性结构有:堆、树(二叉树、B树、B+树
6.堆:
堆可以看做是一颗用数组实现的二叉树,所以它没有使用父指针或者子指针。堆根据“堆属性”来排序,“堆属性”决定了树中节点的位置。
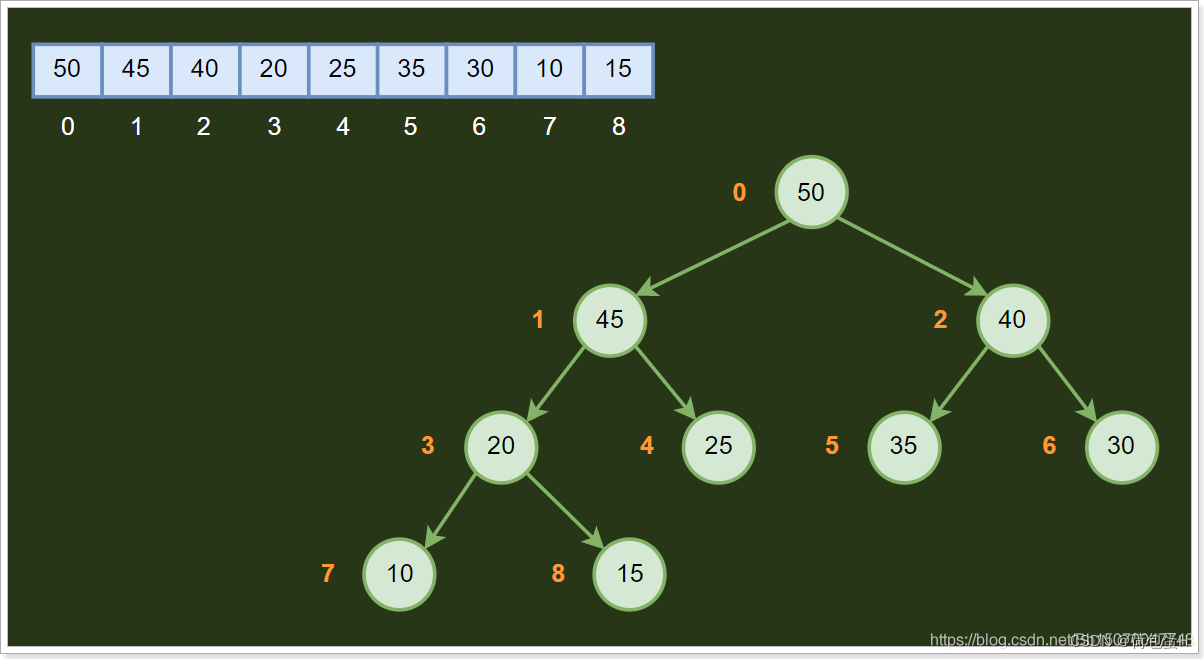
堆的特性:如果一个结点的位置为k,则它的父结点的位置为[k/2],而它的两个子结点的位置则分别为2k和2k+1。这样,在不使用指针的情况下,我们也可以通过计算数组的索引在树中上下移动:从arr[k]向上一层,就令k等于k/2,向下一层就令k等于2k或2k+1。
堆的定义如下:n个元素的序列{k1,k2,ki,…,kn}当且仅当满足下关系时,称之为堆;
(ki <= k2i,ki <= k2i+1)或者(ki >= k2i,ki >= k2i+1)满足前者的表达式的成为小顶堆(小根堆),满足后者表达式的为大顶堆(大根堆),很明显我们上面画的堆数据结构是一个大根堆;
大小根堆数据结构图:
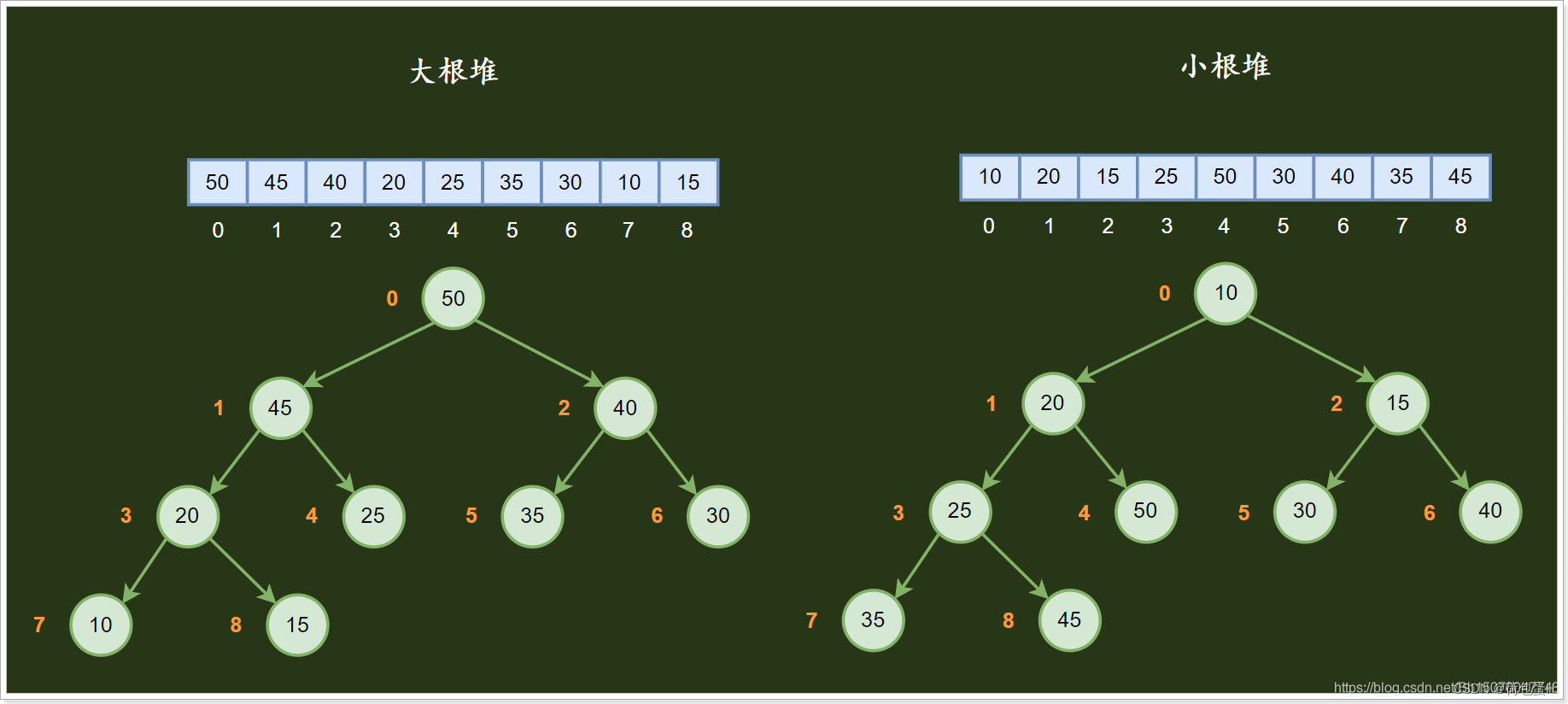
一般来说将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。常见的堆有二叉堆、斐波那契堆等。
7.树:
它是由n(n>=1)个有限节点组成一个具有层次关系的集合。把它叫做 “树” 是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
1)每个节点有0个或多个子节点;
2)没有父节点的节点称为根节点;
3)每一个非根节点有且只有一个父节点;
4)除了根节点外,每个子节点可以分为多个不相交的子树;
5)右子树永远比左子树大,读取顺序从左到右;
树的分类有非常多种,平衡二叉树(AVL)、红黑树RBL(R-B Tree)、B树(B-Tree)、B+树(B+Tree)等,但最早都是由二叉树演变过去的;
1.二叉树分类
每个结点最多有两颗子树
时间复杂度最好情况是O(logn) ,最坏情况下时间复杂度O(n)
1)满二叉树:如果一个二叉树的层数为K,且结点总数是(2^k) -1 ,则它就是满二叉树。
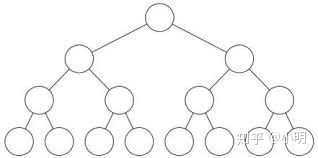
2)完全二叉树:如果一个二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
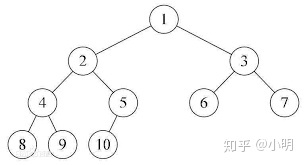
3)二叉查找树:左子树上的值都比其根节点小,右子树上的值都比其根节点大。
二叉查找树的中序遍历一定是从小到大排序的。
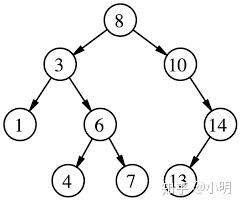
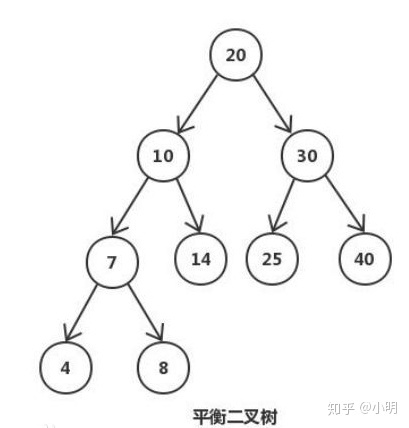
4)平衡二叉树(红黑树):是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
平衡二叉树必须是二叉查找树
性能:平衡二叉树在添加和删除时需要进行复杂的旋转保持整个树的平衡,最终,插入、查找的时间复杂度都是 O(logn),性能已经相当好了。
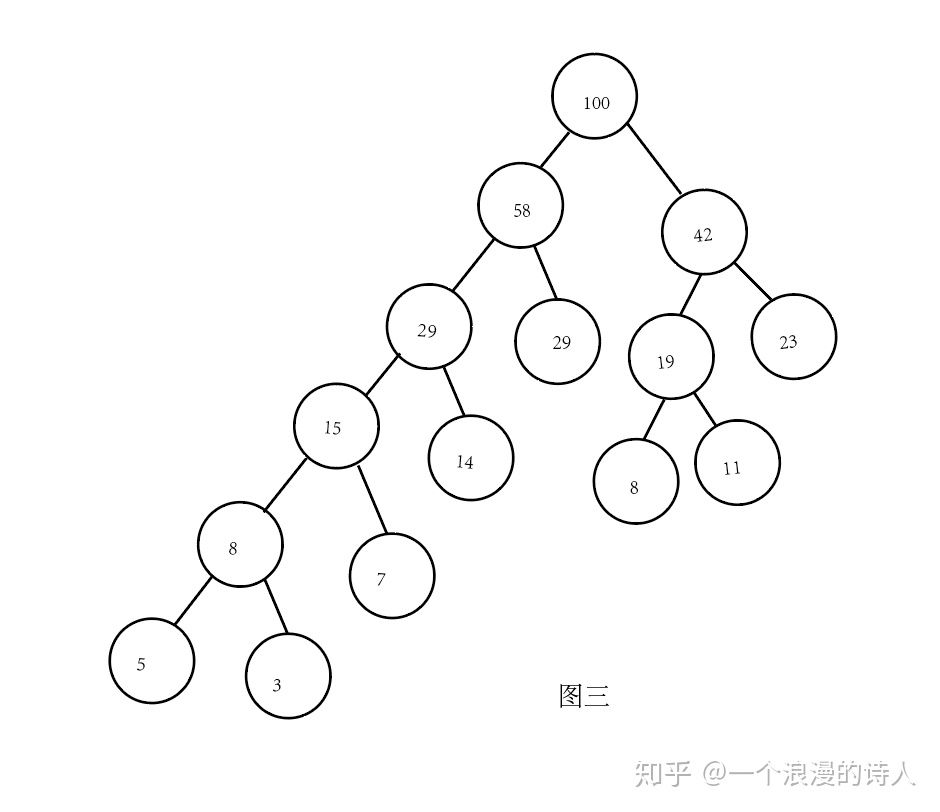
5)最优二叉树(哈夫曼树): 树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。
哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。应用:哈夫曼编码。
2.红黑树:是一种自平衡二叉查找树。应用内存排序。
插入和删除的最坏的时间复杂度是O(log N) 。
红黑树左旋和右旋的目的是为了自平衡。
参考:1.红黑树、B+树 2.红黑树在什么时候左旋 右旋 如何旋转
1)每个节点非红即黑;
2)根节点是黑的;
3)每个叶节点(叶节点即树尾端NULL指针或NULL节点)都是黑的;
4)如果一个节点是红的,那么它的两儿子都是黑的;
5)对于任意节点而言,其到叶子点树NULL指针的每条路径都包含相同数目的黑节点;
6)高度始终保持在h = logn
7)红黑树的查找、插入、删除的时间复杂度最坏为O(log n)
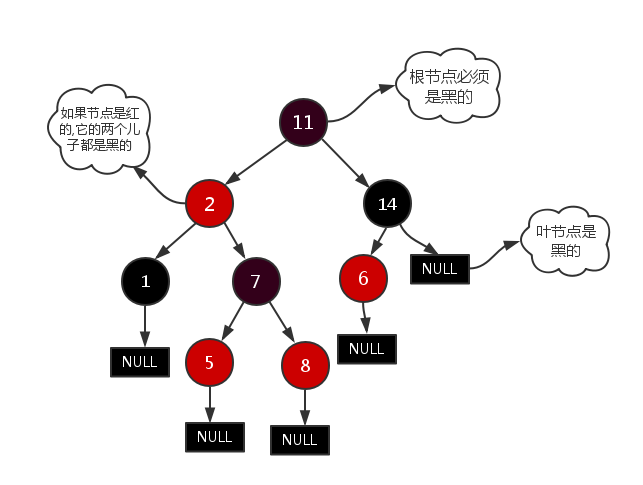
2.1 变色规则 红黑树使用红黑二色进行“着色”,目的是利用颜色值作为二叉树的平衡对称性的检查。
当前结点的父亲是红色,且它的祖父结点的另一个子结点也是红色(叔叔结点):
(1)把父节点设为黑色
(2)把叔叔也设为黑色
(3)把祖父也就是父亲的父亲设为红色(爷爷)
(4)把指针定义到祖父结点设为当前要操作的(爷爷)分析的点变换的规则
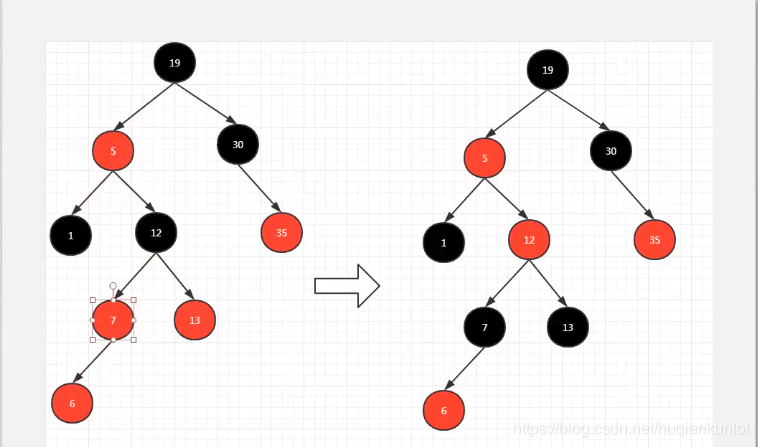
这里我们新插入一个值 6 ( 插入的节点都是红色的 所以 6 是红色的节点 ) ,变色后的图形。
红黑树的创建:节点的初始颜色为红色。
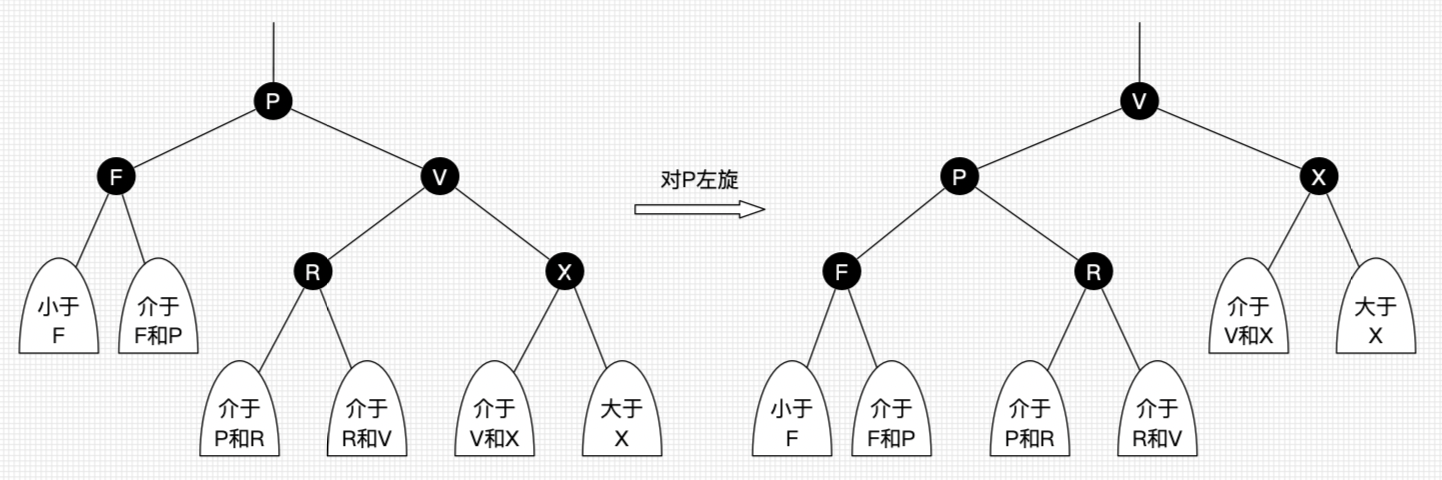
2.2 左旋:
以某个结点作为支点(旋转结点),其右子结点变为旋转结点的父结点,右子结点的左子结点变为旋转结点的右子结点,左子结点保持不变。
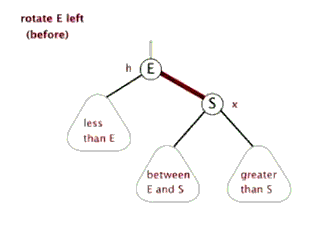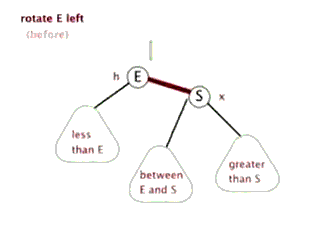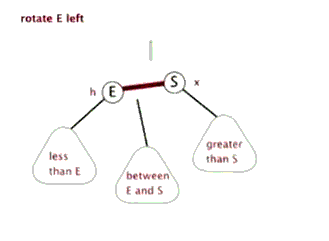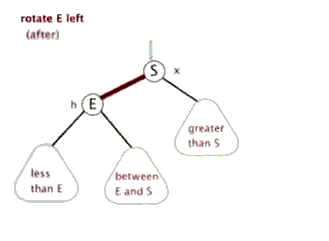
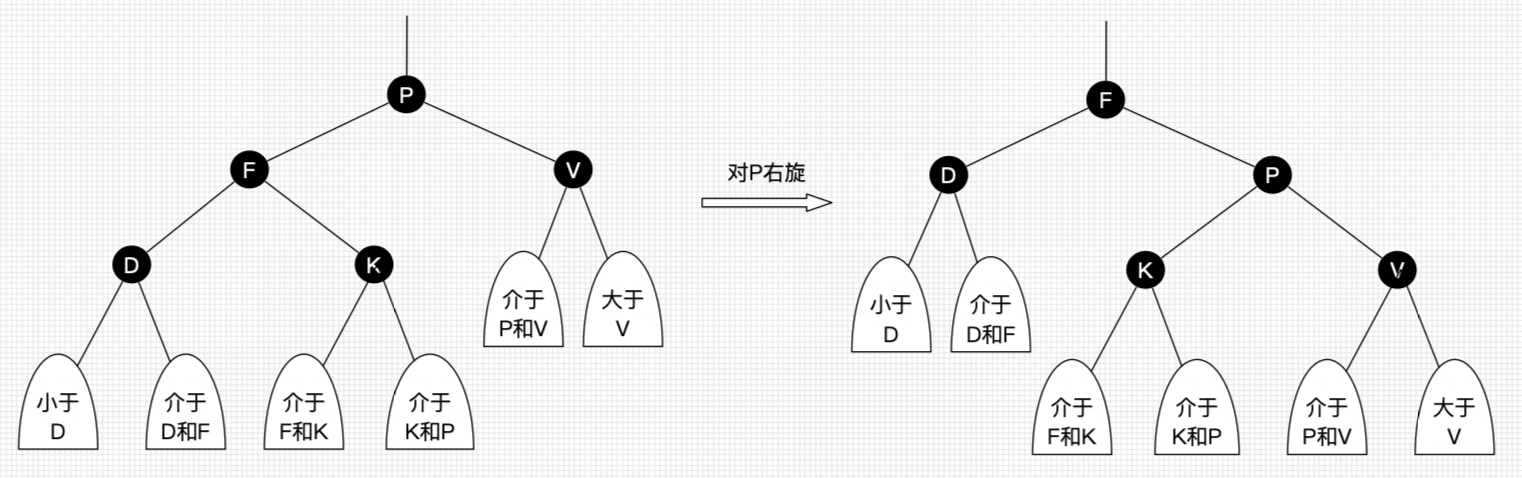
2.3 右旋:
以某个结点作为支点(旋转结点),其左子结点变为旋转结点的父结点,左子结点的右子结点变为旋转结点的左子结点,右子结点保持不变。
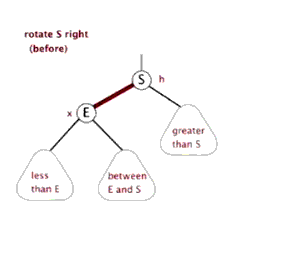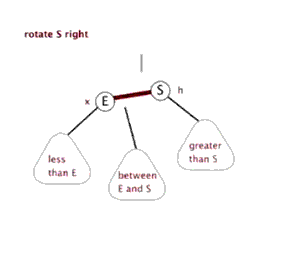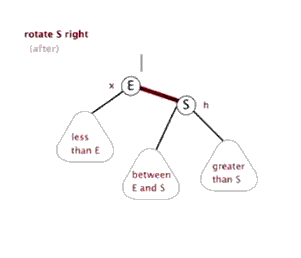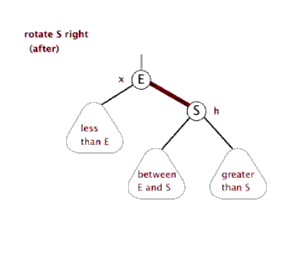
2.4 红黑树查找:和二叉平衡树的查找一样
3.B树(多叉树):
平衡多路查找树(查找路径不只两个),不同于常见的二叉树,它是一种多叉树。O(logN)
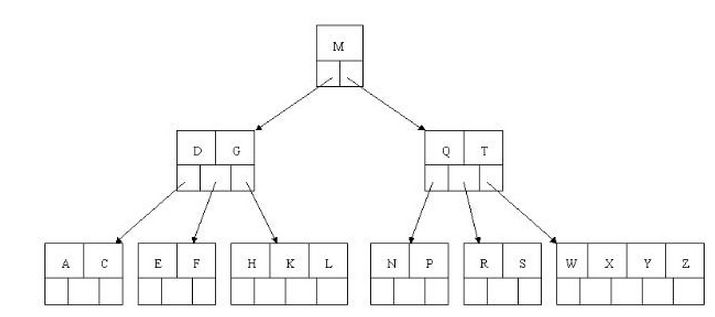
4.B+树:
是一种自平衡树数据结构,它保持数据排序;在进行搜索、顺序访问、插入和删除的复杂度是O(log n)且B+树只在叶子节点中存放数据,所以消除了一些B树的缺陷。非叶子节点只保存索引,不保存实际的数据,数据都保存在叶子节点中。O(nlogn)
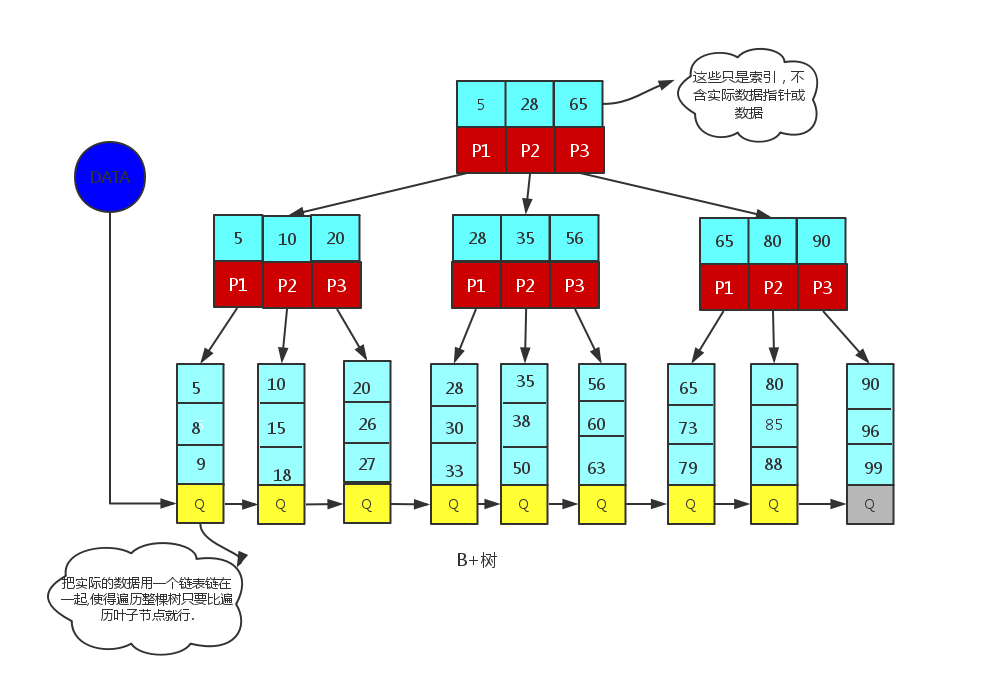
4.1 B+树查找:树的高度低,支持范围查找
4.2 mysql为什么采用B+树
1)磁盘IO的次数更少
2)支持范围查找
4.3 B树与B+树的区别
1)B+树所有数据都存在叶子节点
2)B+树的叶子节点有双向指针,方便范围查找,且叶节点上的数据从小到大顺序连接
三、图(对现实世界建模)
图是一系列顶点(元素)的集合,这些顶点通过一系列边连接起来组成图这种数据结构。顶点用圆圈表示,边就是这些圆圈之间的连线。顶点之间通过边连接。
图分为有向图和无向图:
有向图:边不仅连接两个顶点,并且具有方向;
无向图:边仅仅连接两个顶点,没有其他含义;
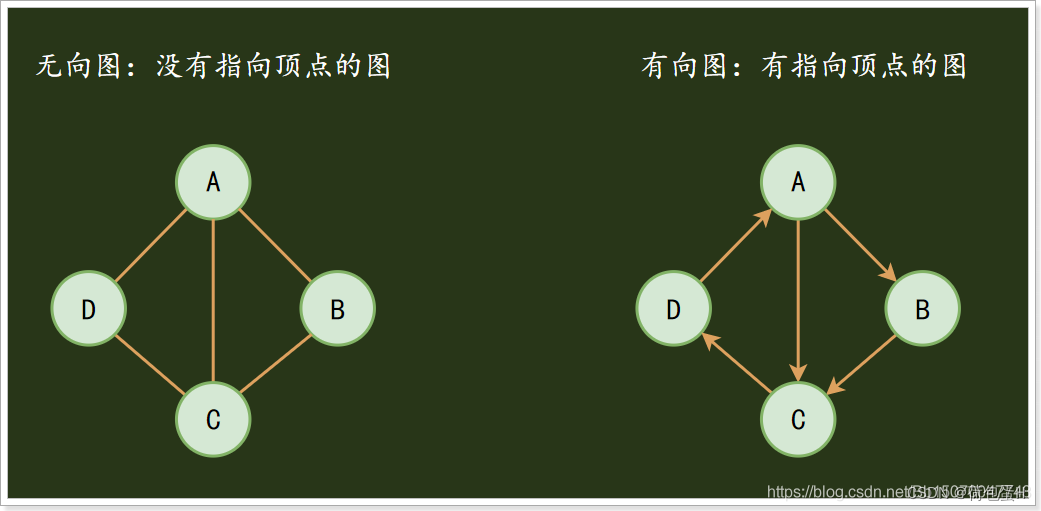
图是一种比较复杂的数据结构,在存储数据上有着比较复杂和高效的算法,分别有邻接矩阵 、邻接表、十字链表、邻接多重表、边集数组等存储结构。我们本次了解到这里即可;
四、mysql
1.mysql底层数据结构:B+树
1.1 索引的最左前缀原则:mysql建立多列索引(联合索引)有最左前缀的原则,即最左优先。
1.2 explain(sql执行计划):避免全表扫描,尽量走索引。
1) type: system > const > eq_ref > ref > range(范围) > index(索引) > all (性能好->差)