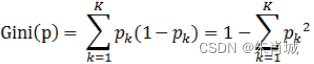https://leetcode.cn/problems/house-robber-iii/description/
前言
建议还是先看看动态规划的基础题再看这个。动态规划是不刷题,自己100%想不出来的。
基础题:
- 最大子数组和
- 乘积最大子数组
- 最长递增子序列
- 最大升序子数组和
小白想法
现在我们想遍历的数据结构不是数组了,而是一颗树。在树上的dp叫做“树形dp”(so called)。
那在遍历寻找解更新dp的时候无非就是用遍历树的dfs那一套了,不再是for i in range(length)了。
现在不方便用dp数组去存储dp的值了,毕竟这是个树。那用什么?我们之前之所以用数组,是因为使用dp[i]能够直接取到遍历到nums[i]时dp的值,之前的dp数组实际上充当的是一个hash table(字典、map…随便你怎么叫)的作用。 那我们就直接用字典就好啦!不再用数组了。
然后能不能像for i in range(length)一样“从前往后”边遍历边更新?树上的“从前往后”是什么?是从叶子走向根。
有了前几点的铺垫,下面正式进入状态转移方程的构建。
还能不能像以前“打家劫舍”那个题一样通过选择前几个状态来更新dp?
看上去好像可以。但是请注意我们现在的“dp数组”不是数组了,而是一个字典。字典的key是node,value是dp值。如果是数组,我们可以很方便的通过i-1,i-2指针来访问前面的状态,但是此时的字典已经不适合了。 当前的状态i和前面时刻-2的“联系”已经没有了。
题外话,莫非我可以先把“树形”的数据先压成一个数组,然后再套用之前的思路?想法很好,甚至也能做,但是写起来比较麻烦,下一个!
就算是有联系,在当前节点时,需要考虑 自己2个孩子是否被偷,没偷就有可能跟孙子一起被偷,共计6个节点,我相信写起来也挺复杂,要max很多次。
dead end after all…
题解,学习
换个dp数组的意义吧!我们不拘泥于过去的思路了。
在之前做“最大连乘子数组”的时候我们不是也用了2个dp数组吗?
把dp拆开成2个,分成 选择了子节点的最大值,和没选择了子节点的最大值。请注意树上的“从前往后”是从叶子到根。把这2个dp分别叫做dp_selected和dp_unselected。
先考虑最简单的情况,从最前面开始,只有一个叶子的时候,2个dp的值很好知道,叶子值或者0。
而当到了树上的分支now的时候,dp_selected[now]的意义是选择当前节点,那么应该等于自己当前节点的值+没选自己孩子的最大dp值:now.val+dp_unselected[now.left]+dp_unselected[now.right],只有这 一种情况,是因为相邻的父子不能一起选;而dp_unselected[now]就比较多了:由于我当前节点没选择,那么我的孩子可以选,也可以不选,那我要当前最大的,要取他们的最大值更新。
上面写的比较“大白话”,我个人感觉用数学公式表达起来比较简洁易懂。。
以下为官方题解
接下来就是遍历,然后通过转移方程一边遍历一边更新就行。
代码
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rob(self, root: Optional[TreeNode]) -> int:
# dp的存储形式变了,变成字典
# dp的意义变了,不再是“以xx结尾的结果”
from collections import defaultdict
dp_selected,dp_unselected=defaultdict(int),defaultdict(int)
def travel_tree(now):
if now is None:
return
travel_tree(now.left)
travel_tree(now.right)
left=now.left
right=now.right
res1=now.val+dp_unselected[left]+dp_unselected[right]
res2=max(dp_selected[left],dp_unselected[left])+max(dp_selected[right],dp_unselected[right])
dp_selected[now]=res1
# 可以选择不更新,因为不更新他就是0
# 在节点选择的过程中,0是肯定会被丢弃的
dp_unselected[now]=res2
return
travel_tree(root)
return max(dp_selected[root],dp_unselected[root])
defaultdict的作用是给予在dict中不存在的key一个初始值,简化代码。
提交,过了。
想不出来,不刷题真的想不出来。
优化
显然dp的hash table是很重要的,但是我们能不能把他也优化掉,不使用他的额外的空间呢?
我们可以从转移方程看到,当前点的更新只跟自己孩子的那几个值有关。
这熟悉的配方!在dp[i]只跟dp[i-1]有关时,我们也能通过类似的方法只保留上一个dp的值来优化空间。
那么怎么只保留上一个dp的值呢?我们上一个dp的值是“选左孩子的最大值”、“不选左孩子的最大值”、“选右孩子的最大值”、“不选右孩子的最大值”,一共4个,使用函数返回给父节点就可以了!(毕竟除了使用额外的空间,函数返回值是唯一父子能交流的东西了)
class Solution:
def rob(self, root: Optional[TreeNode]) -> int:
def travel_tree(now):
if now is None:
return 0, 0
l_rob, l_not_rob = travel_tree(now.left)
r_rob, r_not_rob = travel_tree(now.right)
rob = l_not_rob + r_not_rob + node.val # 选
not_rob = max(l_rob, l_not_rob) + max(r_rob, r_not_rob) # 不选
return rob, not_rob
return max(travel_tree(root)) # 根节点选或不选的最大值