一、介绍

        优化算法在机器学习和深度学习中至关重要，可以最小化损失函数，从而改善模型的预测。每个优化器都有其独特的方法来导航损失函数的复杂环境以找到最小值。本文探讨了一些最常见的优化算法，包括 Adadelta、Adagrad、Adam、AdamW、SparseAdam、Adamax、ASGD、LBFGS、NAdam、RAdam、RMSprop、Rprop 和 SGD，并提供了对其机制、优势和应用的见解。

在寻求学习的过程中，通过优化的每一步不仅会带来更好的模型，而且会带来对旅程本身的更深入理解。

二、技术背景

        大多数常用的方法已经得到支持，并且接口足够通用，因此将来也可以轻松集成更复杂的方法。

1. 随机梯度下降 （SGD）：随机梯度下降 （SGD） 是最基本但最有效的优化算法之一。它以与目标函数相对于参数的梯度相反的方向更新模型的参数。学习率决定了向最小值迈出的步数的大小。虽然 SGD 对于大型数据集来说简单而高效，但收敛速度可能很慢，并且可能在最小值附近振荡。
2. 动量和涅斯捷罗夫加速梯度 （NAG）：为了克服SGD的振荡和缓慢收敛，引入了动量和涅斯捷罗夫加速梯度（NAG）技术。它们通过将先前更新向量的一小部分添加到当前更新中来合并动量的概念。这种方法有助于在相关方向上加速 SGD 并抑制振荡，使其比标准 SGD 更快、更稳定。
3. Adagrad：Adagrad 通过使学习率适应参数，解决了适用于所有参数的全局学习率的限制。它对与频繁出现的要素相关的参数执行较小的更新，对与不频繁出现的要素相关的参数执行较大的更新。这种自适应学习率使 Adagrad 特别适用于稀疏数据。
4. Adadelta：Adadelta 是 Adagrad 的扩展，旨在降低其激进的、单调下降的学习率。Adadelta 不是累积所有过去的平方梯度，而是将累积的过去梯度的窗口限制为固定大小，使其对学习制度的变化更可靠。
5. RMSprop：RMSprop 修改了 Adagrad 的方法，通过引入衰减因子来累积以前的梯度，从而为最近的梯度赋予更多的权重。这使得它更适合在线和非平稳问题，类似于 Adadelta，但实现方式不同。
6. Adam（自适应力矩估计）：Adam 结合了 Adagrad 和 RMSprop 的优势，根据梯度的第一和第二矩调整每个参数的学习速率。该优化器因其在实践中的有效性而被广泛采用，尤其是在深度学习应用中。
7. AdamW：AdamW 是 Adam 的一个变体，它将权重衰减与优化步骤分离。这种修改提高了性能和训练稳定性，尤其是在深度学习模型中，其中权重衰减被用作正则化的一种形式。
8. SparseAdam：SparseAdam 是 Adam 的一个变体，旨在更有效地处理稀疏梯度。它使 Adam 算法仅在必要时更新模型参数，因此对于自然语言处理 （NLP） 和其他具有稀疏数据的应用程序特别有用。
9. Adamax：Adamax 是基于无穷范数的 Adam 的变体。它对梯度中的噪声更鲁棒，并且在某些情况下可能比 Adam 更稳定，尽管它不太常用。
10. ASGD（平均随机梯度下降）：ASGD 会随时间推移对参数值进行平均，这可以在训练结束时实现更平滑的收敛。此方法对于具有嘈杂或波动梯度的任务特别有用。
11. LBFGS（有限内存 Broyden-Fletcher-Goldfarb-Shanno）：LBFGS 是准牛顿方法系列中的一种优化算法。它近似于 Broyden-Fletcher-Goldfarb-Shanno （BFGS） 算法，使用有限的内存量。由于其内存效率，它非常适合中小型优化问题。
12. NAdam（涅斯捷罗夫加速自适应力矩估计）：NAdam 将 Nesterov 加速梯度与 Adam 相结合，将 Nesterov 动量的 lookahead 属性纳入 Adam 的框架中。这种组合通常可以提高性能并加快收敛速度。
13. 拉丹（纠正亚当）： RAdam 在 Adam 优化器中引入了一个整流项来动态调整自适应学习率，解决了一些与收敛速度和泛化性能相关的问题。它提供了更稳定和一致的优化环境。
14. Rprop（弹性反向传播）：Rprop 仅使用梯度符号调整每个参数的更新，忽略其幅度。这使得它对梯度幅度变化很大但不太适合小批量学习或深度学习应用的问题非常有效。

三、相关代码

        创建一个完整的 Python 示例来演示如何在合成数据集上使用这些优化器涉及几个步骤。我们将使用一个简单的回归问题作为示例，其中的任务是从特征预测目标变量。此示例将涵盖创建合成数据集、使用 PyTorch 定义简单神经网络模型、使用每个优化器训练此模型，以及绘制训练指标以比较其性能。

import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# Generate synthetic data
np.random.seed(42)
X = np.random.rand(1000, 1) * 5  # Features
y = 2.7 * X + np.random.randn(1000, 1) * 0.9  # Target variable with noise

# Convert to torch tensors
X = torch.from_numpy(X).float()
y = torch.from_numpy(y).float()

# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

class LinearRegressionModel(nn.Module):
    def __init__(self):
        super(LinearRegressionModel, self).__init__()
        self.linear = nn.Linear(1, 1)  # One input feature and one output

    def forward(self, x):
        return self.linear(x)

def train_model(optimizer_name, learning_rate=0.01, epochs=100):
    model = LinearRegressionModel()
    criterion = nn.MSELoss()
    
    # Select optimizer
    optimizers = {
        "SGD": optim.SGD(model.parameters(), lr=learning_rate),
        "Adadelta": optim.Adadelta(model.parameters(), lr=learning_rate),
        "Adagrad": optim.Adagrad(model.parameters(), lr=learning_rate),
        "Adam": optim.Adam(model.parameters(), lr=learning_rate),
        "AdamW": optim.AdamW(model.parameters(), lr=learning_rate),
        "Adamax": optim.Adamax(model.parameters(), lr=learning_rate),
        "ASGD": optim.ASGD(model.parameters(), lr=learning_rate),
        "NAdam": optim.NAdam(model.parameters(), lr=learning_rate),
        "RAdam": optim.RAdam(model.parameters(), lr=learning_rate),
        "RMSprop": optim.RMSprop(model.parameters(), lr=learning_rate),
        "Rprop": optim.Rprop(model.parameters(), lr=learning_rate),
    }
    
    if optimizer_name == "LBFGS":
        optimizer = optim.LBFGS(model.parameters(), lr=learning_rate, max_iter=20, history_size=100)
    else:
        optimizer = optimizers[optimizer_name]

    train_losses = []

    for epoch in range(epochs):
        def closure():
            if torch.is_grad_enabled():
                optimizer.zero_grad()
            outputs = model(X_train)
            loss = criterion(outputs, y_train)
            if loss.requires_grad:
                loss.backward()
            return loss
        
        # Special handling for LBFGS
        if optimizer_name == "LBFGS":
            optimizer.step(closure)
            with torch.no_grad():
                train_losses.append(closure().item())
        else:
            # Forward pass
            y_pred = model(X_train)
            loss = criterion(y_pred, y_train)
            train_losses.append(loss.item())

            # Backward pass and optimize
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()
    
    # Test the model
    model.eval()
    with torch.no_grad():
        y_pred = model(X_test)
        test_loss = mean_squared_error(y_test.numpy(), y_pred.numpy())

    return train_losses, test_loss

optimizer_names = ["SGD", "Adadelta", "Adagrad", "Adam", "AdamW", "Adamax", "ASGD", "LBFGS", "NAdam", "RAdam", "RMSprop", "Rprop"]

plt.figure(figsize=(14, 10))

for optimizer_name in optimizer_names:
    train_losses, test_loss = train_model(optimizer_name, learning_rate=0.01, epochs=100)
    plt.plot(train_losses, label=f"{optimizer_name} - Test Loss: {test_loss:.4f}")

plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.title("Training Loss by Optimizer")
plt.legend()
plt.show()

Notes:

• 为简单起见，所有优化器都使用 0.01 的默认学习率。调整学习率和其他超参数可能会导致不同的性能结果。
• 为了完整性，包含优化器，但通常用于具有稀疏梯度的模型，这可能不适用于此简单线性回归示例。SparseAdam
• 由于其行搜索方法，优化器需要的训练循环略有不同。提供的训练功能可能需要修改才能正确使用 。LBFGSLBFGS

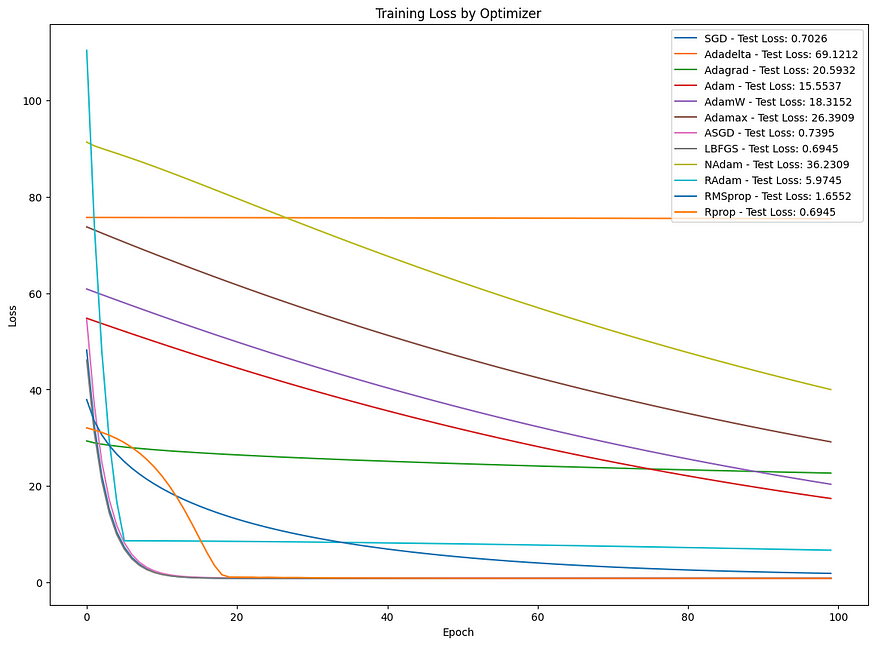
        此示例基本比较了不同优化器在简单合成数据集上的表现。对于更复杂的模型和数据集，优化器之间的差异可能更明显，优化器的选择会显著影响模型性能。

四、结论

        总之，每个优化器都有其优点和缺点，优化器的选择可以显着影响机器学习模型的性能。选择取决于具体问题、数据的性质和模型体系结构。了解这些优化器的基本机制和特征对于有效地将它们应用于各种机器学习挑战至关重要。