六、矩阵问题

73、矩阵置零（中等）

题目描述

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用原地算法。

示例 1：

输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

示例 2：

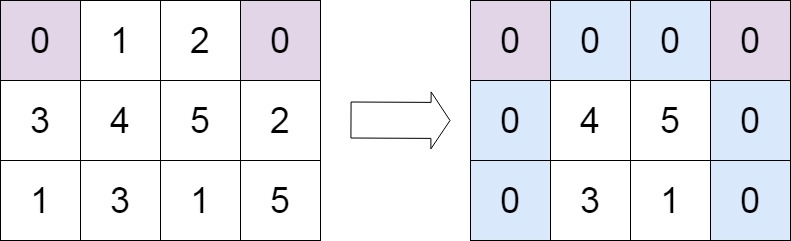
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

提示：

m == matrix.length
n == matrix[0].length
1 <= m, n <= 200
-2³¹ <= matrix[i][j] <= 2³¹ - 1

进阶：

一个直观的解决方案是使用 O(mn) 的额外空间，但这并不是一个好的解决方案。
一个简单的改进方案是使用 O(m + n) 的额外空间，但这仍然不是最好的解决方案。
你能想出一个仅使用常量空间的解决方案吗？

题目思路

对于这道题，要求将一个矩阵中含有0的位置，该行和该列都设置为0。

这道题有点类似于炸弹人的游戏机制，炸弹将一行和一列全部炸裂了。
说到这道题，如果没有空间的限制，很容易实现。

如果是O(mn)，非常简单，新开辟一个新的矩阵即可。
如果是O(m+n)，也不是很困难，我们利用额外的空间记录对应的行和列是否为0即可。

而如果是常量的空间复杂度，就较为麻烦了，这就需要我们利用现有的空间来记录信息——即使用当前的数组来记录信息。

因此这里，我们的思路是使用当前矩阵的第一行和第一列来记录对应的行和列是否应该为0。

不过这里有一个问题：

如果第一行和第一列本身就有0，那么这样的记录就会造成 “污染”，因此，这里我们需要对第一行和第一列做单独的判断。

在算法流程上：

判断第一行和第一列是否应该为0；
从(1, 1)开始，自上而下、自左向右判断元素num[i][j]是否为0——如果为0，就设置num[i][0]和num[0][j]为0；
再次遍历，根据对应第一行和第一列元素的值，对当前的值进行赋值——如果标记为0，则置为0；
最后，根据第一步的判断结果，对第一行和第一列更新数据；

算法代码

1、O(m+n)

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        zero_row, zero_col = [], []
        m, n = len(matrix), len(matrix[0])
        
        for i in range(m):
            for j in range(n):
                if matrix[i][j] == 0:
                    zero_row.append(i)
                    zero_col.append(j)

        for r in zero_row:
            for j in range(n):
                matrix[r][j] = 0
                
        for c in zero_col:
            for i in range(m):
                matrix[i][c] = 0

2、常量空间

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        is_first_row_zero, is_first_col_zero = False, False
        m, n = len(matrix), len(matrix[0])

        for i in range(m):
            if matrix[i][0] == 0:
                is_first_col_zero = True
                break
        for j in range(n):
            if matrix[0][j] == 0:
                is_first_row_zero = True
                break

        for i in range(1, m):
            for j in range(1, n):
                if matrix[i][j] == 0:
                    matrix[i][0] = 0
                    matrix[0][j] = 0

        for i in range(1, m):
            for j in range(1, n):
                if matrix[i][0] == 0 or matrix[0][j] == 0:
                    matrix[i][j] = 0

        if is_first_col_zero:
            for i in range(m):
                matrix[i][0] = 0

        if is_first_row_zero:
            for j in range(n):
                matrix[0][j] = 0

54、螺旋矩阵（中等）

题目描述

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 10
-100 <= matrix[i][j] <= 100

题目思路

对于这道题，要求我们按照顺时针的方向对矩阵进行遍历，最后转化为一维数组。
在进行数组展开时，我们可以看到顺序是：

向右->向下->向左->向上

如果直接去模拟，整个过程较为繁琐，需要定义每个方向要走多少步等。
这里，我们通过不断重新定义矩阵上下左右边界的方法，来实现循环遍历。

算法具体步骤：

初始化矩阵的上下左右边界；
在上边界（即第一行）从最左移动到最右，此时第一行遍历完后相当于已经用过了，因此可以直接从图中删去，即重新定义上边界（top+1）；
- 若重新定义上边界后，上、下边界交错（top > bottom），说明此时矩阵遍历结束，直接跳出循环，返回结果即可；
- 若上下不交错，则继续在最右边界处，从最上遍历到最下，逻辑同理；
不断循环上述步骤，直到其中某两条边界交错，跳出循环，返回结果；

算法代码

class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        res = []
        # 定义矩阵上下边界
        top, bottom = 0, len(matrix) - 1
        # 定义矩阵左右边界
        left, right = 0, len(matrix[0]) - 1
        while True:
            # 在上边界，从最左遍历到最右
            for i in range(left, right+1):
                res.append(matrix[top][i])
            # 重新设置上边界，如果上边界大于下边界，说明遍历完成，下同
            top += 1
            if top > bottom:
                break
            # 在右边界，从最上遍历到最下
            for i in range(top, bottom+1):
                res.append(matrix[i][right])
            right -= 1
            if right < left:
                break
            # 在下边界，从最右遍历到最左
            for i in range(right, left-1, -1):
                res.append(matrix[bottom][i])
            bottom -= 1
            if bottom < top:
                break
            # 在左边界，从最下遍历到最上
            for i in range(bottom, top-1, -1):
                res.append(matrix[i][left])
            left += 1
            if left > right:
                break

        return res

48、旋转图像（中等）

题目描述

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

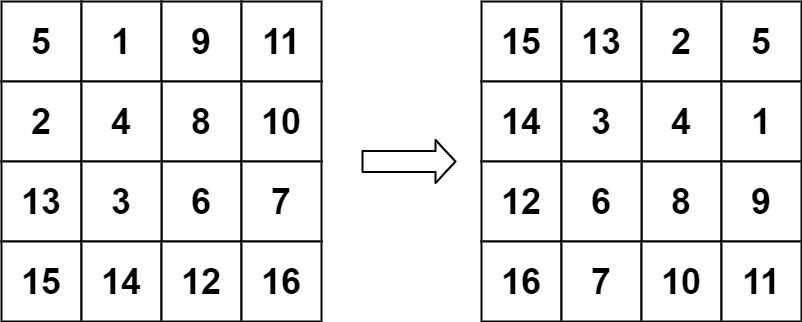
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

提示：

n == matrix.length == matrix[i].length
1 <= n <= 20
-1000 <= matrix[i][j] <= 1000

题目思路

对于这道题，本质上是要求我们将一个二维n*n矩阵顺时针旋转90度。

如果我们可以使用额外空间，比较简单直接：

对于矩阵中第i行第j个元素，旋转后，会出现在倒数第i列的第j个位置：
- matrix_new[j][n - i - 1] = matrix[i][j]

但题目这里不允许使用额外的空间，因此这里我们需要在原二维矩阵进行操作，这里可以直接通过翻转得到。

顺时针旋转：
- 先通过水平轴翻转，再根据主对角线翻转；
逆时针旋转：
- 先通过垂直轴翻转，再根据主对角线旋转；

顺时针：

 1 2 3     7 8 9     7 4 1
 4 5 6  => 4 5 6  => 8 5 2
 7 8 9     1 2 3     9 6 3

逆时针：

 1 2 3     3 2 1     3 6 9
 4 5 6  => 6 5 4  => 2 5 8
 7 8 9     9 8 7     1 4 7

以顺时针为例，之所以能够通过两次翻转得到，是由于：
1、水平轴翻转：

matrix[row][col] => matrix[n-row-1][col]

2、主对角线翻转：

matrix[n-row-1][col] => matrix[col][n-row-1]

因此最终可以得到：

matrix_new[j][n - i - 1] = matrix[i][j]

算法代码

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        matrix.reverse()
        for i in range(len(matrix)):
            for j in range(i+1, len(matrix)):
                matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]

附带逆时针：

class Solution48:
    def rotate(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        matrix = [list(reversed(x)) for x in matrix]
        for i in range(len(matrix)):
            for j in range(i+1, len(matrix)):
                matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]

240、搜索二维矩阵 II（中等）

题目描述

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。

示例 1：

输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

示例 2：

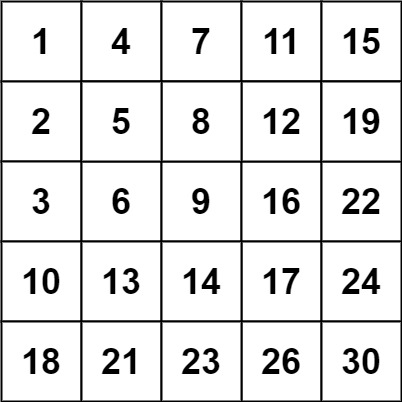
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false

提示：

m == matrix.length
n == matrix[i].length
1 <= n, m <= 300
-10⁹ <= matrix[i][j] <= 10⁹
每行的所有元素从左到右升序排列
每列的所有元素从上到下升序排列
-10⁹ <= target <= 10⁹

题目思路

对于这道题，要求我们在一个二维数组中找到目标值。

首先，我们可以直接使用暴力搜索的

不过在这道题中该二维数组具备：

每行的元素从左到右升序排列；
每列的元素从上到下升序排列；

因此，我们可以从矩阵的右上角(0, n-1)进行从右向左、从上到下进行查找。

这是由于如果我们从左上角开始，如果matrix[x][y]小于target，那么下一个查找的数字既有可能在右边、也有可能在下边，查找起来就很麻烦。

然而如果我们从右上角开始查找：

如果matrix[x][y] == target，说明查找完成；
如果matrix[x][y] > target，由于每一列的元素都是升序排列的，那么在当前的搜索矩阵中，所有位于第 y 列的元素都是严格大于 target 的，因此我们可以将它们全部忽略，即将 y-1；
如果matrix[x][y] < target，由于每一行的元素都是升序排列的，那么在当前的搜索矩阵中，所有位于第 x 行的元素都是严格小于 target 的，因此我们可以将它们全部忽略，即将 x+1。

在搜索的过程中，如果我们超出了矩阵的边界，那么说明矩阵中不存在 target。

算法代码

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        m, n = len(matrix), len(matrix[0])
        x, y = 0, n-1
        while x < m and y >= 0:
            if matrix[x][y] == target:
                return True
            elif matrix[x][y] > target:
                y -= 1
            else:
                x += 1
        return False