目录

一、常用排序算法比较

二、快速选择算法

快速选择

图解快速选择

三、代码实现

---

一、常用排序算法比较

排序	时间复杂度	空间复杂度	稳定性
插入排序	O(n²)	O(1)	稳定
希尔排序	O(nlogn)-O(n²)取决于增量序列	O(1)	不稳定
选择排序	O(n²)	O(1)	不稳定
冒泡排序	O(n²)	O(1)	稳定
堆排序	O(nlogn)	O(1)	不稳定
归并排序	O(nlogn)	O(n)	稳定
快速排序	O(nlogn)	O(logn)-O(n)取决于递归深度	不稳定

二、快速选择算法

快速选择

快速选择算法（Quickselect）是用于在未排序的数组中查找第k小或第k大元素的高效算法，它的时间复杂度为O(n)。该算法与快速排序有密切的联系，但它不对整个数组进行完整的排序，而是只关注于找到所需的特定顺序的元素。以下是它的一些关键点：

1. 基本思想：

• 选择一个基准值（pivot），按照这个基准值将数组分为两部分，左侧部分的所有元素都小于等于基准值，右侧部分的所有元素都大于基准值。

1. 递归搜索：

• 确定基准值的位置后，根据k与基准值的位置关系，选择数组的哪一部分继续进行递归搜索。如果k小于基准值的索引，则在第一部分（小于等于基准值的部分）继续搜索；否则，在第二部分（大于基准值的部分）继续搜索。

1. 时间复杂度：

• 快速选择算法的平均时间复杂度为O(n)，但最坏情况下的时间复杂度会退化到O(n^2)。尽管如此，由于其不需要完全排序数组，它在实际操作中通常比完全的排序算法更加高效。

1. 实际应用：

• 快速选择算法及其变种是在实际应用中最常使用的高效选择算法之一，尤其适用于解决Top K问题等场景。

总的来说，快速选择算法是一种基于快速排序的选择算法，它高效地解决了在不完全排序的数组中寻找特定顺序元素的问题，并因此在各种算法竞赛和实际应用场景中得到了广泛的使用。

图解快速选择

图解

对下面这个数组寻找到前k小的元素

首先我随机生成一个下标指向一个基准元素

然后使用一个指针指向开始位置依次往后遍历，如果当前元素比基准元素大则将该元素放在末尾，也就是基准元素后面，如果比当前元素小则将他放在基准元素前面

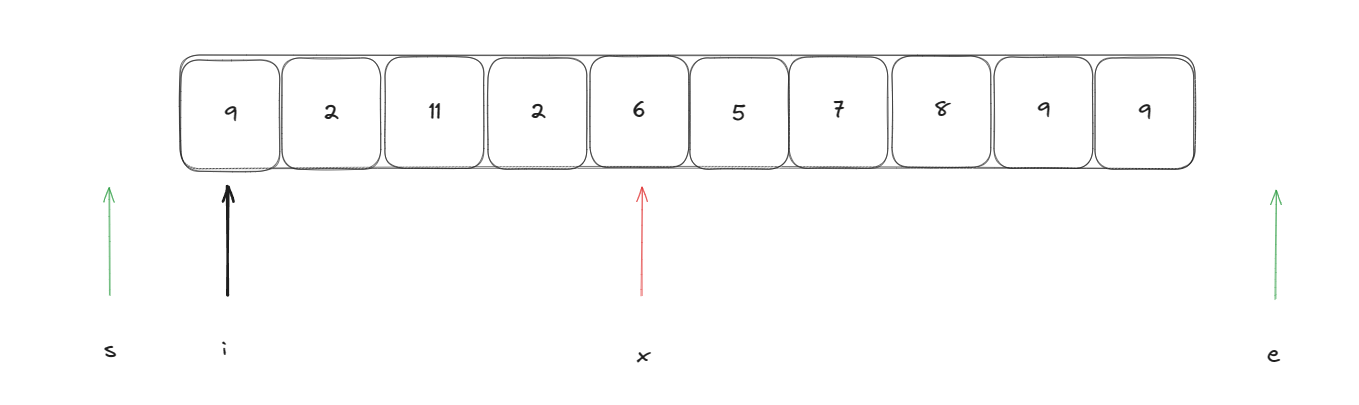
此时遍历指针i指向的值比基准元素大，此时需要执行以下操作进行交换：swap(arr[--e], arr[i])

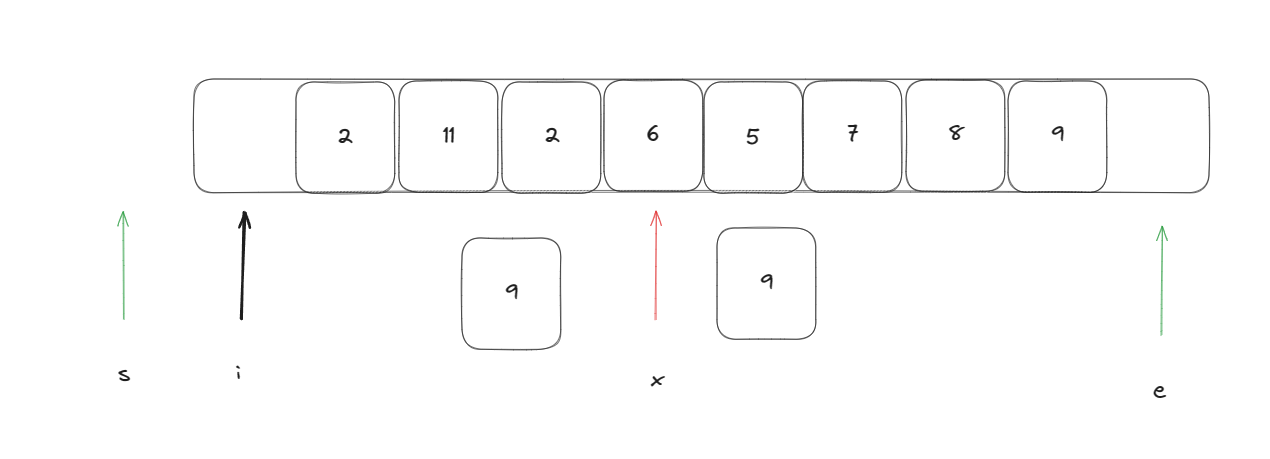
此时进行将遍历指针指向的元素与基准元素进行比较依次重复此操作，当遍历指针指向的元素比基准元素小时执行：swap(arr[i++], arr[++s]) ,当与基准元素相等时只需要执行i++即可。当遍历指针与末尾指针e相遇时即可停止。

此时在l到s，e到r重复执行上述操作，知道l >= r时结束递归就是基于快速选择的快排算法。

三、代码实现

import java.util.ArrayList;
import java.util.Random;
import java.util.Scanner;

public class BigNumber {
    private static int random(int l, int r) {
        Random random = new Random();
        return random.nextInt(r - l + 1) + l;
    }

    private static void swap(int[] arr, int i, int j) {
        int t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;
    }

    private static void qSort(int[] arr, int l, int r) {
        if (l >= r) return;
        int i = l, s = l - 1, e = r + 1, x = arr[random(l, r)];
        while (i < e) {
            if (arr[i] > x) swap(arr, --e, i);
            else if (arr[i] < x) swap(arr, i++, ++s);
            else i++;
        }
        qSort(arr, l, s);
        qSort(arr, e, r);
    }

    public static void main(String[] args) {
        int[] arr = {5,6,7,2,4,5,5,5};
        qSort(arr, 0, arr.length - 1);
        for (int x : arr) System.out.println(x);
    }
}

#include <iostream>
#include <cmath>
#include <cstring>
#include <vector>
#include <algorithm>

using namespace std;
typedef long long ll;

int random(int l, int r) {
    srand(time(0));
    return rand() % (r - l + 1) + l;
}

void qsort(vector<int>& arr, int l, int r) {
    if (l >= r) return;
    int i = l, s = l - 1, e = r + 1, x = arr[random(l, r)];
    while (i < e) {
        if (arr[i] > x) swap(arr[i], arr[--e]);
        else if (arr[i] < x) swap(arr[i++], arr[++s]);
        else i++;
    }
    qsort(arr, l, s), qsort(arr, e, r);
}

int main() {
    vector<int> arr = {7,6,6,6,5,5,4,3,2,1};
    qsort(arr, 0 ,arr.size() -1);
    for (auto x : arr) cout << x << endl;
}