性能优越！|多策略改进的长鼻浣熊优化算法MSCOA（MATLAB）

文章来源于我的个人公众号：KAU的云实验台，主要更新智能优化算法的原理、应用、改进

函数测试(部分)：

在这里插入图片描述

仅运行MSCOA:
在这里插入图片描述

所有元启发式算法的共同点在于，其搜索过程可分为勘探和开发两个阶段。勘探阶段指算法对全局空间的搜索能力，决定了算法能否获得最优解；开发阶段指对局部空间的搜索能力，决定了算法获得最优解的速度。勘探和开发之间的平衡做的越好，算法的性能就越好。而由没有免费的午餐（NFL）定理可知，没有元启发式优化算法可以处理所有的优化问题，在某些情况下(可结合应用)，由于种群多样性不足，算法会陷入局部最优解，同样，COA[1]也有以上问题，因此本文将对其进行改进，并针对COA的改进算法进行函数测试，源码为Matlab所写。

00 目录

1 长鼻浣熊优化 (COA) 算法原理

2 多策略改进的长鼻浣熊优化算法原理

3 代码目录

4 算法性能

5 源码获取

01 长鼻浣熊优化 (COA)算法原理

在上一篇文章中KAU介绍了长鼻浣熊算法的原理及其代码实现

02 多策略改进的长鼻浣熊优化算法原理

2.1 初始化种群的改进

2.1.1 初始种群多样化

COA通过随机生成初始种群的方法，容易出现种群分布不均匀，会导致种群多样性减少，种群质量不高，影响算法的收敛速度。

佳点集是一种有效的均匀选点方法。该理论由华罗庚先生提出[2]，在许多群智能优化算法中都得到了应用，由佳点集的定义，设GD是D维欧式空间中的单位立方体，若r∈GD，形为：

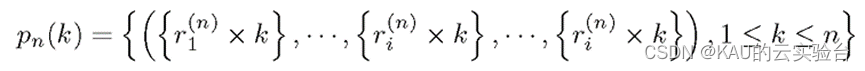
在这里插入图片描述

其偏差满足：

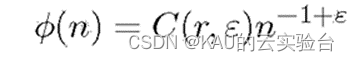
在这里插入图片描述

则称Pn(k)为佳点集，r为佳点，其中C(r, ε)是是只与r、ε(ε>0)有关的常数。取rk={2cos(2pir/p)}，1≤k≤n，p是满足(p-D/2)≥D的最小素数，理论上已证明，用n个佳点构成的加权和比采用任何其他n个点所得到的误差都要小，并尤其适用于高维空间的近似计算。以二维单位搜索空间为例，随机取点与佳点集方法取点的对比如下：
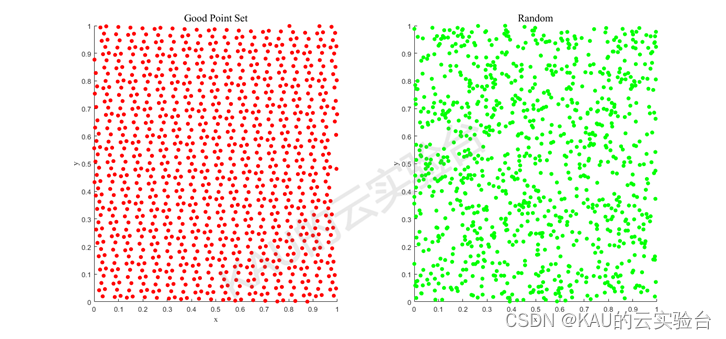
在这里插入图片描述

显然,随机取点并不均匀，并且许多取点位置重合，会造成解的可利用率不高，而佳点集方法能够使得取点更为均匀地分布在搜索空间中，其在全局中的搜索效率将更高。

2.1.2 初始种群精英化

反向学习策略是由TIZHOOSH于2005年提出[3]，在当前个体区域内生成相反个体，对比选取适应度高的个体进行后续迭代，可以有效提高种群的质量及多样性，加强算法的搜索能力。

然而，反向学习策略产生的反向解与当前解的距离值固定，缺乏一定的随机性，可能导致搜索空间内的种群多样性无法有效增加，因此本文采用动态反向学习策略来进一步增加算法种群的多样性和种群精英个体的数量[4]，帮助算法扩大搜索区域，从而提高选取更优解的概率，其数学模型如下：
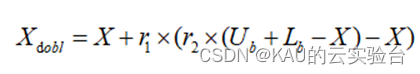
在这里插入图片描述

式中，Xdobl为动态反向解；r1和r2为(0,1)之间的随机数；X为当前解。

2.2 融合黄金正弦的勘探阶段

黄金正弦算法（Golden Sine Algorithm，Golden-SA）是Tanyildizi等人于2017年提出的一种新型元启发式算法[5]，其依据正弦函数与单位圆的关系，可以遍历正弦函数上的所有点即单位圆上的所有点，算法具有较强的全局搜索能力，且Golden-SA在其位置更新过程中引入了黄金分割数系数，使得算法在每次迭代过程中都会对能产生优秀解的区域进行充分搜索，从而加快了算法的收敛速度，跳出局部最优。

在这里插入图片描述

因此本文将黄金正弦策略融入COA的勘探阶段中，增强算法的全局搜索能力，具体数学模型这里不作展示。

2.3 引入哈里斯鹰包围的开发阶段

由前一篇文章对长鼻浣熊算法COA的分析可知，COA的开发缺乏最佳信息的引导，可能不利于后期的快速收敛，因此其开发阶段的更新公式存在改善的空间。而哈里斯鹰算法HHO在开发阶段的软硬包围以及快速俯冲策略具有强健的局部搜索性能，如果将HHO和COA结合，算法将获得更好的性能，因此本文将HHO的开发阶段引入，通过猎物能量选择软包围或硬包围，并根据适应度判断使用莱维游走还是快速俯冲攻击，使算法能够有效跳出局部最优。

HHO采用四种策略来模仿哈里斯鹰的狩猎行为，这四种策略分别是软包围、硬包围、渐进式快速俯冲的软包围和渐进式快速俯冲的硬包围。本文将这些策略引入COA的开发中。

2.4 基于无序维度采样的纵横交叉

在标准COA算法的后期迭代中，种群个体将向最优个体聚集，其适应度值将趋于稳定，容易导致搜索停滞，种群陷入局部最优。为提高COA算法的计算精度以及跳出局部最优的能力，对当前个体的“变异”策略是行之有效的方法。

本文采样纵横交叉策略[6]对个体进行修正，利用横向交叉对种群进行交叉搜索以减少搜索盲点，通过纵向交叉增加种群多样性的同时降低算法陷入局部最优的概率。

然而，纵横交叉策略虽然拥有优异的搜索性能，但全维度的交叉运算将极大地增加计算负担，面对高维问题，其计算成本将几何倍增加，因此本文采用一种无序维度采样的方法，减少计算成本的同时也能防止由于减少接近最佳个体的维数而减少总体稀疏性。

2.4.1 无序维度采样

采样率决定了纵横交叉所涉及的维度数量，所涉及的维度是通过采样率选择的

2.4.2 横向交叉

横向交叉是指从种群的同一维度中选择两个个体，按照一定的随机比例交换个体信息，产生自己的后代，通过适者生存来更新个体的位置，以提高算法的全局寻优性能。

2.4.3 纵向交叉

纵向交叉是指种群中最佳个体的不同维度之间，按照一定的纵向交叉概率交换维度信息，从而产生新一代最优秀的个体与父代竞争，有利于不同维度相互学习，避免某个维度的过早收敛。

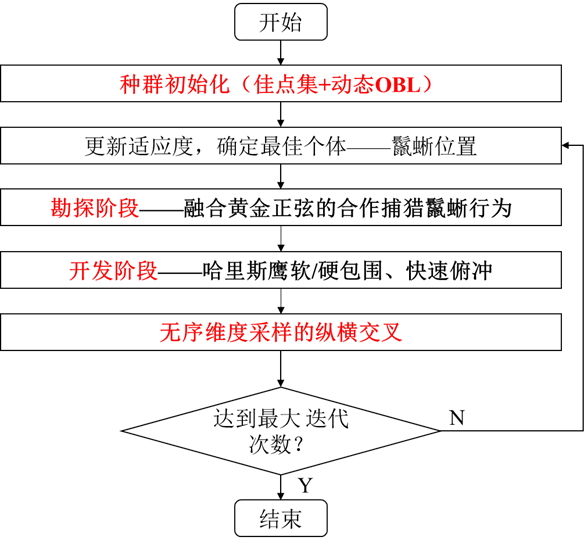
2.5 算法流程

该算法的的程图如下：

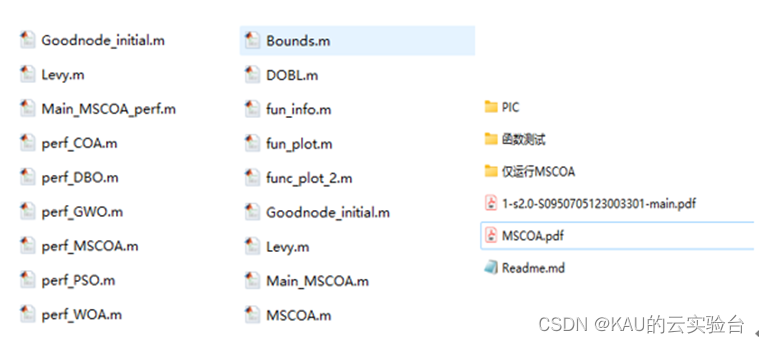
在这里插入图片描述

03 代码目录

在这里插入图片描述

(左:函数测试文件夹，中:仅运行MSCOA，右:文件一览)

MATLAB编写，文件含完整改进算法理论说明，并在Readme文件中对各文件夹内容作了说明：
在这里插入图片描述

代码都经过作者重新注释，代码清爽，可读性强。

04 算法性能

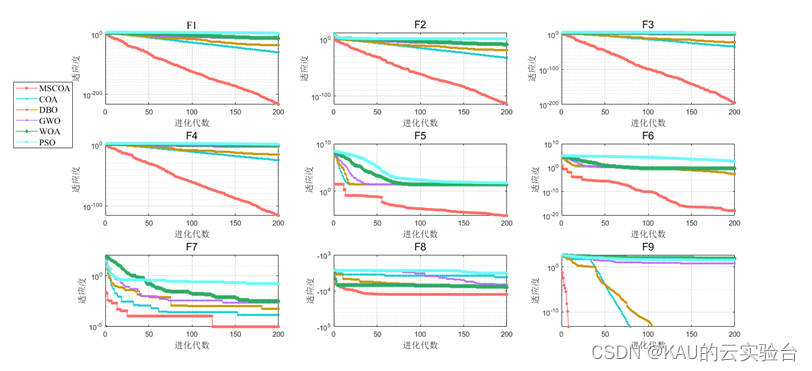
采用CEC2005测试函数检验改进的COA优化算法性能。

在MATLAB中，进行标准函数的测试，执行程序结果如下：

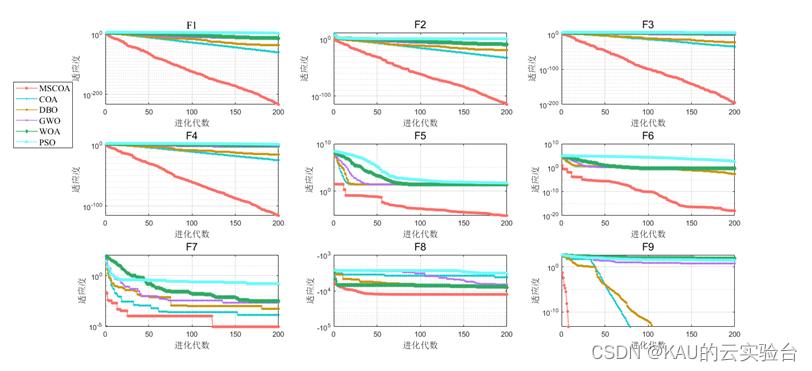
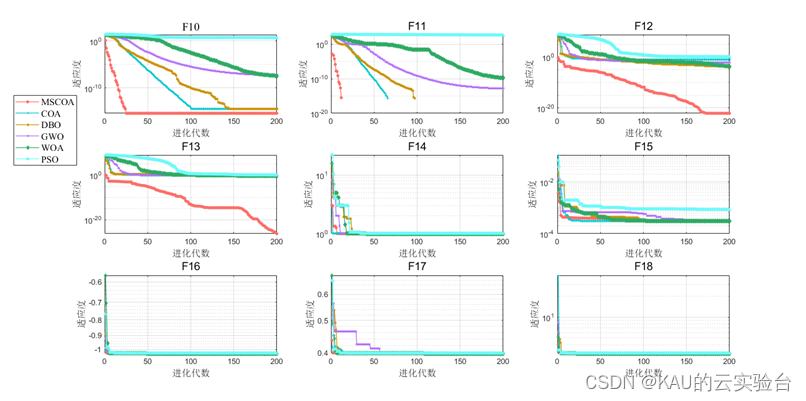
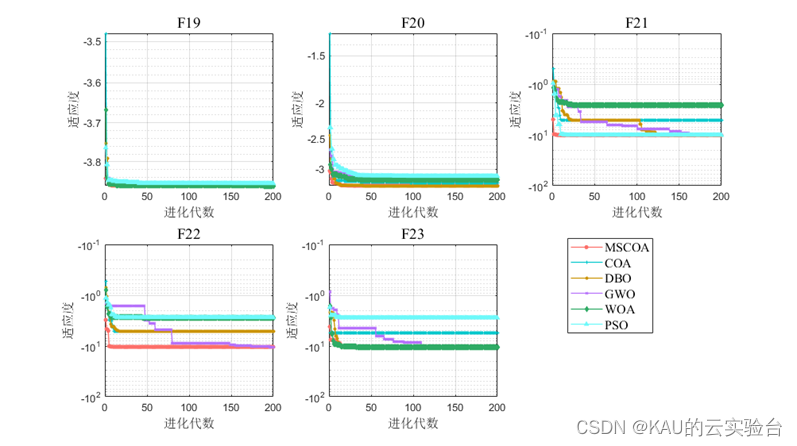
函数测试：（包含迭代曲线对比、均值/方差/最优对比、箱型图对比）

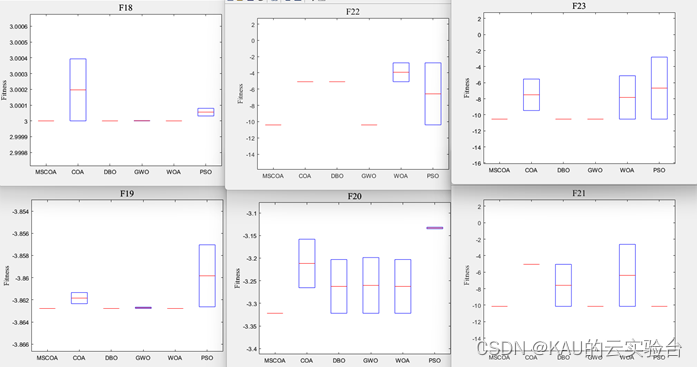
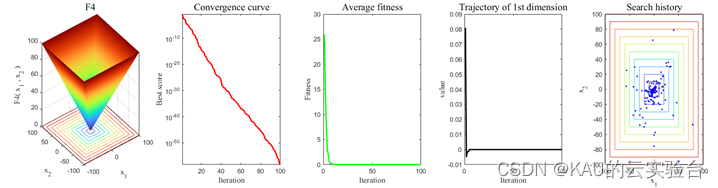
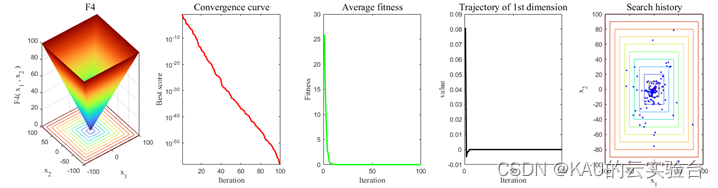
在这里插入图片描述

仅运行MSCOA：（包含函数三维图、迭代曲线、平均迭代曲线、1维轨迹、搜索历史）
在这里插入图片描述

05 源码获取

在公众号:KAU的云实验台 回复 MSCOA

参考文献

[1] DEHGHANI M, MONTAZERI Z, TROJOVSKÁ E, et al.Coati Optimization Algorithm: a new bio-inspired metaheuristic algorithm for solving optimization problems[J].Knowledge-based systems, 2023, 259: 110011.

[2] 华罗庚,王元.数论在近似分析中的应用[M].北京:科学出版社. 1978: 83-86.Hua LG,Wang Y.Application of number theory in approximate analysis[M. Beijing: Science Press，1978:83-86.

[3] TIZHOOSH H R. Opposition-based Learning: A New Scheme for Machine Intelligence[C]//IEEE. Proceedings of Computational Intelligence for Modelling, November 28-30, 2005, Vienna, Austria. New York: IEEE, 2005: 695-701.

[4]Yan Ai-jun, Hu Kai-cheng. Improved strategy and its application to the Optimization of seagull optimization algorithm[J]. Information and Control, 2022, 51(6): 688-698.

[5] TANYILDIZI E，DEMIR G.Golden sine algorithm：a novel math-inspired algorithm[J].Advances in Electrical &Computer Engineering，2017，17（2）：71-78.

[6] Meng A, Chen Y,Yin H,et al. Crisscross optimization algorithm and its application [ J ]. Knowledge Based Systems, 2014,67 (4 )：218-229.

另：如果有伙伴有待解决的优化问题（各种领域都可），可以发我，我会选择性的更新利用优化算法解决这些问题的文章。

如果这篇文章对你有帮助或启发，可以点击右下角的赞/在看(ง •̀_•́)ง(不点也行)，你们的鼓励就是我坚持的动力！若有定制需求，可私信作者。