目录:
- 第一题. 百万级别或以上的数据如何删除?
- 第二题. 前缀索引
- 第三题. 什么是最左前缀原则?什么是最左匹配原则?
- 第四题. B树和B+树的区别
- 第五题. 使用B树和B+树好处
第一题. 百万级别或以上的数据如何删除?
关于索引:由于索引需要额外的维护成本,因为索引文件是单独存在的文件,所以当我们对数据的增加,修改,删除,都会产生额外的对索引文件的操作,这些操作需要消耗额外的IO,会降低增/改/删的执行效率。所以,在我们删除数据库百万级别数据的时候,查询MySQL官方手册得知删除数据的速度和创建的索引数量是成正比的。
- 所以我们想要删除百万数据的时候可以先删除索引(此时大概耗时三分多钟)
- 然后删除其中无用数据(此过程需要不到两分钟)
- 删除完成后重新创建索引(此时数据较少了)创建索引也非常快,约十分钟左右。
- 与之前的直接删除绝对是要快速很多,更别说万一删除中断,一切删除会回滚。那更是坑了。
第二题. 前缀索引
语法:index(field(10)),使用字段值的前10个字符建立索引,默认是使用字段的全部内容建立索引。
前提:前缀的标识度高。比如密码就适合建立前缀索引,因为密码几乎各不相同。
实操的难度:在于前缀截取的长度。
我们可以利用select count(*)/count(distinct left(password,prefixLen));,通过从调整prefixLen的值(从1自增)查看不同前缀长度的一个平均匹配度,接近1时就可以了(表示一个密码的前prefixLen个字符几乎能确定唯一一条记录)
第三题. 什么是最左前缀原则?什么是最左匹配原则?
- 顾名思义,就是最左优先,在创建多列索引时,要根据业务需求,where子句中使用最频繁的一列放在最左边。
- 最左前缀匹配原则,非常重要的原则,mysql会一直向右匹配直到遇到范围查询(>、<、between、like)就停止匹配,比如a = 1 and b = 2 and c > 3 and d = 4如果建立(a,b,c,d)顺序的索引,d是用不到索引的,如果建立(a,b,d,c)的索引则都可以用到,a,b,d的顺序可以任意调整。
- =和in可以乱序,比如a = 1 and b = 2 and c = 3 建立(a,b,c)索引可以任意顺序,mysql的查询优化器会帮你优化成索引可以识别的形式
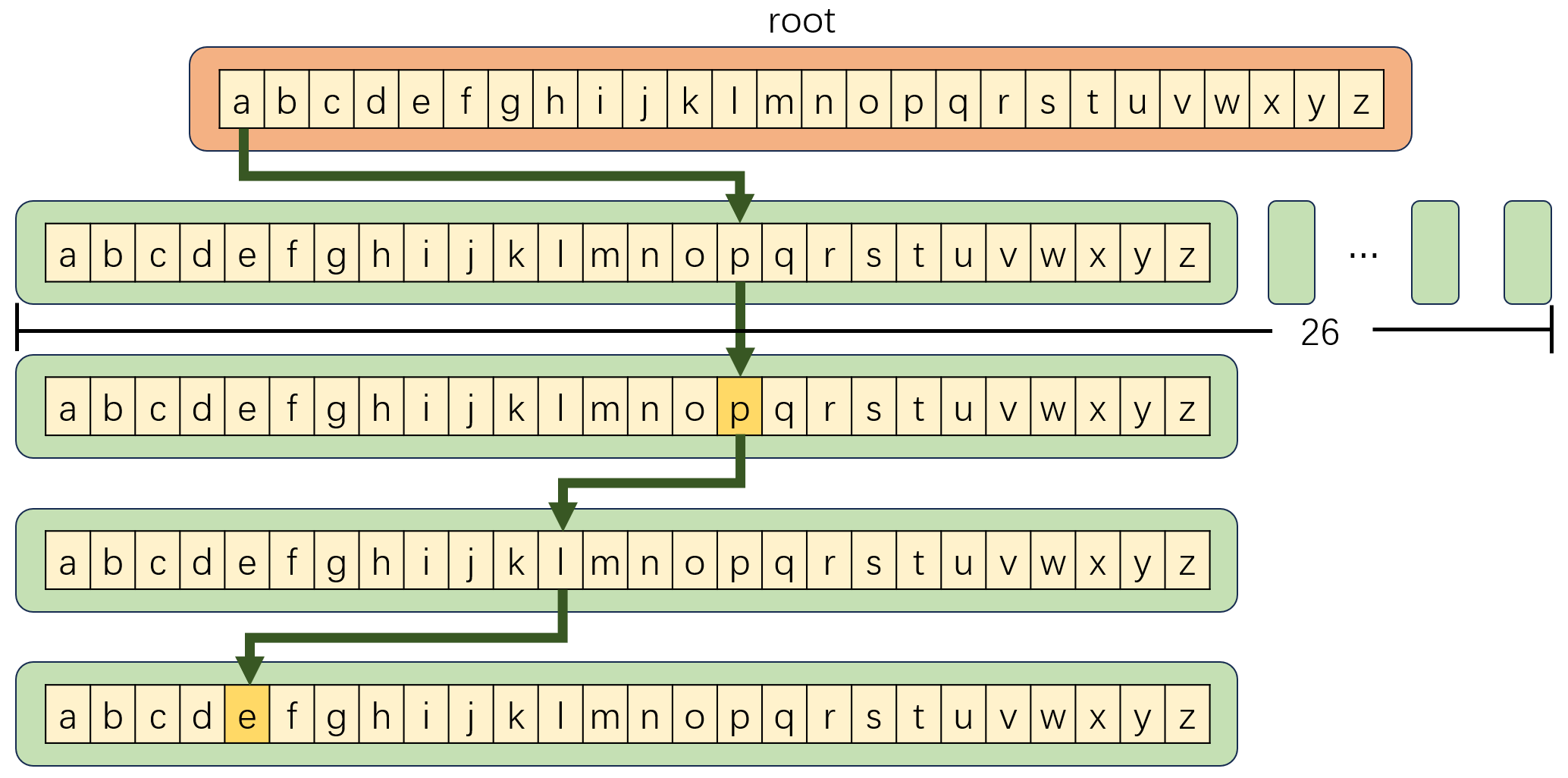
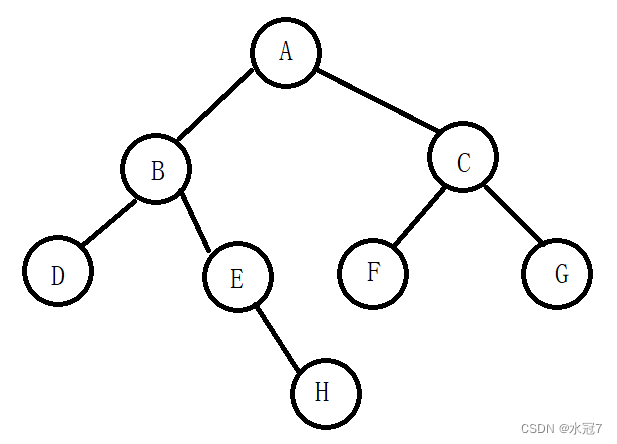
第四题. B树和B+树的区别
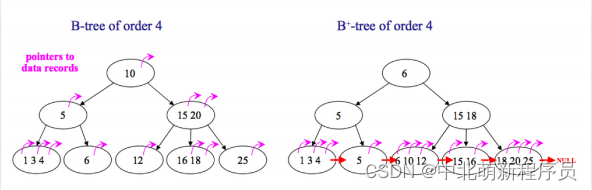
- 在B树中,你可以将键和值存放在内部节点和叶子节点;但在B+树中,内部节点都是键,没有值,叶子节点同时存放键和值。
- B+树的叶子节点有一条链相连,而B树的叶子节点各自独立。
第五题. 使用B树和B+树好处
使用B树的好处
B树可以在内部节点同时存储键和值,因此,把频繁访问的数据放在靠近根节点的地方将会大大提高热点数据的查询效率。这种特性使得B树在特定数据重复多次查询的场景中更加高效。
使用B+树的好处
由于B+树的内部节点只存放键,不存放值,因此,一次读取,可以在内存页中获取更多的键,有利于更快地缩小查找范围。 B+树的叶节点由一条链相连,因此,当需要进行一次全数据遍历的时候,B+树只需要使用O(logN)时间找到最小的一个节点,然后通过链进行O(N)的顺序遍历即可。而B树则需要对树的每一层进行遍历,这会需要更多的内存置换次数,因此也就需要花费更多的时间
如果我的内容对你有帮助,请点赞,评论,收藏。创作不易,大家的支持就是我坚持下去的动力