目录

1  前缀树

1.1  什么是前缀树

1.2  如何构建前缀树

2  208. 实现 Trie（前缀树）

---

菜鸟做题，语言是 C++

1  前缀树

1.1  什么是前缀树

前缀树，也被称作字典树（Trie）或者键树，是一种用于检索字符串数据集中的键的树形数据结构。在前缀树中，每一个节点都代表着一个字符，而路径则代表着字符串。这种数据结构特别适用于自动补全、拼写检查以及自然语言处理等场景。

1.2  如何构建前缀树

根据前缀树的定义，其节点的结构应该为：

class Trie {
private:
    vector<Trie *> children;
    bool isEnd;
}

• 一个 Trie 节点表示一个字母
• children 用于存储下一个字母的 26 种可能
• isEnd 用于表示当前字母是否为某个单词的结尾

这里我们将前缀树定义为 Trie 类而不是 Trie 结构体，是因为它还将提供一些方法。

假设我们需要存储 apple 和 app 这两个单词，则可以构建如下 Trie：

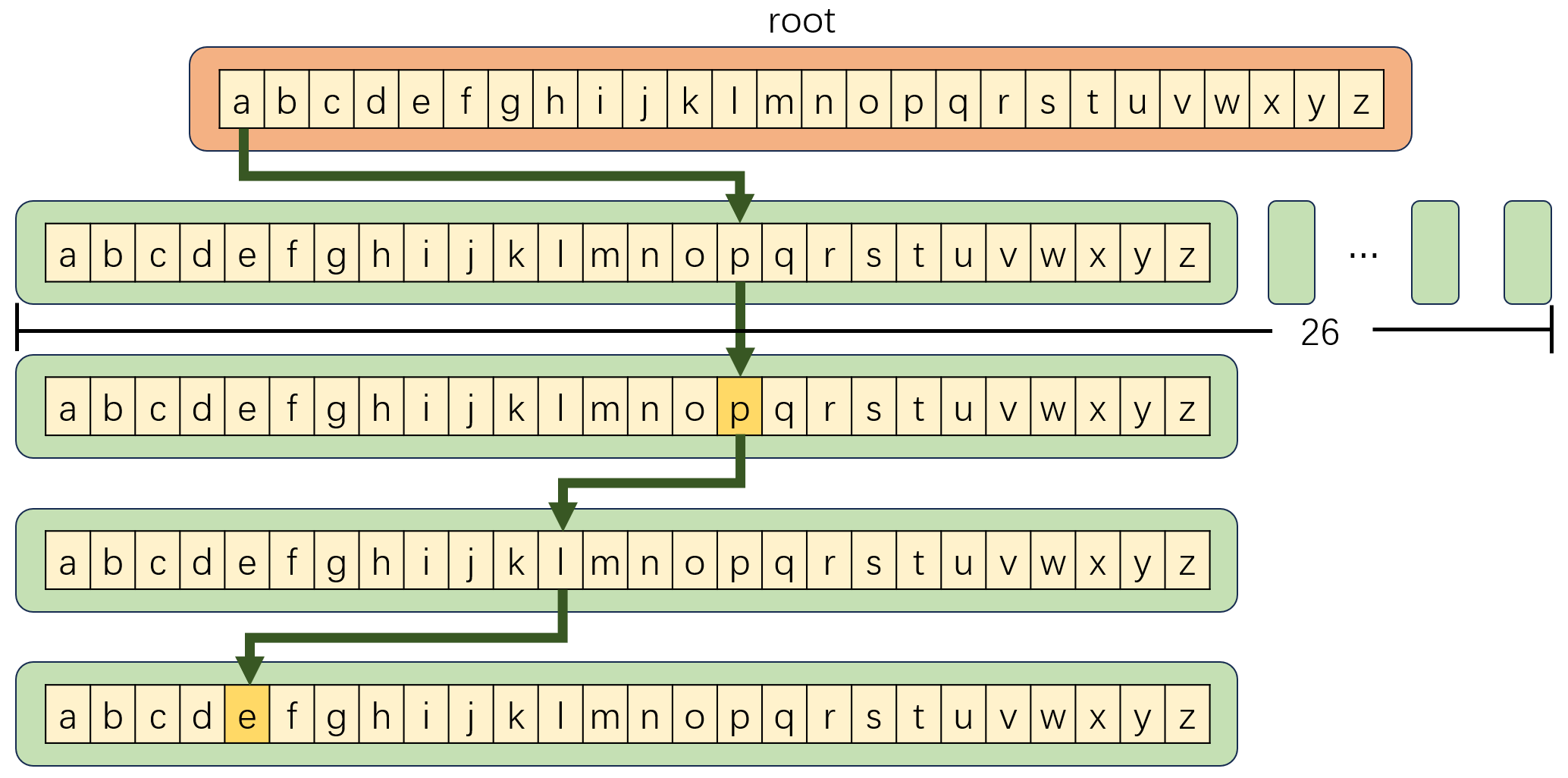
① apple：由于此前还没有种树，因此我们需要创建 root 根节点。接着，因为第一个字母是 a，所以我们为根节点的 children[0] 创建子节点。第二个字母是 p，所以我们为子节点的 children[15] 创建子节点。以此类推。直到字母 e，我们只需要将它所对应的子节点的 isEnd 置为 True 即可。

② app：我们可以直接从 root 根节点开始查询。针对第一个字母 a，由于根节点的 children[0] 已经有子节点了，因此我们直接去找子节点。针对第二个字母 p，由于子节点的 children[15] 已经有子节点了，因此我们直接去找子节点。以此类推。直到最后一个字母 p，我们只需要将它所对应的子节点的 isEnd 置为 True 即可。

图中的 26 表示，children 容器中的每个节点（字母）都可以拥有自己的子节点（字母）。

2  208. 实现 Trie（前缀树）

① 初始化节点：

Trie() : children(26), isEnd(false) {}

② 插入新的字符串：

void insert(string word) {
    Trie * node = this;
    for (auto & ch : word) {
        ch -= 'a';
        if (node->children[ch] == nullptr)
            node->children[ch] = new Trie();
        node = node->children[ch];
    }
    node->isEnd = true;
}
    

this 指针指向的是当前的 Trie 对象，即第一个被创建的节点，也就是根节点。

③ 查询字符串：

bool search(string word) {
    Trie * node = this;
    for (auto & ch : word) {
        ch -= 'a';
        if (node->children[ch] == nullptr)
            return false;
        node = node->children[ch];
    }
    if (node->isEnd) return true;
    return false;
}

④ 查询字符串前缀：

bool startsWith(string prefix) {
    Trie * node = this;
    for (auto & ch : prefix) {
        ch -= 'a';
        if (node->children[ch] == nullptr)
            return false;
        node = node->children[ch];
    }
    return true;
}

和 “查询字符串” 几乎没有区别，只是不要求最后一个字母是某字符串的结尾。

class Trie {
private:
    vector<Trie *> children;
    bool isEnd;

public:
    Trie() : children(26), isEnd(false) {}
    
    void insert(string word) {
        Trie * node = this;
        for (auto & ch : word) {
            ch -= 'a';
            if (node->children[ch] == nullptr)
                node->children[ch] = new Trie();
            node = node->children[ch];
        }
        node->isEnd = true;
    }
    
    bool search(string word) {
        Trie * node = this;
        for (auto & ch : word) {
            ch -= 'a';
            if (node->children[ch] == nullptr)
                return false;
            node = node->children[ch];
        }
        if (node->isEnd) return true;
        return false;
    }
    
    bool startsWith(string prefix) {
        Trie * node = this;
        for (auto & ch : prefix) {
            ch -= 'a';
            if (node->children[ch] == nullptr)
                return false;
            node = node->children[ch];
        }
        return true;
    }
};