离散系统的冲激响应和阶跃响应
求解 H ( z ) = 0.1321 − 0.3963 z − 2 + 0.3963 z − 4 − 0.1321 z − 6 1 + 0.34319 z − 2 + 0.60439 z − 4 + 0.20407 z − 6 H(z)=\frac{0.1321-0.3963z^{-2}+0.3963z^{-4}-0.1321z^{-6}}{1+0.34319z^{-2}+0.60439z^{-4}+0.20407z^{-6}} H(z)=1+0.34319z−2+0.60439z−4+0.20407z−60.1321−0.3963z−2+0.3963z−4−0.1321z−6
初始状态: y ( − 1 ) = 7 , x ( − 1 ) = − 3 y(-1)=7 ,x(-1)=-3 y(−1)=7,x(−1)=−3
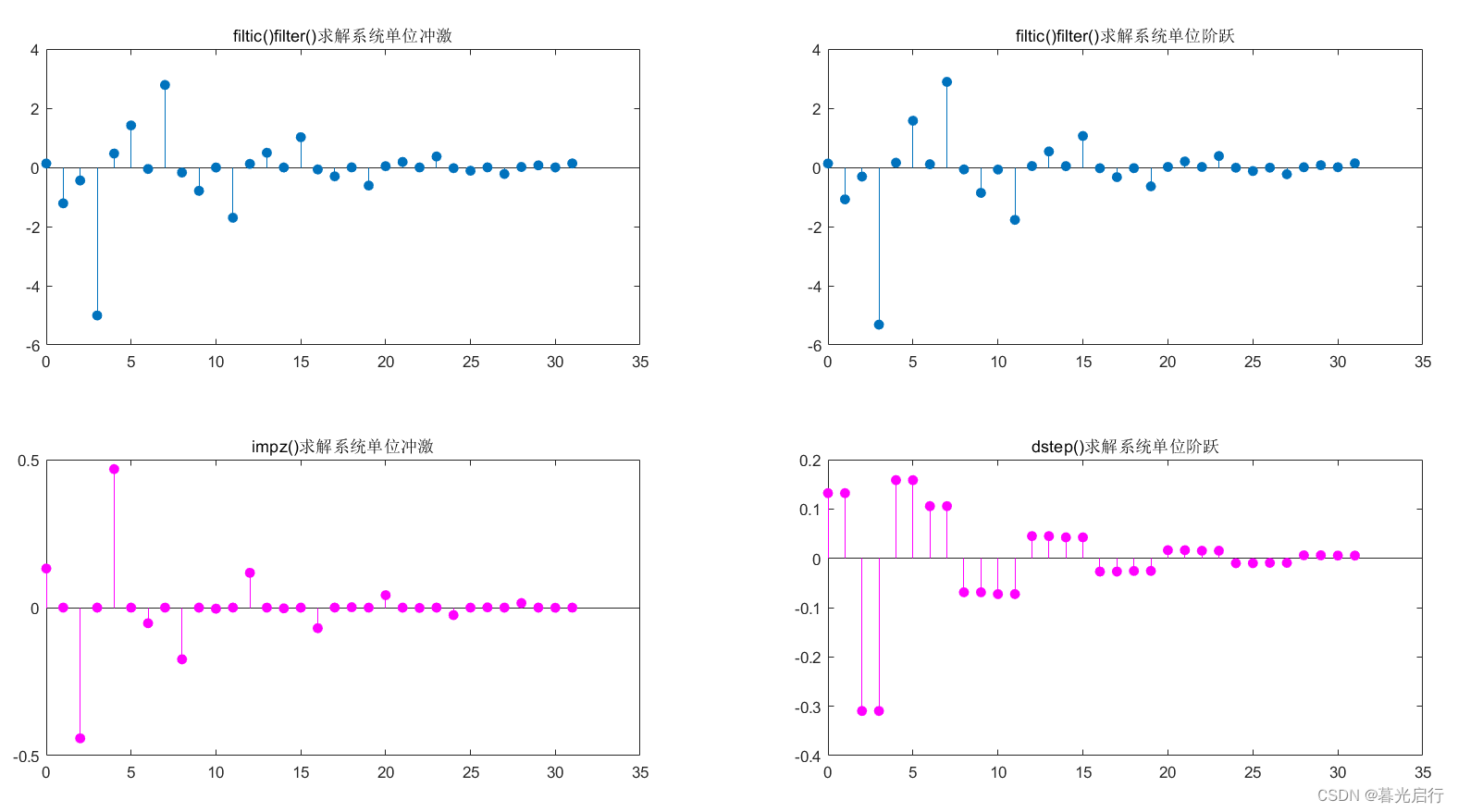
方法一: 使用 impz()dstep() 求冲激和阶跃响应 \textbf{方法一:}使用\textbf{impz()}\textbf{dstep()}求冲激和阶跃响应 方法一:使用impz()dstep()求冲激和阶跃响应
注意只能求解无初始状态的
%% impz()求离散系统单位冲激响应,dstep()求离散系统单位阶跃响应
b = [0.1321 0 -0.3963 0 0.3963 0 -0.1321];
a = [1 0 0.34319 0 0.60439 0 0.20407];
N = 32;
n = 0:N-1;
h = impz(b,a,n);
g = dstep(b,a,n);
figure("color",'w');
subplot(121)
stem(n,h,"filled");title('impz()求解系统单位冲激');
subplot(122)
stem(n,g,"filled");title('dstep()求解系统单位阶跃');
方法二: 使用 filtic()filter() 求冲激和阶跃响应 \textbf{方法二:}使用\textbf{filtic()}\textbf{filter()}求冲激和阶跃响应 方法二:使用filtic()filter()求冲激和阶跃响应
可以求解有初始状态的
%% filtic()和filter()求解离散系统单位冲激响应
clear;
b = [0.1321 0 -0.3963 0 0.3963 0 -0.1321];
a = [1 0 0.34319 0 0.60439 0 0.20407];
N = 32;
n = 0:N-1;
%建立单位冲激信号
x1 = [n==0];
%建立单位阶跃信号
x2 = [n>=0];
x01 = -3;y01 = 7;%初始条件:x(-1)=0,y(-1)=0
xi = filtic(b,a,y01,x01);
h = filter(b,a,x1,xi);
g = filter(b,a,x2,xi);
figure("color",'w');
subplot(221)
stem(n,h,"filled");title('filtic()filter()求解系统单位冲激');
subplot(222)
stem(n,g,"filled");title('filtic()filter()求解系统单位阶跃');
h2 = impz(b,a,n);
g2 = dstep(b,a,n);
subplot(223)
stem(n,h2,"filled");title('impz()求解系统单位冲激');
subplot(224)
stem(n,g2,"filled");title('dstep()求解系统单位阶跃');