已知一个平面上的一点P0和法向量n，一条直线上的点L0和方向L,求该直线与该平面的交点P

如下图

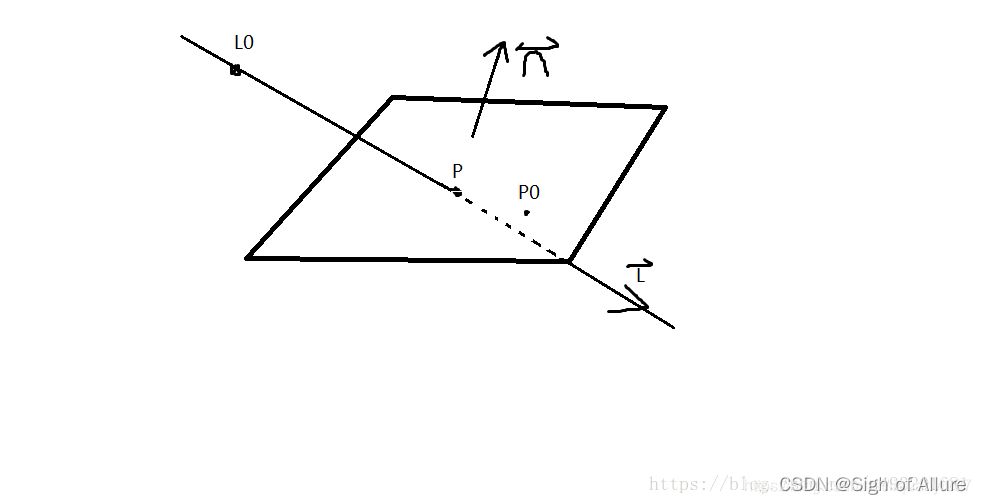
首先我们要知道向量归一化点乘之后得到就是两个向量的夹角的余弦值，如果两个向量相互垂直则值是0，小于0则两个向量的夹角大于90度，大于0则两个向量夹角小于90度，所以可以得出一下公式1：(p-p0)*n=0

而由于交点p是属于直线上的一点，所以我们能推倒出公式2：P=L0+dL;

然后我们把公式2导入到公式1得到：

      (L0+dL-P0)*n=0

      (L0-P0)*n+dL*n=0(点乘满足分配率)

      (p0-L0)*n=dL*n

       d=(p0-L0)*n/L*n(点乘满足结合律)

     只要我们求出d的值带入公式2就能求出交点P.

    /// <summary>
    /// 计算直线与平面的交点
    /// </summary>
    /// <param name="point">直线上某一点</param>
    /// <param name="direct">直线的方向</param>
    /// <param name="planeNormal">垂直于平面的的向量</param>
    /// <param name="planePoint">平面上的任意一点</param>
    /// <returns></returns>
    private bool GetIntersectWithLineAndPlane(Vector3 point, Vector3 direct, Vector3 planeNormal, Vector3 planePoint,out Vector3 result)
    {
        result = Vector3.zero; 
        //要注意直线和平面平行的情况
        float d1 = Vector3.Dot(direct.normalized, planeNormal);
        if(d1 == 0)return false;
        float d2 = Vector3.Dot(planePoint - point, planeNormal);
        float d3 = d2 / d1;
 
        result = d3 * direct.normalized + point;
        return true;
    }