操作环境:
MATLAB 2022a
1、算法描述
OFDM(Orthogonal Frequency Division Multiplexing,正交频分复用)是一种高效的无线信号传输技术,广泛应用于现代通信系统,如Wi-Fi、LTE和5G。OFDM通过将宽带信道划分为多个正交的窄带子载波来传输数据,有效地提高了频谱利用率并降低了多径传播引起的干扰。接下来,我们将详细讨论OFDM系统的关键组成部分,包括导频、训练符号、调制方式、信道估计方法等。
导频与训练符号
在OFDM系统中,导频信号是预先定义的已知信号,用于辅助接收端进行信道估计和同步。它们在频域中被插入到特定的子载波上。根据导频的排布,可以分为两种主要类型:块状导频和梳状导频。
- 块状导频:这种导频布局方式是将导频信号集中放置在某几个OFDM符号中。这种方式简化了信道估计的过程,适合于信道变化不大的场景。
- 梳状导频:在这种布局中,导频被均匀地分散在所有OFDM符号中,每个符号中的几个子载波被用作导频。这种方式更适合于快速变化的信道环境,因为它能提供更连续的信道状态信息。
训练符号是另一种预定义的信号,通常在通信开始时发送,用于辅助接收器进行信道估计、时间同步和频率同步等初始化过程。
调制方式
OFDM系统支持多种调制方式,如QPSK(Quadrature Phase Shift Keying,四相位移键控)、16-QAM(Quadrature Amplitude Modulation,16进制正交幅度调制)、64-QAM等。这些调制方式在每个子载波上独立使用,根据信道条件动态调整,以达到最优的数据传输速率和可靠性。
信道估计方法
信道估计是OFDM系统中的一个核心环节,它的目的是估计出信道对信号的影响,以便于在接收端进行相应的信号恢复。主要的信道估计方法包括:
- LS(Least Squares,最小二乘法):这是最基本的信道估计方法,通过最小化接收到的导频信号与已知导频信号之间的差异来估计信道。它的实现简单,但对噪声敏感。
- MMSE(Minimum Mean Square Error,最小均方误差):相比LS,MMSE在估计过程中考虑了噪声的影响,能够提供更准确的信道估计,但计算复杂度更高。
- SVD(Singular Value Decomposition,奇异值分解):这是一种更高级的信道估计方法,通过对接收信号矩阵进行奇异值分解,提取信道信息。SVD可以提供优秀的性能,但其计算复杂度较高,通常用于对性能要求较高的场景。
结论
OFDM系统通过其独特的多载波技术和正交性原理,有效地解决了无线通信中的多径干扰问题,提高了频谱效率。通过使用导频和训练符号进行精确的信道估计,结合灵活的调制方式,OFDM能够适应各种复杂的通信环境,为现代通信系统提供了一种高效、可靠的解决方案。随着通信技术的不断进步,OFDM及其相关技术的优化和改进仍将是未来研究的重点。
2、仿真结果演示
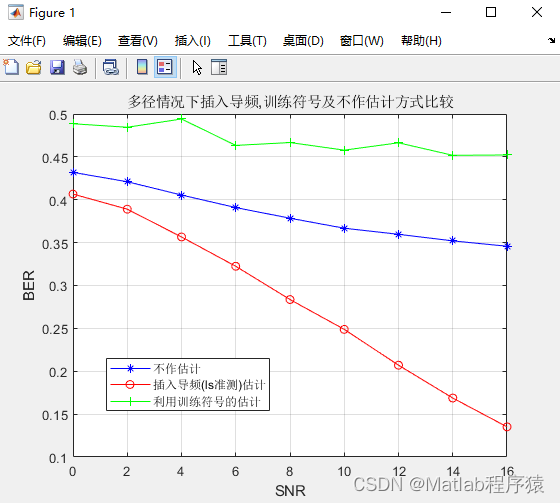
3、关键代码展示
略
4、MATLAB 源码获取
V
点击下方名片