1.1.2 线性规划问题-图解法
- 一、图解法求解步骤(只适用于两个决策变量问题)
- 二、图解法作图实例
- 三、图解法分析线性规划几种解的情况
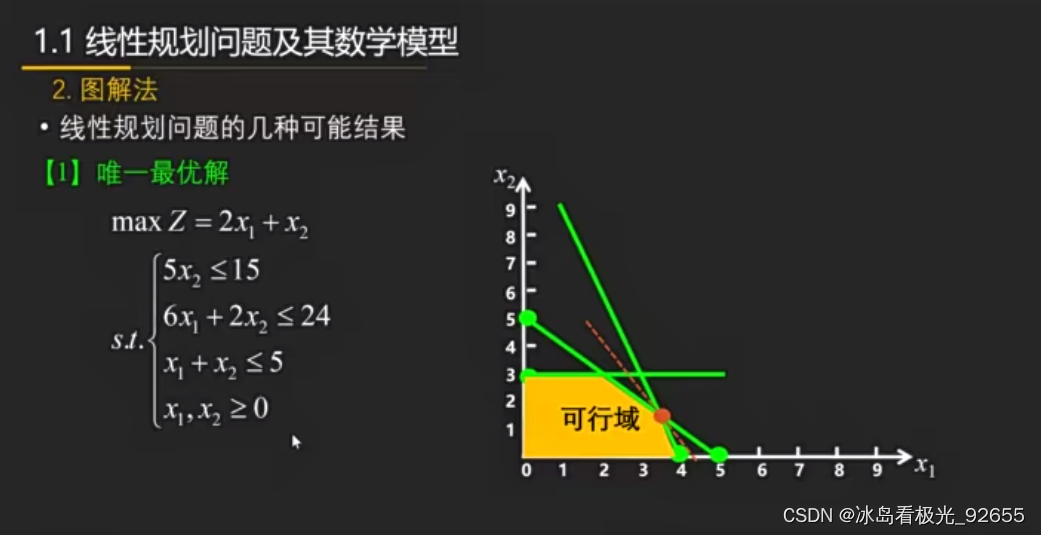
- 1、唯一最优解
- 2、无穷多最优解
- 3、无界解
- 4、无解或无可行解
- 四、图解法的几点启示
一、图解法求解步骤(只适用于两个决策变量问题)
三步走
1、全部约束条件 取等 作图求出可行域
2、做目标函数等值线,确定使目标函数最优化的移动方向
3、平移目标函数等值线,找出最优点,算出最优值。

二、图解法作图实例

三、图解法分析线性规划几种解的情况
1、唯一最优解
2、无穷多最优解

3、无界解
实际问题中约束条件不足 导致 可行域为无界域

4、无解或无可行解
约束条件矛盾导致 可行域为空集
四、图解法的几点启示

结论:
1、线性规划解的情况有:唯一最优解、无穷多最优解、无界解、无可行解
2、若线性规划的可行域存在,则可行域一定是个凸集
3、若线性规划的最优解存在,则最优解或最优解之一(无穷多解时)一定是可行域的凸集的某个顶点
4、解题思路:找出凸集的顶点,计算其目标函数值,比较即得