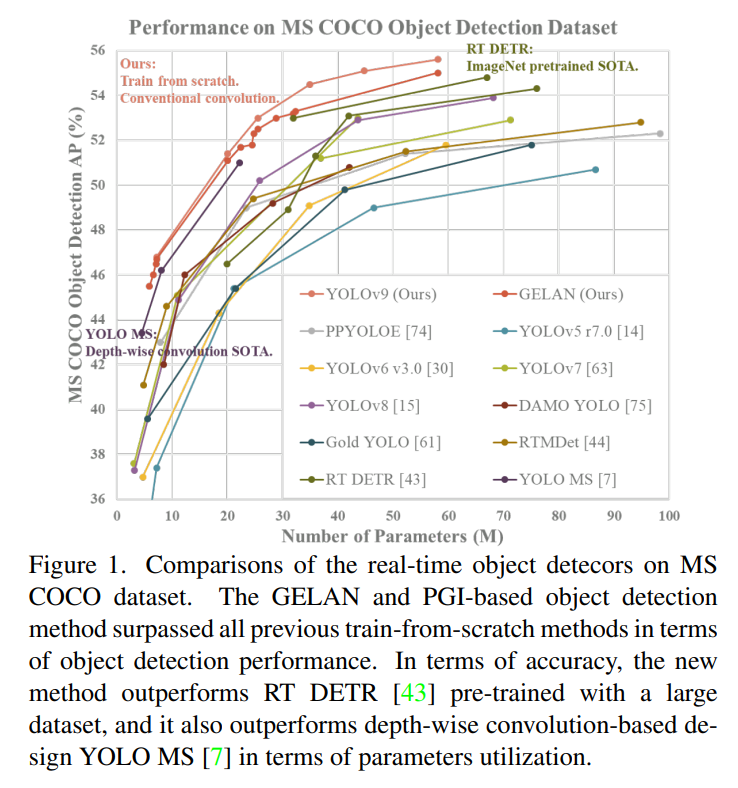
Every day a Leetcode
题目来源:2673. 使二叉树所有路径值相等的最小代价
解法1:遍历
对于满二叉树,父节点 cost[i] 的左右儿子节点分别为 cost[2 * i - 1]、cost[2 * i]。
考虑根到两个互为兄弟节点(父节点相同)的叶子的两条路径。
由于这两条路径除了叶子节点不一样,其余节点都一样,所以为了让这两条路径的路径和相等,必须修改叶子节点的值。
每次操作,你可以将树中任意节点的值增加 1。为了最小化操作次数,我们应该将较小节点值增大到较大节点值。
从最后一个非叶节点开始算,直到根节点之前,遍历这些节点,其左右儿子节点的值分别为 leftSonVal 和 rightSonVal,最小操作次数 min_increase += abs(leftSonVal - rightSonVal),累加路径和,更新 cost[i - 1] += max(leftSonVal, rightSonVal)。
最后返回 min_increase。
代码:
/*
* @lc app=leetcode.cn id=2673 lang=cpp
*
* [2673] 使二叉树所有路径值相等的最小代价
*/
// @lc code=start
class Solution
{
public:
int minIncrements(int n, vector<int> &cost)
{
int min_increase = 0;
// 从最后一个非叶节点开始算
for (int i = n / 2; i > 0; i--)
{
int leftSonVal = cost[2 * i - 1];
int rightSonVal = cost[2 * i];
// 两个子节点变成一样的,值为较大者
min_increase += abs(leftSonVal - rightSonVal);
// 累加路径和
cost[i - 1] += max(leftSonVal, rightSonVal);
}
return min_increase;
}
};
// @lc code=end
结果:
复杂度分析:
时间复杂度:O(n),其中 n 为数组 cost 的长度。
空间复杂度:O(1)。
解法2:递归
代码:
class Solution
{
public:
int minIncrements(int n, vector<int> &cost)
{
int min_increase = 0;
function<int(int)> dfs = [&](int index) -> int
{
if (2 * index > n)
return cost[index - 1];
int leftSonVal = dfs(2 * index);
int rightSonVal = dfs(2 * index + 1);
min_increase += abs(leftSonVal - rightSonVal);
return max(leftSonVal, rightSonVal) + cost[index - 1];
};
dfs(1);
return min_increase;
}
};
结果:

复杂度分析:
时间复杂度:O(n),其中 n 为数组 cost 的长度。
空间复杂度:O(logn),其中 n 为数组 cost 的长度。