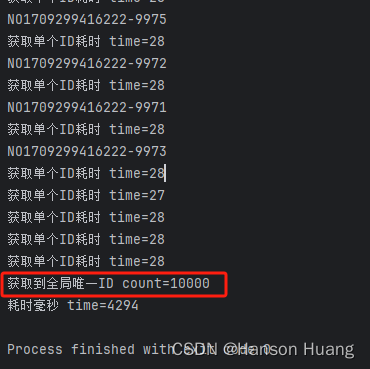
方阵
行与列数量相等的矩阵,n*n阶矩阵
对角矩阵
当对角线以外的矩阵内元素全为0,则称之为对角矩阵,对角矩阵的前提是必须是方阵
单位矩阵
对角线元素全为1,其余元素全为0,属于对角矩阵的一部分
矩阵和向量
把1 * n阶矩阵称为行向量,n * 1阶矩阵称为列向量
当向量与矩阵进行运算的时候需要确定是行向量还是列向量
矩阵的转置
[
1
2
3
4
5
6
7
8
9
]
T
\begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{bmatrix} ^T
147258369
T =
[
1
4
7
2
5
8
3
6
9
]
\begin{bmatrix} 1 & 4 & 7\\ 2 & 5 & 8\\ 3 & 6 & 9 \end{bmatrix}
123456789
即行变为列,列变为行
矩阵转置的转置是其本身
对角矩阵的转置是其本身
标量与矩阵的乘法
以三阶矩阵为例:
kM = k [ m 11 m 12 m 13 m 21 m 22 m 23 m 31 m 32 m 33 ] \begin{bmatrix} m_{11} & m_{12} & m_{13}\\ m_{21} & m_{22} & m_{23}\\ m_{31} & m_{32} & m_{33} \end{bmatrix} m11m21m31m12m22m32m13m23m33 = [ k m 11 k m 12 k m 13 k m 21 k m 22 k m 23 k m 31 k m 32 k m 33 ] \begin{bmatrix} km_{11} & km_{12} & km_{13}\\ km_{21} & km_{22} & km_{23}\\ km_{31} & km_{32} & km_{33} \end{bmatrix} km11km21km31km12km22km32km13km23km33
矩阵的乘法
相乘的条件:前一个矩阵的列等于下一个矩阵的行

矩阵乘法特点

向量矩阵相乘

DX中是行向量
OpenGL中是列向量