一、题目
1、题目描述
经过重重笔试面试的考验,小明成功进入 Macrohard 公司工作。
今天小明的任务是填满这么一张表:
表有 �n 行 �n 列,行和列的编号都从 11 算起。
其中第 �i 行第 �j 个元素的值是 gcd(�,�)gcd(i,j) 的平方,gcdgcd 表示最大公约数,以下是这个表的前四行的前四列:
1 1 1 1 1 4 1 4 1 1 9 1 1 4 1 16小明突然冒出一个奇怪的想法,他想知道这张表中所有元素的和。 由于表过于庞大,他希望借助计算机的力量。
2、输入输出
2.1输入
一行一个正整数 �n 意义见题。
2.2输出
一行一个数,表示所有元素的和。由于答案比较大,请输出模 10000000071000000007(即109+7109+7)后的结果。
3、原题链接
P8670 [蓝桥杯 2018 国 B] 矩阵求和 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
二、解题报告
1、思路分析
先对公式进行化简
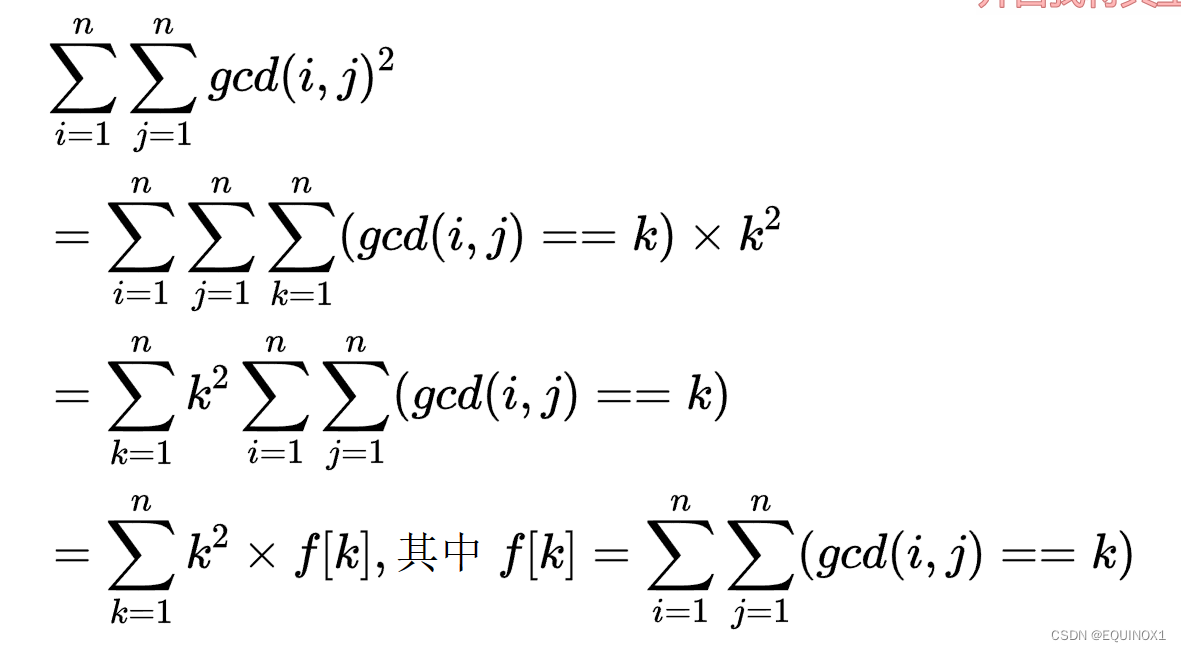
我们外层枚举需要O(n)的时间复杂度,那么对于f[k]的计算有没有快速的方法?
1 1 1 1
1 4 1 4
1 1 9 1
1 4 1 16以示例为例,我们先考虑以2为公因数(注意并非gcd)的(i,j)数,显然有[4 / 2] * [4 / 2] = 4个
而此时矩阵中有3个2,原因是第四个2被16替代了,因为4作为比2大的数是(4,4)的gcd
因此我们可以得出以k为gcd的(i,j)数为[n / k] * [n/ k] - f[j](j为k的倍数)
这样就得到了f[]的转移方程,这个状态转移是O(lnn)的
注意写代码时若干运算的选择,很可能因为多进行一次取模而导致没过
nlnn对于1e7数据量而言还是有点慢
2、复杂度
时间复杂度: O(nlnn)空间复杂度:O(n)
3、代码详解
#include <iostream>
#include <cstring>
using namespace std;
#define int long long
const int N = 1e7 + 10, mod = 1e9 + 7;
int n, f[N], res = 0;
void solve()
{
cin >> n;
for (int i = n; i >= 1; i--)
{
f[i] = ((n / i) * (n / i)) % mod;
for (int j = i << 1; j <= n; j += i)
f[i] = (f[i] - f[j] + mod) % mod;
res = (res + f[i] * (i * i) % mod) % mod;
}
cout << res;
}
signed main()
{
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
//freopen("in.txt", "r", stdin);
int _ = 1;
while (_--)
solve();
return 0;
}