C++数据结构与算法——二叉树的属性

news2024/9/22 3:36:58

C++第二阶段——数据结构和算法，之前学过一点点数据结构，当时是基于Python来学习的，现在基于C++查漏补缺，尤其是树的部分。这一部分计划一个月，主要利用代码随想录来学习，刷题使用力扣网站，不定时更新，欢迎关注！

文章目录

  • 一、对称二叉树（力扣101）
  • 二、二叉树的最大深度（力扣104）
  • 三、二叉树的最小深度（力扣111）
  • 四、完全二叉树的节点个数（力扣222）
  • 五、平衡二叉树（力扣110）
  • 六、二叉树的所有路径（力扣257）
  • 七、左叶子之和（力扣404）
  • 八、找树左下角的值（513）
  • 九、路径总和（力扣112）

一、对称二叉树（力扣101）

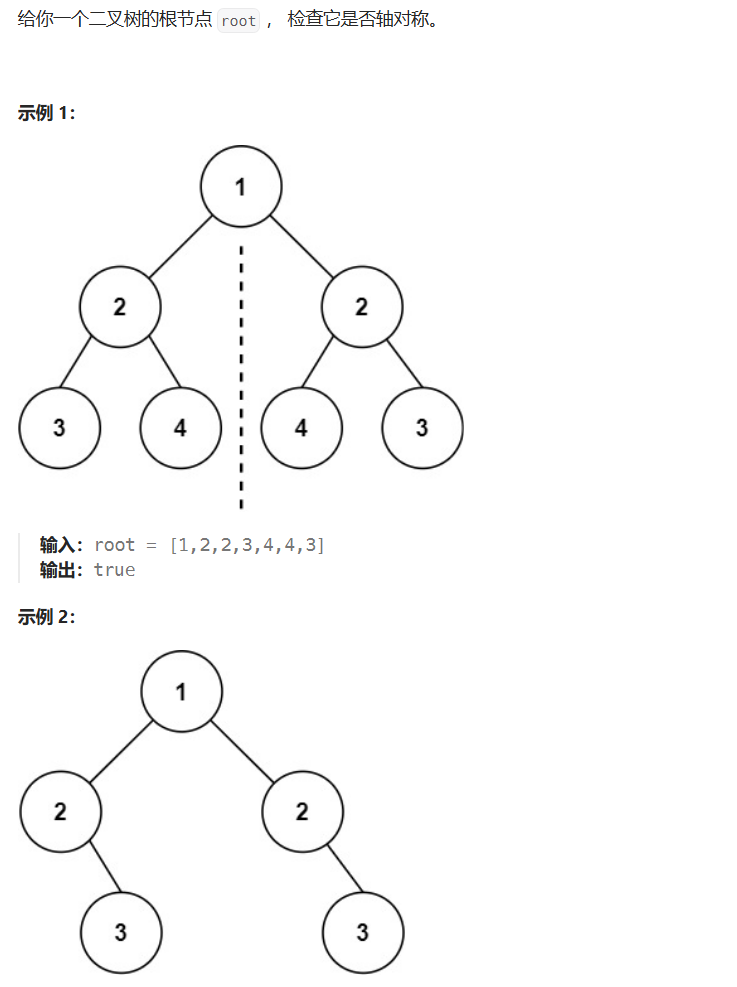
在这里插入图片描述

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if(root==NULL) return root;
        return isSymmetricLeftRight(root->left,root->right);
    }
    bool isSymmetricLeftRight(TreeNode* left,TreeNode* right){
        if(left==NULL&&right==NULL) return true;
        else if(left==NULL&&right!=NULL) return false;
        else if(left!=NULL&&right==NULL) return false;
        else if(left->val!=right->val) return false;
        else{
            bool outside = isSymmetricLeftRight(left->left,right->right);
            bool inside = isSymmetricLeftRight(left->right,right->left);
            if(outside!=true||inside!=true){
                return false;
            }
        }
        return true;
    }
};

在这里插入图片描述

二、二叉树的最大深度（力扣104）

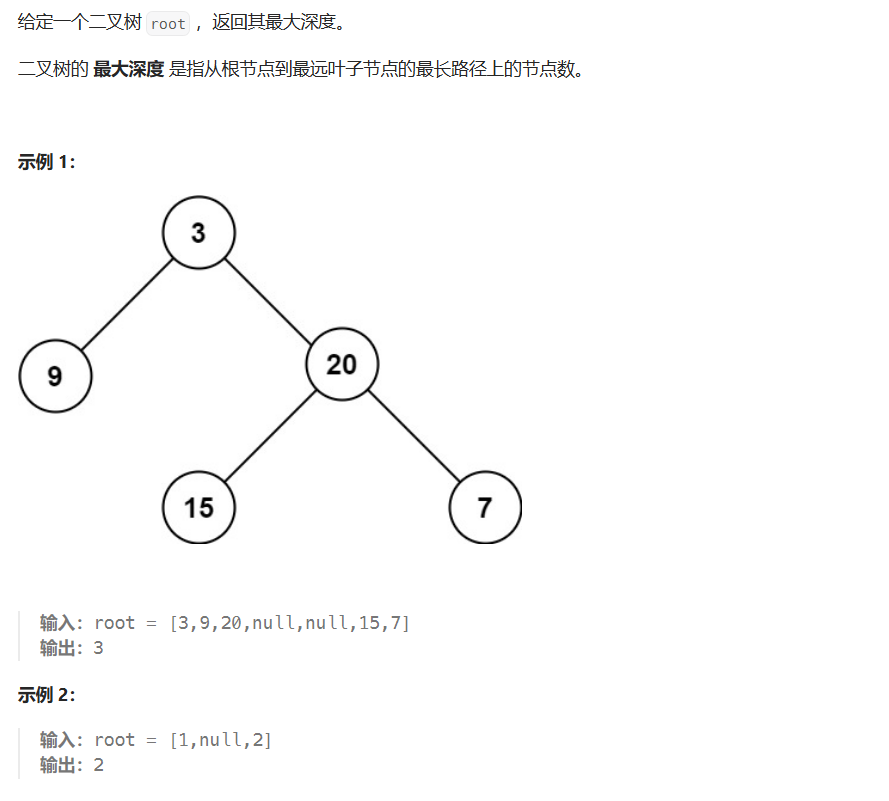
在这里插入图片描述

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root==NULL) return 0;
        int leftDepth = maxDepth(root->left);
        int rightDepth = maxDepth(root->right);
        int result = 1+max(leftDepth,rightDepth);
        return result;
    }
};

在这里插入图片描述

三、二叉树的最小深度（力扣111）

在这里插入图片描述

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minDepth(TreeNode* root) {
        if(root==NULL) return 0;
        int leftDepth = minDepth(root->left);
        int rightDepth = minDepth(root->right);
        if (root->left == NULL && root->right != NULL) { 
            return 1 + rightDepth;
        }   
        // 当一个右子树为空，左不为空，这时并不是最低点
        if (root->left != NULL && root->right == NULL) { 
            return 1 + leftDepth;
        }
        return min(leftDepth,rightDepth)+1;
    }
};

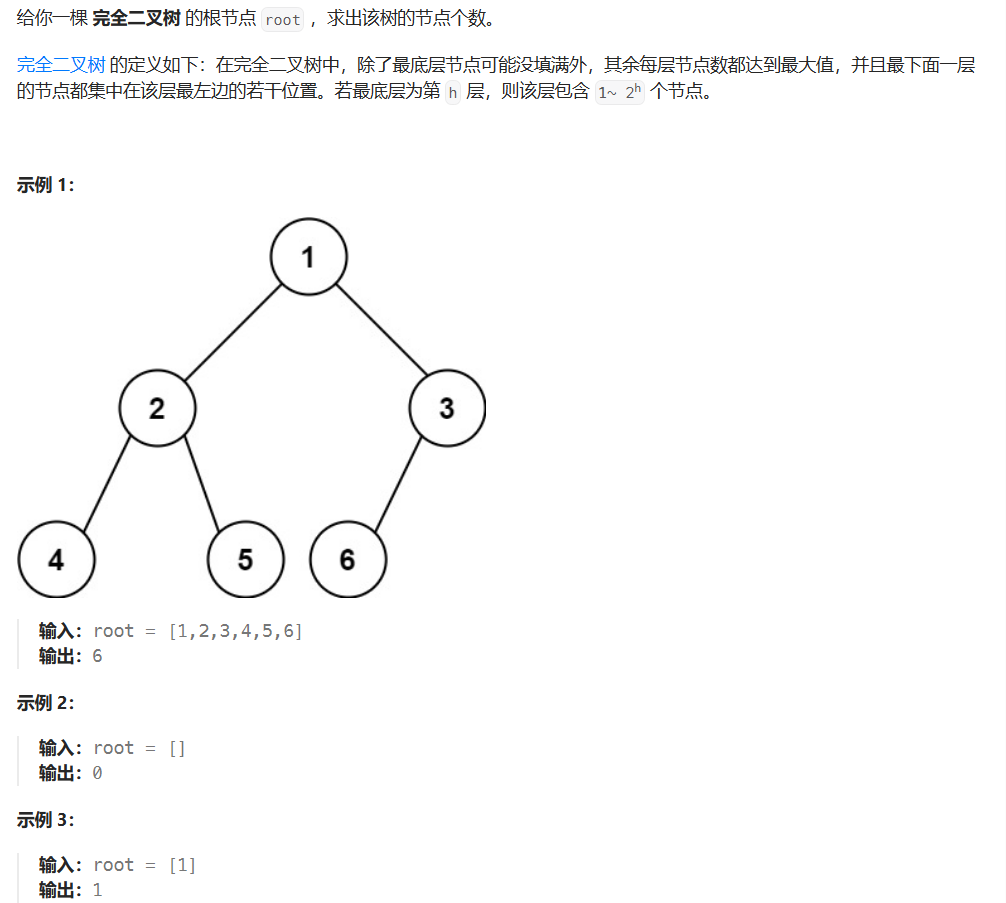
在这里插入图片描述

四、完全二叉树的节点个数（力扣222）

在这里插入图片描述

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int countNodes(TreeNode* root) {
        int count=0;
        tr(root,count);
        return count;
    }
    void tr(TreeNode* root,int &count){
        if(root==NULL) return;
        tr(root->left,count);
        tr(root->right,count);
        count++;
    }
};

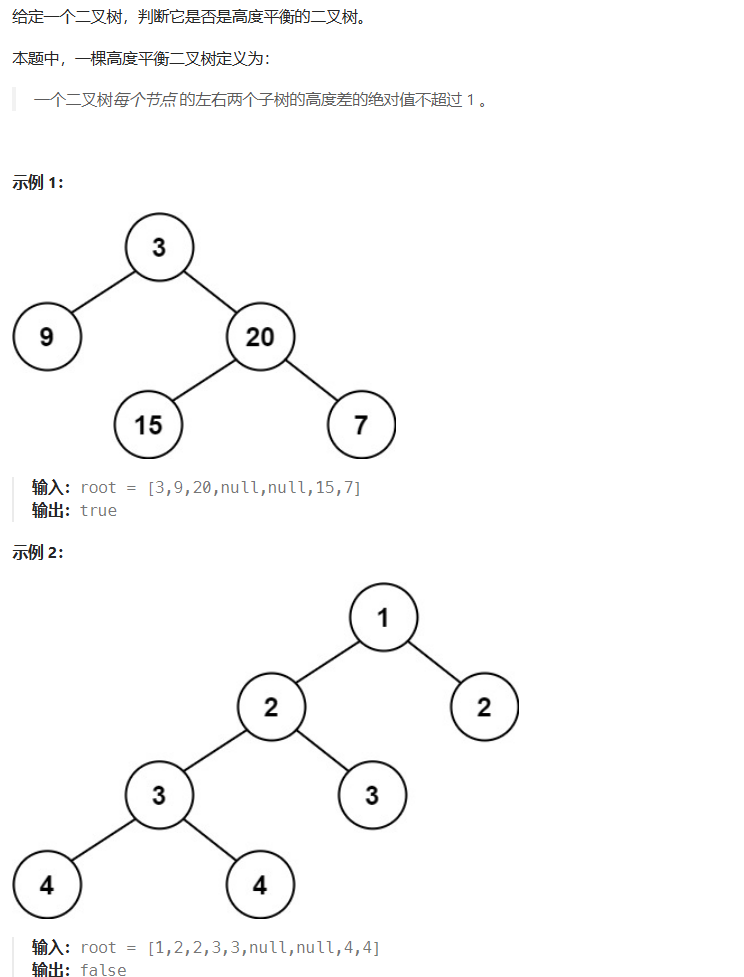
在这里插入图片描述

五、平衡二叉树（力扣110）

在这里插入图片描述

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isBalanced(TreeNode* root) {
        if(root==NULL) return true;
        int result = getLength(root);
        if(result==-1) return false;
        return true;
    }
    int getLength(TreeNode* root){
        if(root==NULL) return 0;
        int leftLength = getLength(root->left);
        if(leftLength==-1) return -1;
        int rightLength = getLength(root->right);
        if(rightLength==-1) return -1;
        int result;
        if(abs(leftLength-rightLength)>1) return -1;
        else{
            result = max(rightLength,leftLength)+1;
        }
        return result;
    }
};

在这里插入图片描述

六、二叉树的所有路径（力扣257）

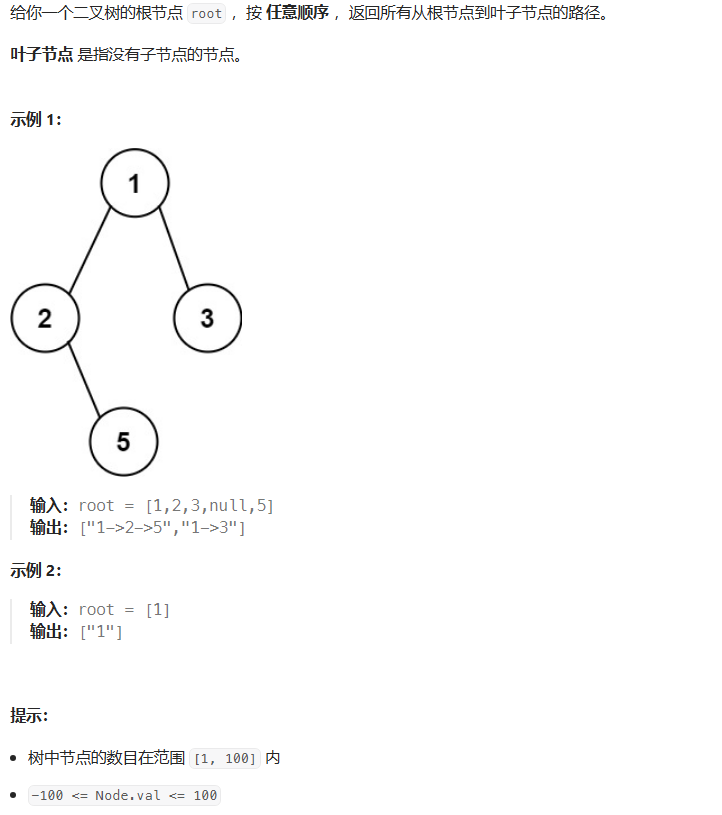
在这里插入图片描述

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> result;
        vector<int> path;
        traversal(root,path,result);
        return result;
    }
    void traversal(TreeNode * root,vector<int>& path,vector<string> &result){
        path.push_back(root->val);
        if(root->left==NULL&&root->right==NULL) {
            string temp;
            for(int i=0;i<path.size();i++){
                if(i==path.size()-1){
                    temp+= to_string(path[i]);
                }
                else{
                    temp+=to_string(path[i]);
                    temp+="->";
                }
            }
            result.push_back(temp);
            return;
        }
        if(root->left){
            traversal(root->left,path,result);
            path.pop_back();
        }
        if(root->right){
            traversal(root->right,path,result);
            path.pop_back();
        }

    }
};

在这里插入图片描述

七、左叶子之和（力扣404）

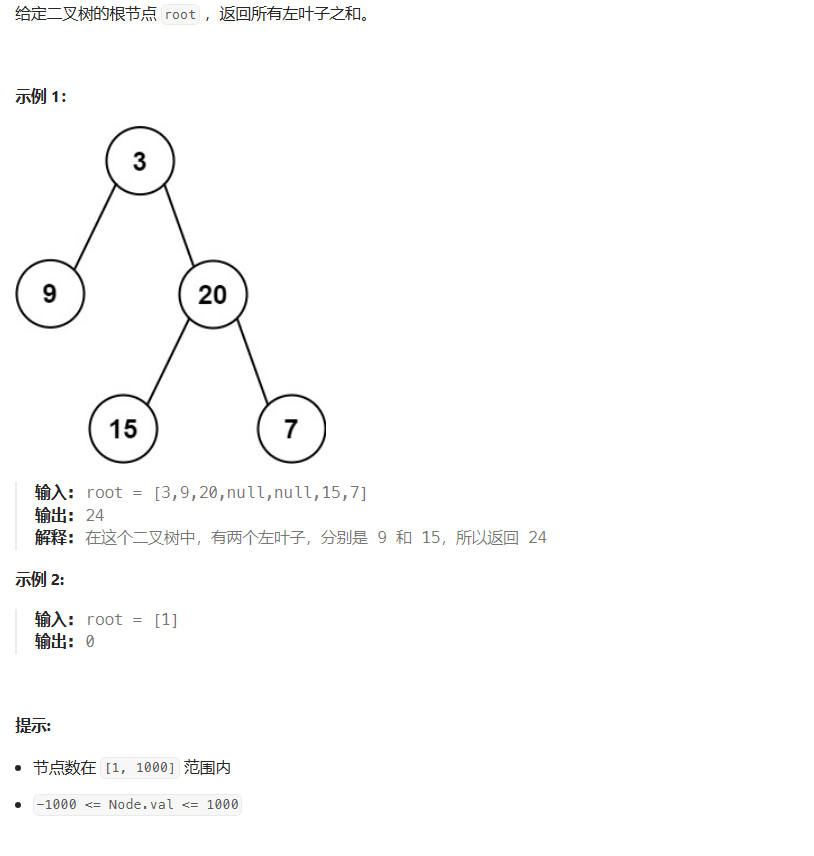
在这里插入图片描述

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int sumOfLeftLeaves(TreeNode* root) {
        int sum=0;
        return trv(root,sum);
    }
    // 后续遍历
    int trv(TreeNode *root,int &sum){
        if(root==NULL) return 0;
        trv(root->left,sum);
        trv(root->right,sum);
        if(root->left!=NULL&&root->left->left==NULL&&root->left->right==NULL){
            sum+= root->left->val;
        }
        return sum;
    }
};

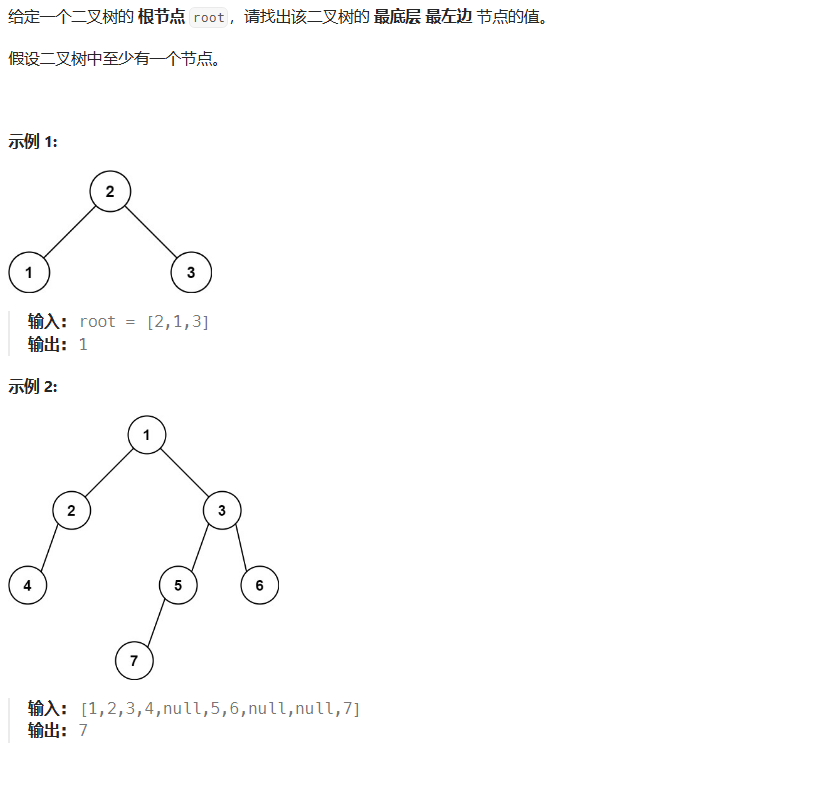
在这里插入图片描述

八、找树左下角的值（513）

在这里插入图片描述

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int findBottomLeftValue(TreeNode* root) {
        vector<vector<int>> result = func(root);
        return result[result.size()-1][0];
    }
    // 层序遍历
    vector<vector<int>> func(TreeNode* root){
        vector<vector<int>> result;
        queue<TreeNode*> que;
        if(root!=NULL) que.push(root);
        while(!que.empty()){
            vector<int> vec;
            int Qsize=que.size();
            while(Qsize--){
                TreeNode * top = que.front();
                que.pop();
                vec.push_back(top->val);
                if(top->left) que.push(top->left);
                if(top->right) que.push(top->right);
            }
            result.push_back(vec);
        }
        return result;
    }
};

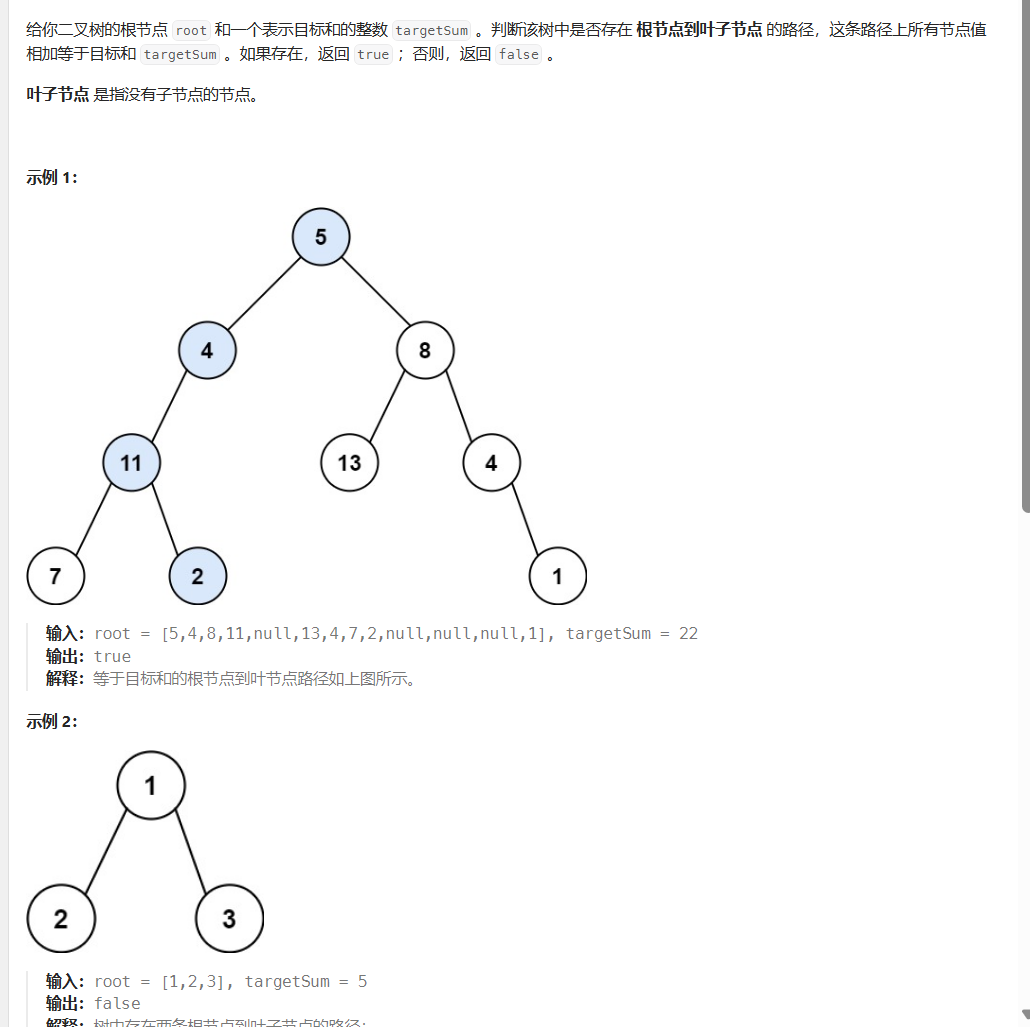
在这里插入图片描述

九、路径总和（力扣112）

在这里插入图片描述

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        vector<int> sumAll;
        vector<int> path;
        if(root==NULL) return false;
        traversal(root,path,sumAll);
        for(int i=0;i<sumAll.size();i++){
            if(sumAll[i]==targetSum){
                return true;
            }
        }
        return false;

    }
    void traversal(TreeNode*root,vector<int> &path,vector<int> &result){
        path.push_back(root->val);
        if(root->left==NULL&&root->right==NULL){
            int sum=0;
            for(int i=0;i<path.size();i++){
                sum+= path[i];
            }
            result.push_back(sum);
        }
        if(root->left) {
            traversal(root->left,path,result);
            path.pop_back();
        }
        if(root->right){
            traversal(root->right,path,result);
            path.pop_back();
        }
    }

};

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1481166.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

C++——String（1）

C++——String（1）

目录 1. 为什么学习string类&#xff1f; 1.1 C语言中的字符串 1.2 相关题目 2. 标准库中的string类 2.1 string类&#xff08;了解一下&#xff09; 2.2 string类的常用接口说明 1. string类对象的常见构造 2. string类对象的容量操作 3. string类对象的访问及遍历操作…
阅读更多...
瑞_Redis_Redis的Java客户端

瑞_Redis_Redis的Java客户端

文章目录 1 Redis的Java客户端1.1 Jedis快速入门1.1.1 入门案例1.1.1.1 项目构建1.1.1.2 引入依赖1.1.1.3 建立连接1.1.1.4 释放资源1.1.1.5 测试1.1.1.6 完整测试类代码 1.1.2 Jedis连接池1.1.2.1 连接池工具类1.1.2.2 改造原始代码 &#x1f64a; 前言&#xff1a;本文章为瑞…
阅读更多...
【Java程序设计】【C00327】基于Springboot的高校教师教研信息填报系统（有论文）

【Java程序设计】【C00327】基于Springboot的高校教师教研信息填报系统（有论文）

基于Springboot的高校教师教研信息填报系统&#xff08;有论文&#xff09; 项目简介项目获取开发环境项目技术运行截图 项目简介 这是一个基于Springboot的高校教师教研信息填报系统&#xff0c;本系统有管理员、教研管理以及教研人员三种角色&#xff1b; 管理员&#xff1a…
阅读更多...
bvh文件，人体骨骼重定向

bvh文件，人体骨骼重定向

关于两个bvh文件&#xff0c;人体骨骼重定向&#xff0c;小白记录 1、打开 Motionbuilder &#xff0c;选择 打开特定路径下的bvh文件。 绑定骨骼&#xff08;在绑定骨骼过程中&#xff0c;如果骨骼角度&#xff0c;大小之类的不方便&#xff0c;可以shift键加鼠标拖拽界面&…
阅读更多...
Fabric V2.5 通用溯源系统——应用后端GIN框架部分设计

Fabric V2.5 通用溯源系统——应用后端GIN框架部分设计

本节对Fabric V2.5 通用溯源系统的应用后端部分做一个简单的介绍，包括目录结构、文件作用、用户注册登录与农产品信息上链过程介绍。此节内容免费发布在TrueTechLabs Fabric学习交流QQ群。 购买专栏前请认真阅读：《Fabric项目学习笔记》专栏介绍 TrueTechLabs Fabric学习交流…
阅读更多...
蓝桥杯刷题2

蓝桥杯刷题2

1. 修建灌木 import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner scan new Scanner(System.in);int n scan.nextInt();for (int i 1;i < n1;i){int distance Math.max(i-1,n-i);System.out.println(distance*2);}scan.close…
阅读更多...
Node.js+Express后端,自定义接口

Node.js+Express后端,自定义接口

6分钟学会Express 后端 API 开发 Node.js 2020最新版_哔哩哔哩_bilibili 要使用Node.js和Express搭建一个简单的后台服务器&#xff0c;用于接收带有token的请求头&#xff0c;你可以按照以下步骤进行操作&#xff1a; 首先&#xff0c;确保你已经安装了Node.js和npm&#xff0…
阅读更多...
马斯克正式起诉OpenAI和奥特曼！

马斯克正式起诉OpenAI和奥特曼！

就在刚刚&#xff0c;马斯克闹出来一件大事——正式起诉OpenAI和Sam Altman&#xff0c;并要求OpenAI 恢复开源GPT-4等模型&#xff01; 众所周知&#xff0c;马斯克这两年一只在推特上指责 OpenAI是CloseAI(不开源)&#xff0c;但都只是停留在口头上。 而这次马斯克动了真格。…
阅读更多...
Qt 自定义长条进度条（类似播放器进度条）

Qt 自定义长条进度条（类似播放器进度条）

1.运行界面 2.步骤 其实很简单。 2.1绘制底图圆角矩形 2.2绘制播放进度圆角矩形 参考&#xff1a;painter绘图 3.源码 #pragma once#include <QWidget> #include <QLabel> #include <QHBoxLayout> #include <QMouseEvent> #include <QDebug&g…
阅读更多...
2D割草/吸血鬼游戏 性能优化——GPU Spine动画

2D割草/吸血鬼游戏 性能优化——GPU Spine动画

视频中万人同屏方案(gpu动画、渲染、索敌、避障等功能)&#xff0c;可某宝搜店铺&#xff1a;【游戏开发资源商店】获取整套方案源码。 在过去的几年里&#xff0c;割草、类吸血鬼玩法的游戏频出爆款&#xff0c;其丰富的技能、满屏特效、刷怪清屏的解压畅快是此类游戏的核心&…
阅读更多...
队列实现栈与栈实现队列

队列实现栈与栈实现队列

文章目录 前言一、使用队列实现栈二、使用栈实现队列 前言 1、用于巩固栈和队列。 2、本章是使用纯C语言实现的栈和队列&#xff0c;不懂的可以先看看这个喔&#xff1a;c语言实现栈和队列&#xff0c;当然这里直接用C的栈和队列会更方便哦。 3、利于复习C语言的知识点。 一、使…
阅读更多...
杭电OJ 2044 一只小蜜蜂... C++

杭电OJ 2044 一只小蜜蜂... C++

思路&#xff1a;本质与斐波那契数列一样&#xff0c;关键在于a与b之差 #include <iostream> #include <vector> using namespace std; int main() { vector<long long> nums(51); nums[0] 0; nums[1] 1; nums[2] 2; for (int i 3; i < 5…
阅读更多...
设计模式——2_3 迭代器（Iterator）

设计模式——2_3 迭代器（Iterator）

生活就像一颗巧克力&#xff0c;你永远不知道下一颗是什么味道 ——《阿甘正传》 文章目录 定义图纸一个例子&#xff1a;假如你的采集器供应商提供了不同类型的返回值单独的遍历流程实现 碎碎念如果读写同时进行会发生啥&#xff1f;外部迭代和内部迭代迭代器和其他模式迭代器…
阅读更多...
Spring框架知识点

Spring框架知识点

Spring框架知识点 Spring框架中的单例Bean是线程安全的吗&#xff1f; 答&#xff1a;Spring框架中有一个Scope注解&#xff0c;默认值是singleton&#xff0c;单例的&#xff0c;当bean中定义了可变参数&#xff0c;就不是线程安全的。我们建议不要注入有状态的变量&#xf…
阅读更多...
备战蓝桥杯Day21 - 堆排序的内置模块+topk问题

备战蓝桥杯Day21 - 堆排序的内置模块+topk问题

一、内置模块 在python中&#xff0c;堆排序已经设置好了内置模块&#xff0c;不想自己写的话可以使用内置模块&#xff0c;真的很方便&#xff0c;但是堆排序算法的底层逻辑最好还是要了解并掌握一下的。 使用heapq模块的heapify()函数将列表转换为堆&#xff0c;然后使用he…
阅读更多...
librtmp源码分析

librtmp源码分析

阅读了librtmp的源码&#xff0c;简单记录下。 首先补充下AMF格式基本知识 1 AMF格式 AMF是Action Message Format(动作消息格式)的简写&#xff0c;它是一种二进制的数据格式。它的设计是为了把actionscript里面的数据(包括Object, Array, Boolean, Number等)序列化成二进制…
阅读更多...
工业现场网络性能评估方案

工业现场网络性能评估方案

最近要去一个工厂排查网络和电脑卡顿的问题,为此&#xff0c;我准备了以下的方案&#xff0c;在现场以抓包和网络监控的方式来排查。 1.评估流程 为了评估Linux系统的网络负荷&#xff0c;并使用tcpdump来捕获数据包进行分析&#xff0c;您需要遵循以下几个步骤&#xff1a; …
阅读更多...
一种基于三角剖分划分白区范围的白平衡算法

一种基于三角剖分划分白区范围的白平衡算法

常规的白平衡算法中，一般会通过标准色温的R/G-B/G建议色温坐标系，然后在该坐标系中设定白区范围，对落入到白区范围的R/G/B进行加权统计处理，输出给到软件进行白平衡的增益计算。 所介绍的这篇专利利用三角剖分的算法，在划定的白区范围内，利用各个标准色温光源下所标定的白…
阅读更多...
深入解析Golang的encoding/ascii85库：从基础到实战

深入解析Golang的encoding/ascii85库：从基础到实战

深入解析Golang的encoding/ascii85库&#xff1a;从基础到实战 引言基础知识什么是ASCII85编码&#xff1f;ASCII85编码的工作原理ASCII85编码的优点ASCII85编码的缺点 使用Golang的encoding/ascii85库引入encoding/ascii85包ASCII85编码ASCII85解码实战示例小结 进阶技巧和最佳…
阅读更多...
经典文献阅读之--CamMap(基于SLAM地图对不共视相机进行外参标定)

经典文献阅读之--CamMap(基于SLAM地图对不共视相机进行外参标定)

0. 简介 由于多相机之间通常存在有限或无重叠的视场&#xff0c;因此在估计外参相机参数时面临着一定的挑战&#xff0c;为了解决这个问题&#xff0c;本文提出了CamMap&#xff1a;一种新颖的6自由度外参标定流程。根据三个操作规则&#xff0c;使一个多相机系统单独捕捉一些…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023