备战蓝桥杯Day21 - 堆排序的内置模块+topk问题

news2024/11/15 18:37:48

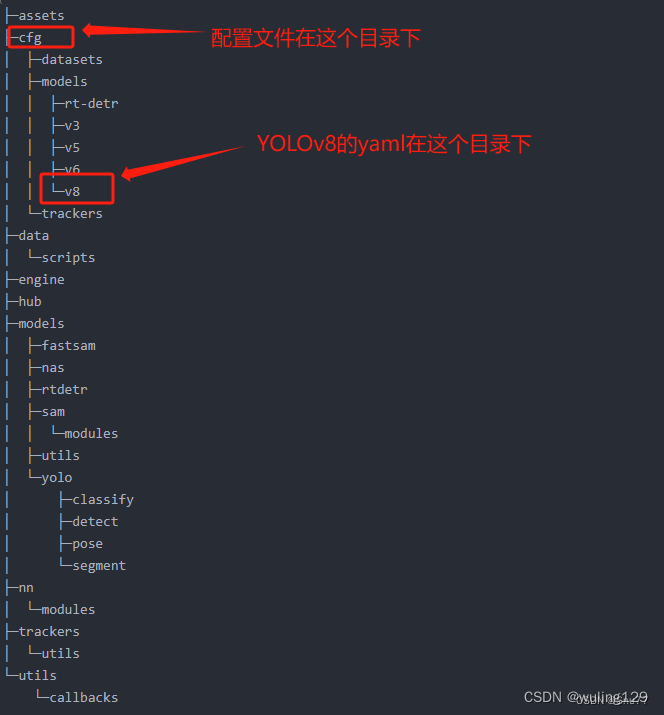
一、内置模块

在python中，堆排序已经设置好了内置模块，不想自己写的话可以使用内置模块，真的很方便，但是堆排序算法的底层逻辑最好还是要了解并掌握一下的。

使用heapq模块的heapify()函数将列表转换为堆，然后使用heappop()和heappush()函数执行堆排序操作。

代码实现

import heapq  # 导入包
import random   # 随机数库，生成随机数


li = list(range(100))
random.shuffle(li)

print(li)
heapq.heapify(li)   # 建堆的过程

# 使用内置模块实现堆排序
n = len(li)
for i in range(n):
    print(heapq.heappop(li), end=",")

二、topk问题

问题描述：现在有n个数，设计算法得到前k个大的数。（k<n）

解决思路：

取列表前k个元素建立一个小根堆。堆顶就是目前第k大的数。

依次向后遍历原列表，对于列表中的元素，如果小于堆顶，则忽略该元素；如果大于堆顶，则将堆顶更换为该元素，并且对堆顶进行一次调整。

遍历列表所有元素后，倒序弹出堆顶。

代码实现：

def sift(li, low, high):
    """

    :param li: 用列表存放树结构
    :param low: 堆的根节点位置
    :param high: 堆的最后一个元素的位置
    :return:
    """
    i = low   # i最开始指向根节点
    j = 2 * i + 1   # j最开始指向左孩子
    tmp = li[low]   # 将栈顶保存起来
    while j <= high:  # 循环条件为只要j不越过列表的界
        if j + 1 <= high and li[j+1] < li[j]:  
            j = j+1    # 那么把指针指向数字大的右孩子
        if li[j] < tmp:
            li[i] = li[j]   # 将i位置赋值为较大的数
            i = j   # 并将i，j指针向下移动
            j = 2 * i +1
        else:  # 如果tmp更大，将tmp放到i的位置上
            li[i] = tmp   # 把tmp放到某个子树的根节点上
            break
    else:
        li[i] = tmp   # 把tmp放到叶子节点上


def topk(li, k):
    heap = li[0:k]
    # 1.建堆
    for i in range((k-2)//2, -1, -1):
        sift(heap, i, k-1)
    # 2.遍历并向下调整
    for i in range(k, len(li)-1):
        if li[i] > heap[0]:
            heap[0] = li[i]   #
            sift(heap, 0, k-1)
    # 3.出数
    for i in range(k-1,-1, -1):
        heap[0], heap[i] = heap[i], heap[0]
        sift(heap, 0, i-1)
    return heap


# 测试例子
import random
li = list(range(1000))
random.shuffle(li)
print(topk(li, 10))

运行结果