1 二叉搜索树的插入操作
给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。
示例 1:
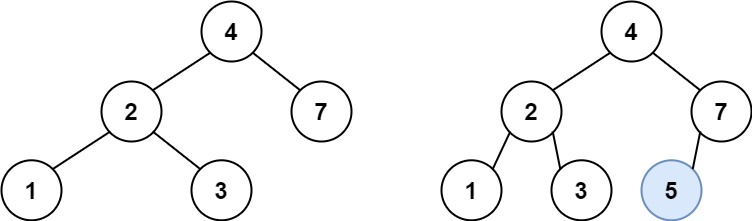
输入:root = [4,2,7,1,3], val = 5 输出:[4,2,7,1,3,5] 解释:另一个满足题目要求可以通过的树是:
示例 2:
输入:root = [40,20,60,10,30,50,70], val = 25 输出:[40,20,60,10,30,50,70,null,null,25]
示例 3:
输入:root = [4,2,7,1,3,null,null,null,null,null,null], val = 5 输出:[4,2,7,1,3,5]
法1:递归
插入的数据比当前节点数据小,向左子树递归;
插入的数据比当前节点数据大,向右子树递归。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
// 空节点
if (root == nullptr) {
return new TreeNode(val);
}
if (root->val > val) {
root->left = insertIntoBST(root->left, val);
}
if (root->val < val) {
root->right = insertIntoBST(root->right, val);
}
return root;
}
};法2:迭代
记录遍历的前一个节点,遍历到叶子节点,此时:
如果前一个节点大于当前节点,则将插入数据放到前一个节点的左子树上;
如果前一个节点小于当前节点,则将插入数据放到前一个节点的右子树上;再分别递归左右子树
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* preNode = nullptr;
void helper(TreeNode* root, int val) {
// 遍历到叶子节点上
if (root == nullptr) {
TreeNode* node = new TreeNode(val);
// 插到左子树上
if (preNode->val > val) {
preNode->left = node;
} else if (preNode->val < val) {
preNode->right = node;
}
return;
}
// 更新前一个节点
preNode = root;
// 左右递归
if (root->val > val) {
helper(root->left, val);
}
if (root->val < val) {
helper(root->right, val);
}
}
TreeNode* insertIntoBST(TreeNode* root, int val) {
if (root == nullptr) {
return new TreeNode(val);
}
helper(root, val);
return root;
}
};2 二叉搜索树的删除操作
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
- 首先找到需要删除的节点;
- 如果找到了,删除它。
示例 1:
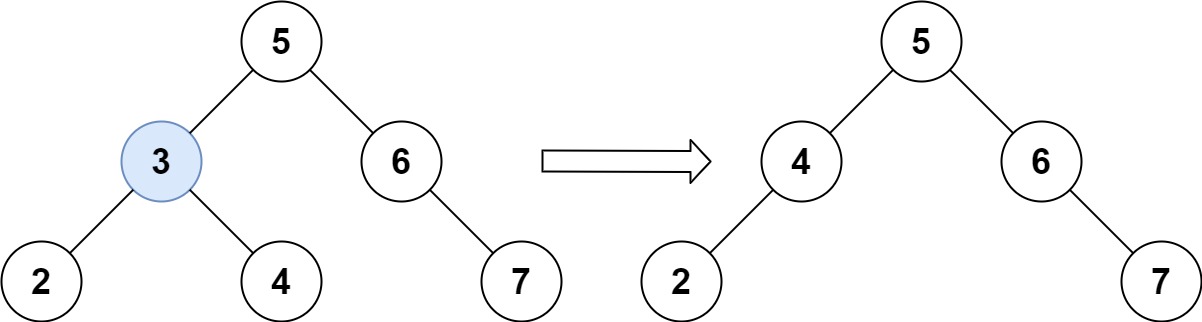
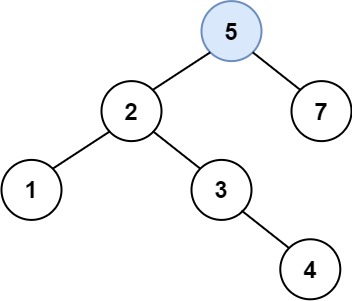
输入:root = [5,3,6,2,4,null,7], key = 3 输出:[5,4,6,2,null,null,7] 解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。 一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。 另一个正确答案是 [5,2,6,null,4,null,7]。
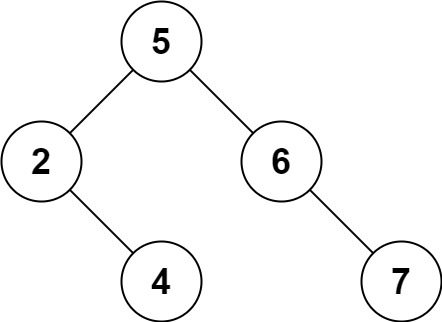
示例 2:
输入: root = [5,3,6,2,4,null,7], key = 0 输出: [5,3,6,2,4,null,7] 解释: 二叉树不包含值为 0 的节点
示例 3:
输入: root = [], key = 0 输出: []
情况1:该节点为空,直接返回nullptr;
情况2:要删除的是叶子节点,即没有左右子树,直接删除即可;
情况3:要删除的节点有左子树,删除该节点,左子树补位;
情况4:要删除的节点有右子树,删除该节点,右子树补位;
情况5:要删除的节点左右子树都有,将该节点的左子树查到该节点右子树的最左子树,删除该节点。
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if (root == nullptr) {
return nullptr;
}
if (root->val == key) {
if (root->left == nullptr && root->right == nullptr) {
delete root;
return nullptr;
} else if (root->left != nullptr && root->right == nullptr) {
TreeNode* node = root;
root = root->left;
delete node;
return root;
} else if (root->left == nullptr && root->right != nullptr) {
TreeNode* node = root;
root = root->right;
delete node;
return root;
} else if (root->left != nullptr && root->right != nullptr) {
// 情况5:要删除的节点左右子树都有,将该节点的左子树查到该节点右子树的最左子树,删除该节点。
TreeNode* curNode = root->right;
while (curNode->left != nullptr) {
curNode = curNode->left;
}
curNode->left = root->left;
TreeNode* node = root;
root = root->right;
delete node;
return root;
}
}
if (root->val > key) {
root->left = deleteNode(root->left, key);
}
if (root->val < key) {
root->right = deleteNode(root->right, key);
}
return root;
}
};3 二叉搜索树的转换操作
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
示例 1:
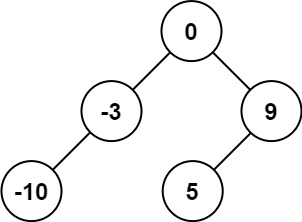
输入:nums = [-10,-3,0,5,9] 输出:[0,-3,9,-10,null,5] 解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:

示例 2:
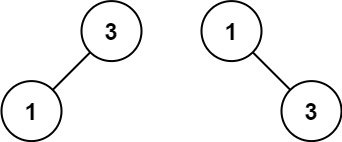
输入:nums = [1,3] 输出:[3,1] 解释:[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。
直接递归
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* helper(vector<int>& nums, int i, int j) {
if (i > j) {
return nullptr;
}
int mid = i + (j - i) / 2;
TreeNode* root = new TreeNode(nums[mid]);
root->left = helper(nums, i, mid - 1);
root->right = helper(nums, mid + 1, j);
return root;
}
TreeNode* sortedArrayToBST(vector<int>& nums) {
return helper(nums, 0, nums.size() - 1);
}
};链接:
[1] 701. 二叉搜索树中的插入操作 - 力扣(LeetCode)
[2] . - 力扣(LeetCode)
[3] . - 力扣(LeetCode)