前言:
VAE——Variational Auto-Encoder,变分自编码器,是由 Kingma 等人于 2014 年提出的基于变分贝叶斯(Variational Bayes,VB)推断的生成式网络结构。与传统的自编码器通过数值的方式描述潜在空间不同,它以概率的方式描述对潜在空间的观察,在数据生成方面表现出了巨大的应用价值。VAE一经提出就迅速获得了深度生成模型领域广泛的关注,并和生成对抗网络(Generative Adversarial Networks,GAN)被视为无监督式学习领域最具研究价值的方法之一,在深度生成模型领域得到越来越多的应用。
Durk Kingma 目前也是 OpenAI 的研究科学家
VAE 是我深度学习过程中偏难的一部分,涉及到的理论基础:
极大似然估计, KL 散度 ,Bayes定理,蒙特卡洛重采样思想,VI变分思想,ELBO
目录:
- AE 编码器缺陷
- VAE 编码器 跟AE 编码器差异
- VAE 编码器
- VAE 思想
- Python 代码例子
一 AE 编码器缺陷
1.1 AE 简介
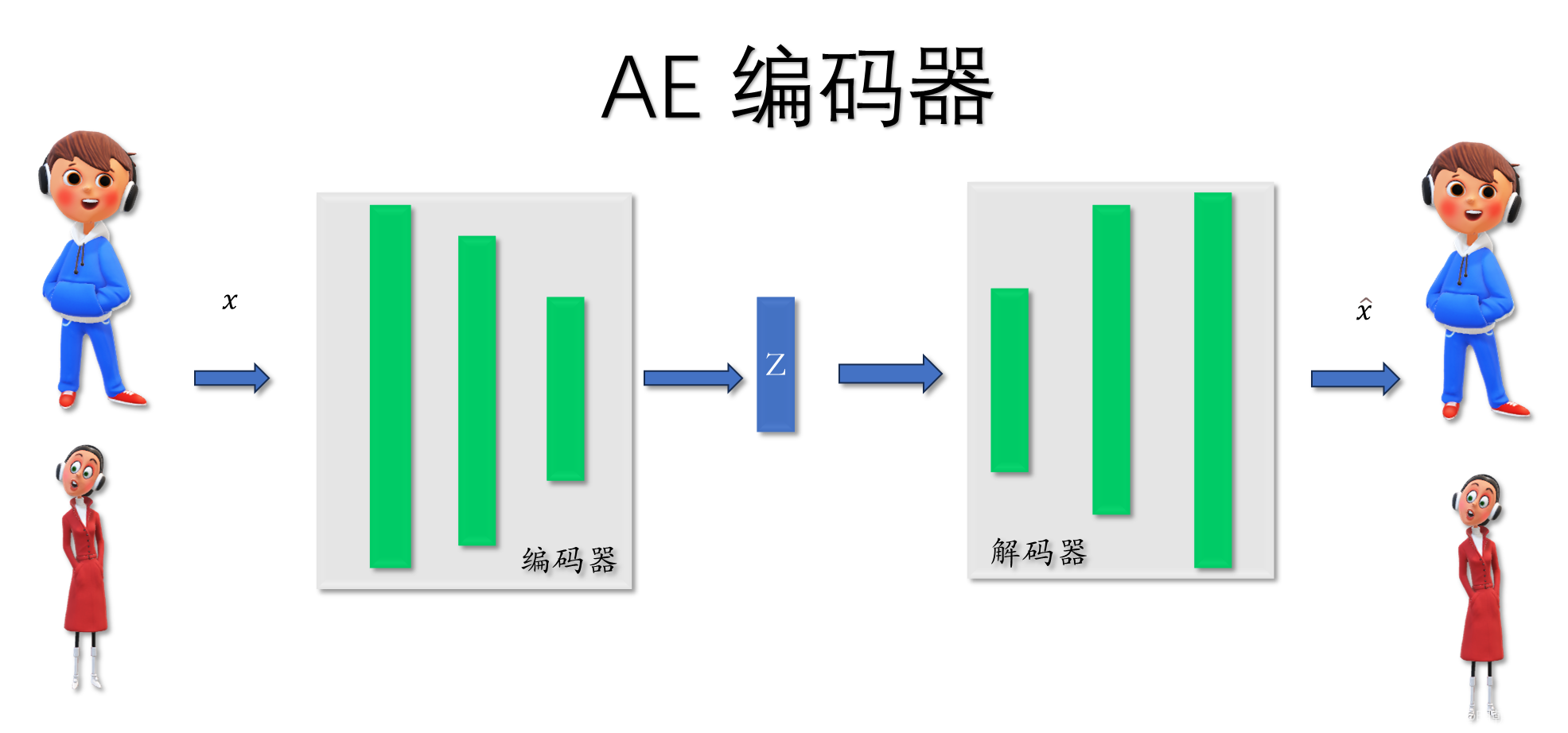
输入一张图片
编码器Encoder:
通过神经网络得到低维度的特征空间Z
解码器Decoder:
通过特征空间 重构输入的图像
损失函数:
1.2 特征空间z
单独使用解码器Decoder
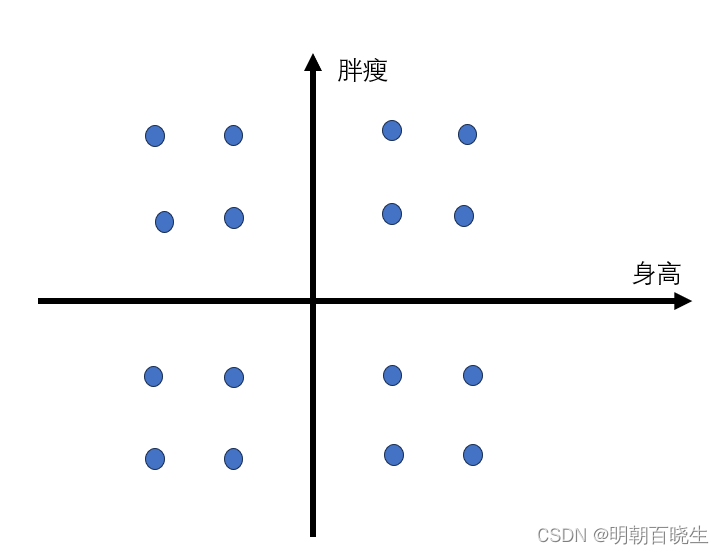
特征空间z 维度为10,固定其它维度参数. 取其中两维参数,产生不同的
值(如下图星座图),然后通过Decoder 生成不同的图片.就会发现该维度
跟图像的某些特征有关联.
1.3 通过特征空间z重构缺陷:泛化能力差
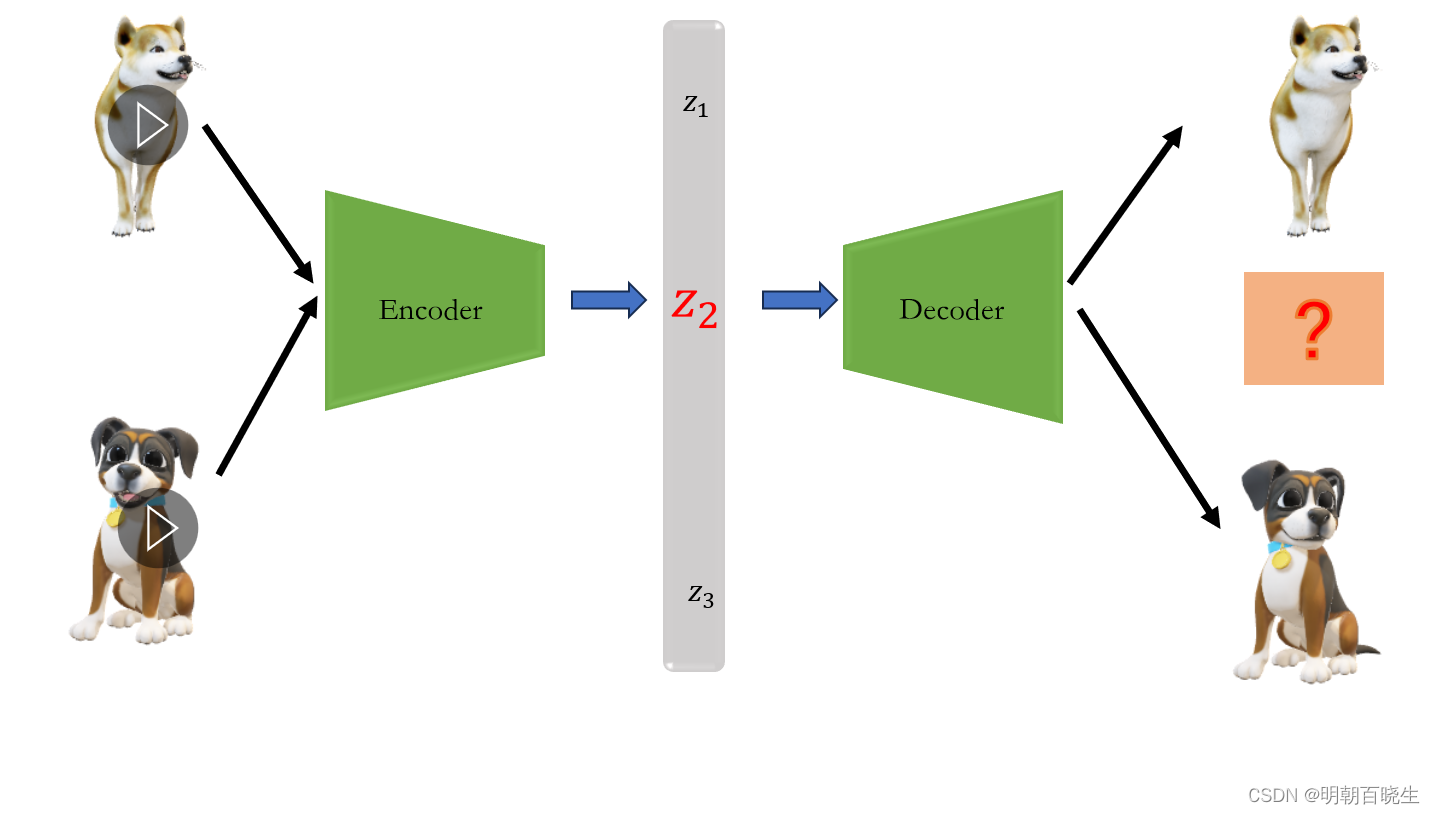
如上图:
假设通过AE 模型训练动物的图像,特征空间Z为一维度。
两种狗分别对应特征向量, 我们取一个特征向量
,期望通过
解码器输出介于两种狗中间的一个样子的一种狗。
实际输出: ,随机输出一些乱七八糟的图像。
原因:
因为训练的时候,模型对训练的图像和特征空间Z的映射是离散的,对特征空间z
中没有训练过的空间没有约束,所以通过解码器输出的图像也是随机的.
二 VAE 编码器 跟AE 编码器差异
2.1 AE 编码器特征空间
假设特征空间Z 为一维,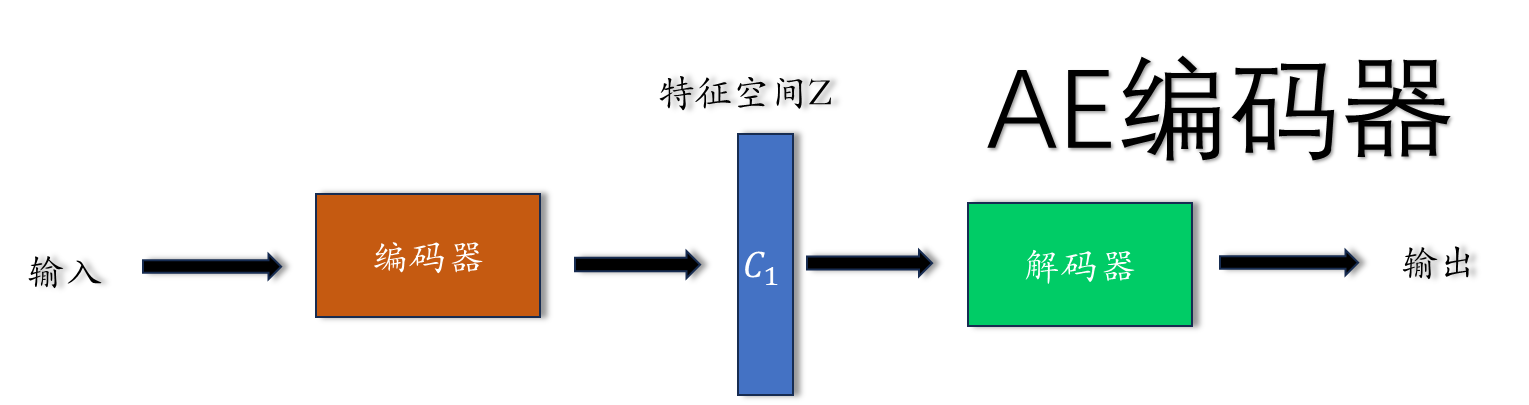
通过编码器生成的特征空间为一维空间的一个离散点c,然后通过解码器重构输入x
2.2 VAE 编码器
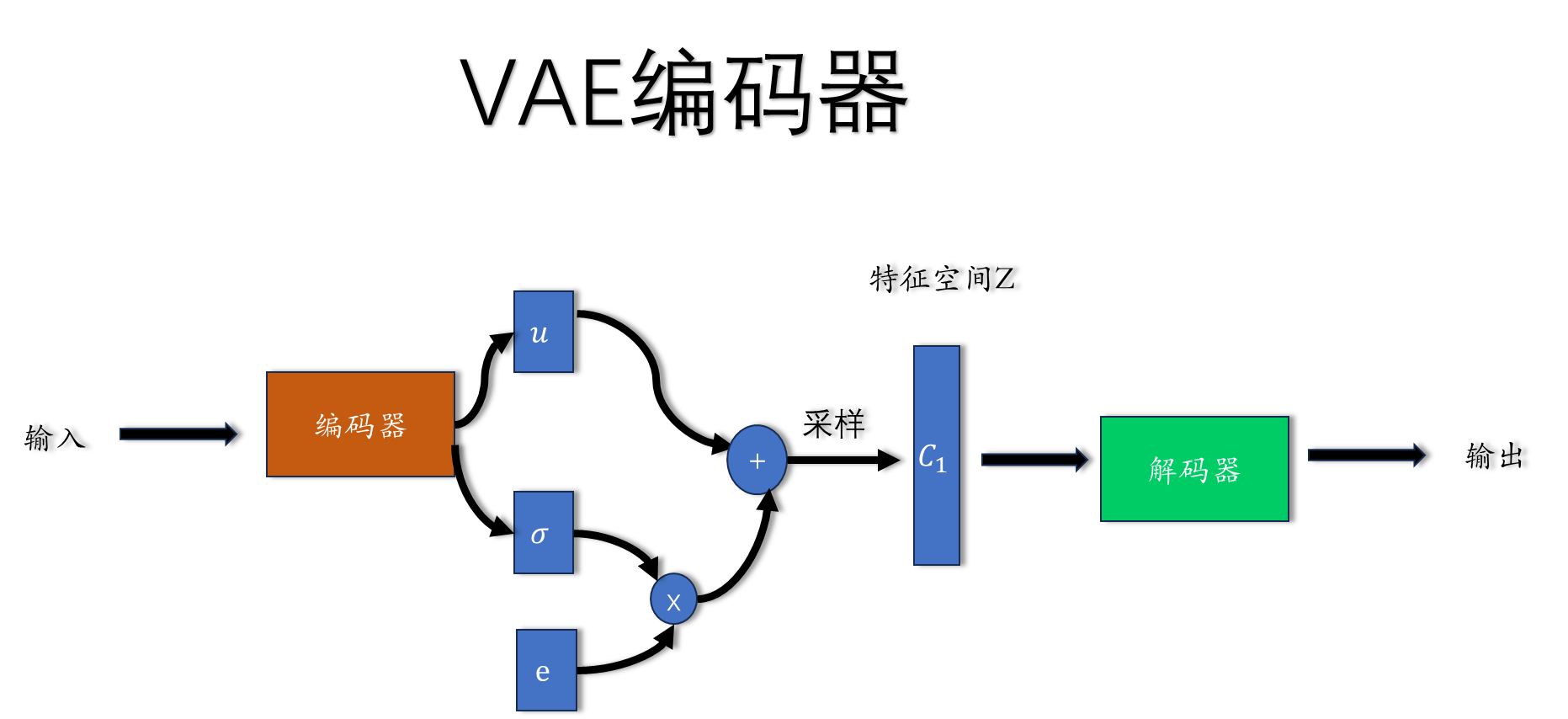

通过编码器产生一个均值为u,方差为的高斯分布,然后在该分布上采样得到
特征空间的一个点, 通过解码器重构输入. 现在特征空间Z是一个高斯分布,
泛化能力更强
三 VAE 编码器
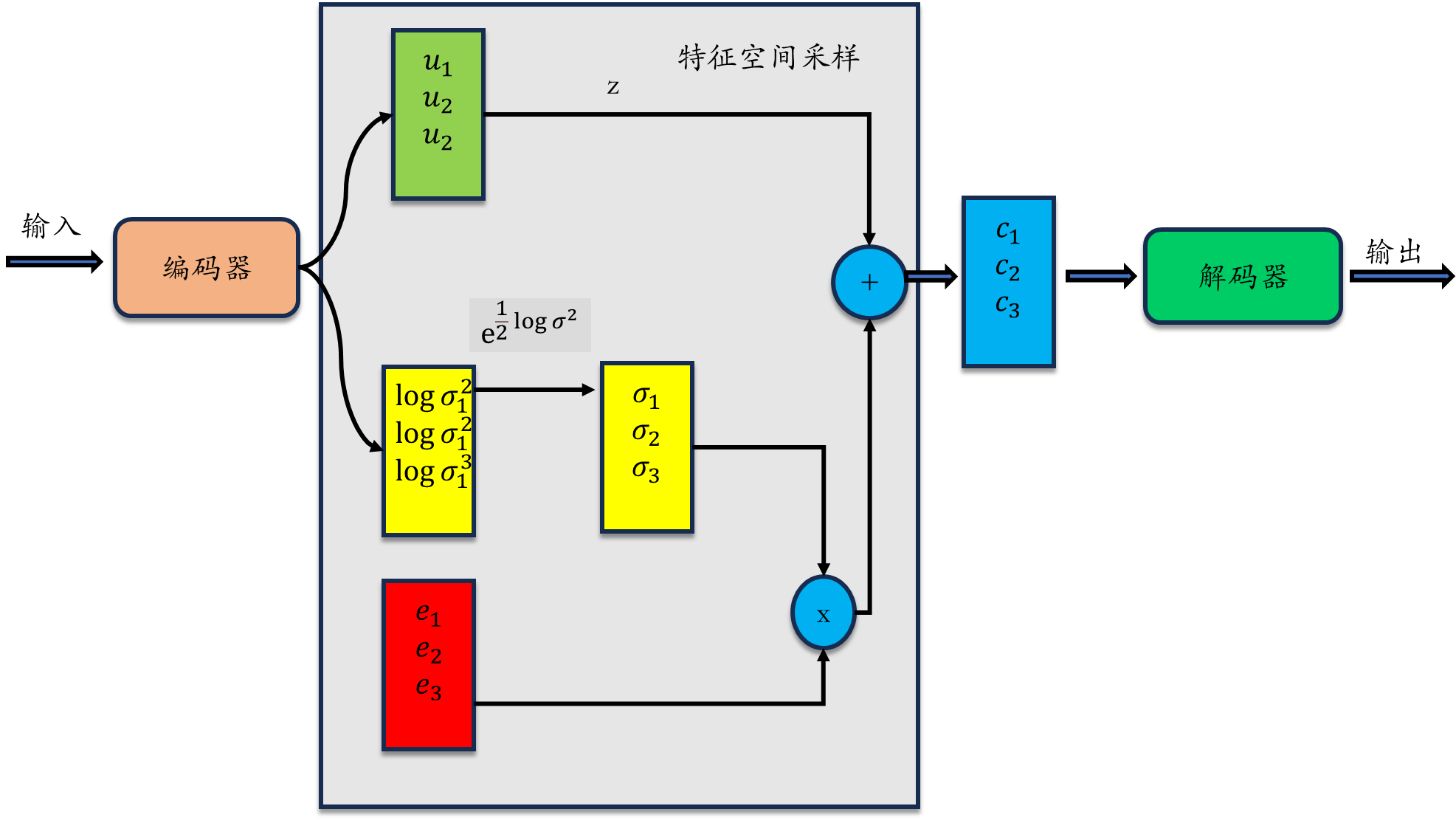
3.1 模型简介
输入 :
经过编码器 生成一个服从高斯分布的特征空间 ,
通过重参数采样技巧 采样出特征点
把特征点 输入解码器,重构出输入x
3.2 标准差(黄色模块)设计原理
方差 标准差
因为标准差是非负的,但是经过编码器输出的可能是负的值,所以
认为其输出值为 ,再经过 exp 操作,得到一个非负的标准差
很多博主用的,我理解是错误的,为什么直接用 标准差
参考3.3 苏剑林的 重参数采样 原理画出来的。

3.3 为什么要重参数采样 reparameterization trick
我们要从中采样一个Z出来,尽管我们知道了
是正态分布,但是均值方差都是靠模型算出来的,我们要靠这个过程反过来优化均值方差的模型。
但是“采样”这个操作是不可导的,而采样的结果是可导的。
的概率可以写成如下形式
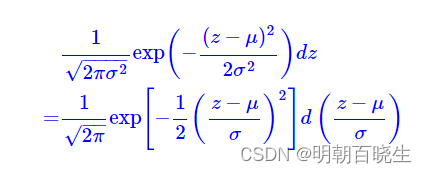
说明
 服从 N(0,1)的标准正态分布
服从 N(0,1)的标准正态分布
从中采样一个Z,相当于从N(0,I)标准正态分布中采样一个e,然后让
我们将从采样变成了从N(0,I)中采样,然后通过参数变换得服从
分布。这样一来,“采样”这个操作就不用参与梯度下降了,改为采样的结果参与,使得整个模型可训练了。其中
是求导参数,e 为已知道参数
3.4 损失函数
该模型有两个约束条件
1 一个输入图像和重构的图像
,mse 误差最小
2 特征空间Z 要服从高斯分布(使用KL 散度)
该值越小越好
KL 散度简化

3.5 伪代码

四 VAE 思想
4.1 高斯混合模型
我们重构出m张图片
,
很复杂无法求解.
常用的思路是通过引入隐藏变量(latent variable) Z。
寻找 Z空间到 X空间的映射,这样我们通过在Z空间采样映射到 X 空间就可以生成新的图片。
我们使用多个高斯分布的 去拟合
的分布,这里面
为已知道
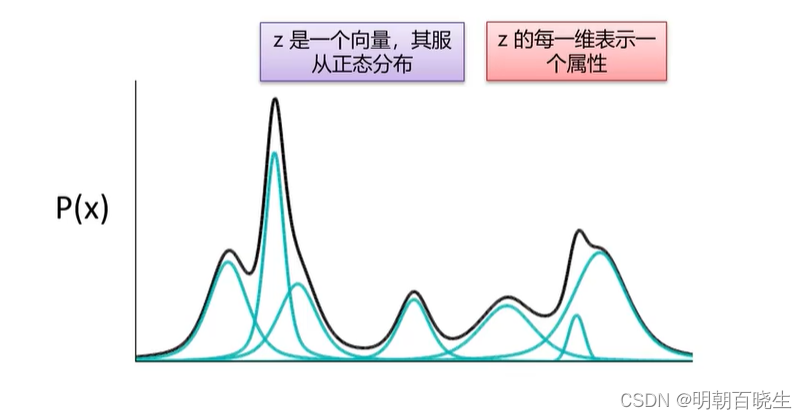
在强化学习里面,蒙特卡罗重采样也是用了该方案.
例:

如上图 P(X=红色)=2/5 ,P(X=绿色)=3/5
我们可以通过高斯混合模型原理的方法求解
P(X=红色)=P(X=红色|Z=正方形)*P(Z=正方形)+ P(X=红色|Z=圆形)*P(Z=圆形)
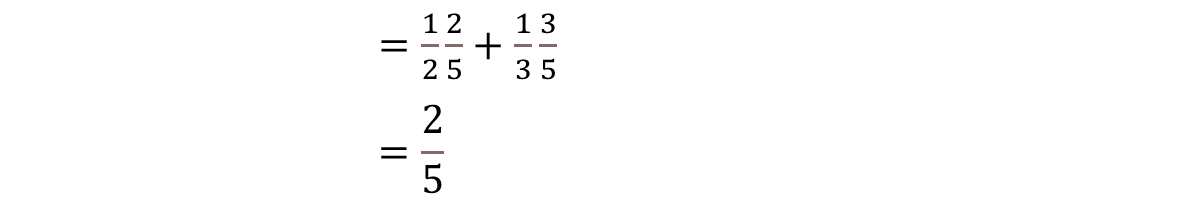
P(X=绿色)也是一样
4.2 极大似然估计

目标:极大似然函数
已知:
编码器的概率分布
则:
(相当于乘以1)
(因为P(x)跟z 无关,可以直接拿到积分里面)
贝叶斯定理:
1: VAE叫做“变分自编码器”,它跟变分法有什么联系
固定概率分布p(x)(或q(x)的情况下,对于任意的概率分布q(x)(或p(x))),都有KL(p(x)||q(x))≥0,而且只有当p(x)=q(x)时才等于零。
因为KL(p(x)∥∥q(x))实际上是一个泛函,要对泛函求极值就要用到变分法
ELBO:全称为 Evidence Lower Bound,即证据下界。
上面KL(q(z|x)||q(z|x)) 我们取了下界0
贝叶斯定理
注意: 这里面P(Z)在4.1 高斯混合模型 是已知道的概率分布,符合高斯分布
我们目标值是求L 的最大值
第一项:
因为KL 散度的非负性
极大值点为
,因为p(z)是符合高斯分布的
所以通过编码器生成的q(z|x)也要跟它概率一致,符合高斯分布。
第二项:

这部分代表重构误差,我们用
来训练该部分的误差
五 Python 代码
# -*- coding: utf-8 -*-
"""
Created on Mon Feb 26 15:47:20 2024
@author: chengxf2
"""
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms # transforms用于数据预处理
# 定义变分自编码器(VAE)模型
class VAE(nn.Module):
def __init__(self, latent_dim):
super(VAE, self).__init__()
# Encoder
self.encoder = nn.Sequential(
nn.Linear(in_features=784, out_features=256),
nn.ReLU(),
nn.Linear(in_features=256, out_features=128),
nn.ReLU(),
nn.Linear(in_features=128, out_features=latent_dim*2), # 输出均值和方差
nn.ReLU()
)
# Decoder
self.decoder = nn.Sequential(
nn.Linear(in_features =latent_dim , out_features=128),
nn.ReLU(),
nn.Linear(in_features=128, out_features=256),
nn.ReLU(),
nn.Linear(in_features=256, out_features=784),
nn.Sigmoid()
)
def reparameterize(self, mu, logvar):
std = torch.exp(logvar/2.0) # 计算标准差,Encoder 出来的可能有负的值,标准差为非负值,所以要乘以exp
eps = torch.randn_like(std) # 从标准正态分布中采样噪声
z = mu + eps * std # 重参数化技巧
return z
def forward(self, x):
# 编码[batch, latent_dim*2]
encoded = self.encoder(x)
#[ z = mu|logvar]
mu, logvar = torch.chunk(encoded, 2, dim=1) # 将输出分割为均值和方差
z = self.reparameterize(mu, logvar) # 重参数化
# 解码
decoded = self.decoder(z)
return decoded, mu, logvar
# 定义训练函数
def train_vae(model, train_loader, num_epochs, learning_rate):
criterion = nn.BCELoss() # 二元交叉熵损失函数
optimizer = optim.Adam(model.parameters(), lr=learning_rate) # Adam优化器
model.train() # 设置模型为训练模式
for epoch in range(num_epochs):
total_loss = 0.0
for data in train_loader:
images, _ = data
images = images.view(images.size(0), -1) # 展平输入图像
optimizer.zero_grad()
# 前向传播
outputs, mu, logvar = model(images)
# 计算重构损失和KL散度
reconstruction_loss = criterion(outputs, images)
kl_divergence = 0.5 * torch.sum( -logvar +mu.pow(2) +logvar.exp()-1)
# 计算总损失
loss = reconstruction_loss + kl_divergence
# 反向传播和优化
loss.backward()
optimizer.step()
total_loss += loss.item()
# 输出当前训练轮次的损失
print('Epoch [{}/{}], Loss: {:.4f}'.format(epoch+1, num_epochs, total_loss / len(train_loader)))
print('Training finished.')
# 示例用法
if __name__ == '__main__':
# 设置超参数
latent_dim = 32 # 潜在空间维度
num_epochs = 1 # 训练轮次
learning_rate = 1e-4 # 学习率
# 加载MNIST数据集
train_dataset = torchvision.datasets.MNIST(root='./data', train=True, transform=transforms.ToTensor(), download=True)
train_loader = torch.utils.data.DataLoader(dataset=train_dataset, batch_size=100, shuffle=True)
# 创建VAE模型
model = VAE(latent_dim)
# 训练VAE模型
train_vae(model, train_loader, num_epochs, learning_rate)
,
VAE到底在做什么?VAE原理讲解系列#1_哔哩哔哩_bilibili
VAE里面的概率知识。VAE原理讲解系列#2_哔哩哔哩_bilibili
vae损失函数怎么理解? - 知乎
如何搭建VQ-VAE模型(Pytorch代码)_哔哩哔哩_bilibili
变分自编码器(一):原来是这么一回事 - 科 学空间|Scientific Spaces
16: Unsupervised Learning - Auto-encoder_哔哩哔哩_bilibili
【生成模型VAE】十分钟带你了解变分自编码器及搭建VQ-VAE模型(Pytorch代码)!简单易懂!—GAN/机器学习/监督学习_哔哩哔哩_bilibili
[diffusion] 生成模型基础 VAE 原理及实现_哔哩哔哩_bilibili
[论文简析]VAE: Auto-encoding Variational Bayes[1312.6114]_哔哩哔哩_bilibili