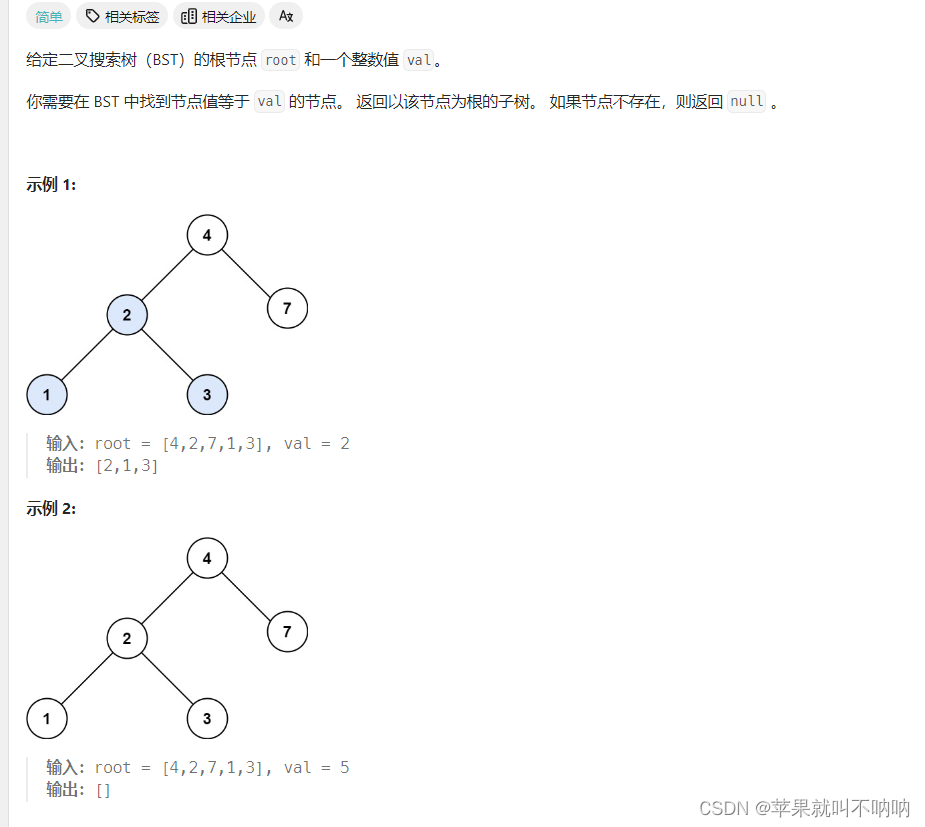
【二叉搜索树】【递归】【迭代】Leetcode 700. 二叉搜索树中的搜索
- 二叉搜索树
- 解法1 递归法
- 解法2 迭代法
---------------🎈🎈题目链接🎈🎈-------------------
二叉搜索树
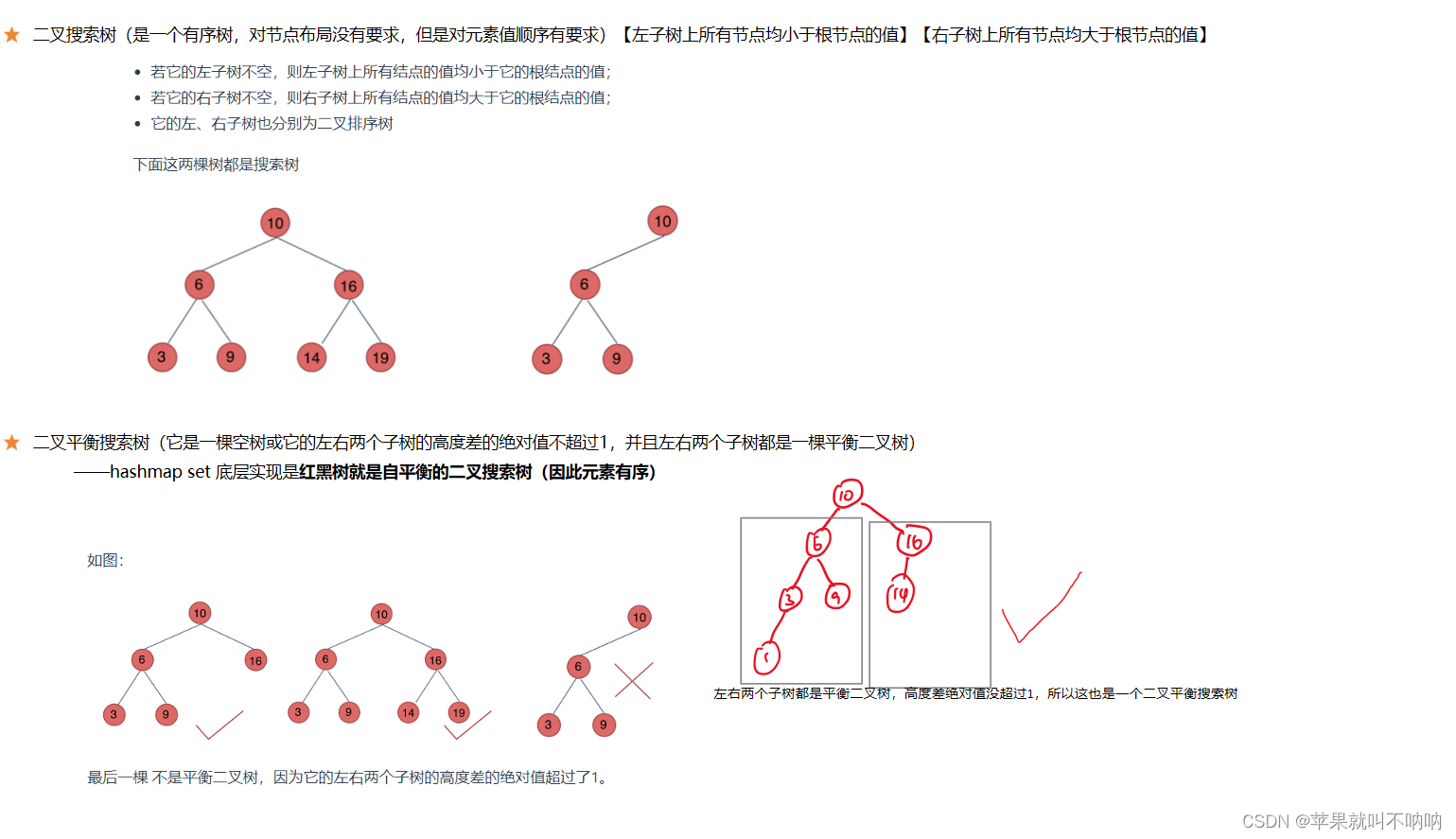
二叉搜索树(Binary Search Tree,BST)是一种特殊的二叉树,具有以下性质:
有序性: 对于二叉搜索树中的每个节点,其左子树中的所有节点的值都小于该节点的值,而右子树中的所有节点的值都大于该节点的值。这意味着对于任何节点,其左子树中的值都小于该节点的值,右子树中的值都大于该节点的值。
唯一性: 二叉搜索树中不存在重复的节点。
搜索操作: 由于二叉搜索树的有序性,可以利用二分查找的思想进行快速的搜索。给定一个值,可以从根节点开始比较,根据比较结果决定是向左子树还是向右子树搜索,直到找到目标节点或者搜索到叶子节点为止。
插入操作: 插入操作也是根据节点值的大小关系进行的。从根节点开始,比较要插入的节点值与当前节点值的大小关系,如果小于当前节点值,则继续在左子树中插入;如果大于当前节点值,则继续在右子树中插入。直到找到合适的位置插入新节点。
删除操作: 删除操作相对复杂一些。如果要删除的节点是叶子节点,则可以直接删除;如果要删除的节点只有一个子节点,则将其子节点替换到被删除节点的位置;如果要删除的节点有两个子节点,则通常选择该节点的前驱节点或者后继节点来替换被删除节点,并递归地删除用于替换的节点。
二叉搜索树的这些性质使得其在搜索、插入和删除等操作上具有较高的效率。然而,如果树的结构不平衡(比如极端情况下,树退化成链表),则操作的时间复杂度可能会退化到O(n),而不再是平衡状态下的O(log n)。因此,在实际应用中,通常会考虑使用平衡二叉搜索树(如AVL树、红黑树等)来保持搜索性能的稳定。
解法1 递归法
时间复杂度:在最坏情况下,时间复杂度为 O(h),其中 h 是树的高度。在一个平衡的二叉搜索树中,树的高度近似为 log(n),其中 n 是树中节点的数量。但是在最坏情况下,树可能会退化成链表,高度为 n。因此,在最坏情况下,时间复杂度为 O(n),在平均情况下,为 O(log n)。
空间复杂度:递归调用的栈空间取决于树的高度,因此空间复杂度也是 O(h)。在最坏情况下,树可能会退化成链表,空间复杂度为 O(n),在平均情况下,为 O(log n)。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode searchBST(TreeNode root, int val) {
return helper(root,val);
}
public TreeNode helper(TreeNode root, int val){
if(root == null) return null;
if(root.val == val) return root;
else if(root.val>val) {
return searchBST(root.left,val);
}
else {
return searchBST(root.right,val);
}
}
}
解法2 迭代法
时间复杂度:在最坏情况下,时间复杂度为 O(h),其中 h 是树的高度。在一个平衡的二叉搜索树中,树的高度近似为 log(n),其中 n 是树中节点的数量。但是在最坏情况下,树可能会退化成链表,高度为 n。因此,在最坏情况下,时间复杂度为 O(n),在平均情况下,为 O(log n)。
空间复杂度:这种迭代方法不使用递归,只使用了常量级的额外空间,因此空间复杂度是 O(1)。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode searchBST(TreeNode root, int val) {
// 迭代法
while(root != null){
if(root.val > val){
root = root.left;
}
else if(root.val < val){
root = root.right;
}
else{
return root;
}
}
return null;
}
}