一个写得很好的博客：
图或网络中的中心性：点度中心性、中介中心性、接近中心性、特征向量中心性、PageRank

特征向量中心性（eigenvector centrality）
特征向量中心性的基本思想是，一个节点的中心性是相邻节点中心性的函数。也就是说，与你连接的人越重要，你也就越重要。

特征向量中心性和点度中心性不同，一个点度中心性高即拥有很多连接的节点特征向量中心性不一定高，因为所有的连接者有可能特征向量中心性很低。同理，特征向量中心性高并不意味着它的点度中心性高，它拥有很少但很重要的连接者也可以拥有高特征向量中心性。

以上这些指标也可以直接掉包计算得到。关于networks包的使用详见博客https://www.cnblogs.com/ljhdo/p/10662902.html

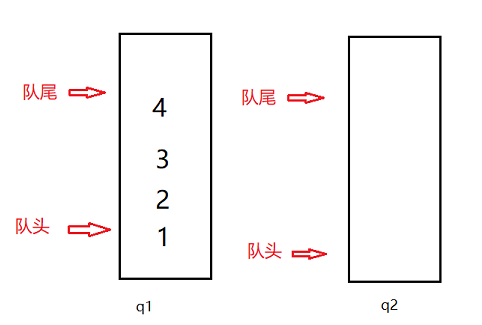
举个例子定义一个这样的无向图(忽略箭头，假装这是一个无向图，因为用csdn的mermaid只能画有向图)

代码如下：

import numpy as np
import pandas as pd
import networkx as nx

#利用pandas库的DataFrame()函数构建一个类似于字典的东西
edges = pd.DataFrame()
edges['sources'] = [1,1,1,2,2,3,3,4,4,5,5,5]
edges['targets'] = [2,4,5,3,1,2,5,1,5,1,3,4]
edges['weights'] = [1,1,1,1,1,1,1,1,1,1,1,1]

# 给图G添加有权边，sources是起始点，targets是终点，
# 两点确定一条直线，即节点之间的边，
# 第三个参数是边权
G = nx.from_pandas_edgelist(edges,source='sources',target='targets',edge_attr='weights')

#degree,返回5个节点的度视图
print('度:',nx.degree(G))
# [(1, 3), (2, 2), (4, 2), (5, 3), (3, 2)]
# 这个结果指的是1节点度为3, 2节点度为2...,以此类推

#连通分量
print('连通分量:',list(nx.connected_components(G)))
#图直径
print('图直径:',nx.diameter(G))
#度中心性
print('度中心性:',nx.degree_centrality(G))
#特征向量中心性
print('特征向量中心性:',nx.eigenvector_centrality(G))
#betweenness
print('中介中心性:',nx.betweenness_centrality(G))
#closeness
print('接近中心性:',nx.closeness_centrality((G)))
print('pagerank:',nx.pagerank((G)))
print('hits:',nx.hits((G)))

# 连通分量: [{1, 2, 3, 4, 5}]
# 图直径: 2
# 度中心性: {1: 0.75, 2: 0.5, 4: 0.5, 5: 0.75, 3: 0.5}
# 特征向量中心性: {1: 0.5298988890761731, 2: 0.35775191431708964, 4: 0.4271316779596084, 5: 0.5298988890761731, 3: 0.35775191431708964}
# 中介中心性: {1: 0.25, 2: 0.08333333333333333, 4: 0.0, 5: 0.25, 3: 0.08333333333333333}
# 接近中心性: {1: 0.8, 2: 0.6666666666666666, 4: 0.6666666666666666, 5: 0.8, 3: 0.6666666666666666}
# pagerank: {1: 0.24369622576677996, 2: 0.17225629712058638, 4: 0.16809495422526693, 5: 0.2436962257667799, 3: 0.17225629712058638}
# hits: ({1: 0.24059715195481507, 2: 0.1624345647450478, 4: 0.19393656660027417, 5: 0.2405971519548151, 3: 0.1624345647450478}, {1: 0.2405971522393837, 2: 0.1624345646565165, 4: 0.19393656620819955, 5: 0.2405971522393837, 3: 0.1624345646565165})