丢失的MD5

题目：（就一python文件，MD5.py）

for i in range(32,127):
    for j in range(32,127):
        for k in range(32,127):
            m=hashlib.md5()
            m.update('TASC'+chr(i)+'O3RJMV'+chr(j)+'WDJKX'+chr(k)+'ZM')
            des=m.hexdigest()
            if 'e9032' in des and 'da' in des and '911513' in des:
                print des 

代码有点问题，跑不起来，改一下：

import hashlib
for i in range(32, 127):
    for j in range(32, 127):
        for k in range(32, 127):
            m = hashlib.md5()
            data = 'TASC' + chr(i) + 'O3RJMV' + chr(j) + 'WDJKX' + chr(k) + 'ZM'
            m.update(data.encode('utf-8'))
            des = m.hexdigest()
            if 'e9032' in des and 'da' in des and '911513' in des:
                print(data, des)

我感觉这题最难的是猜他要干什么，我开始哪想到flag就是des结果啊
flag{e9032994dabac08080091151380478a2}

Quoted-printable

http://www.hiencode.com/quoted.html
题目就把答案写上了

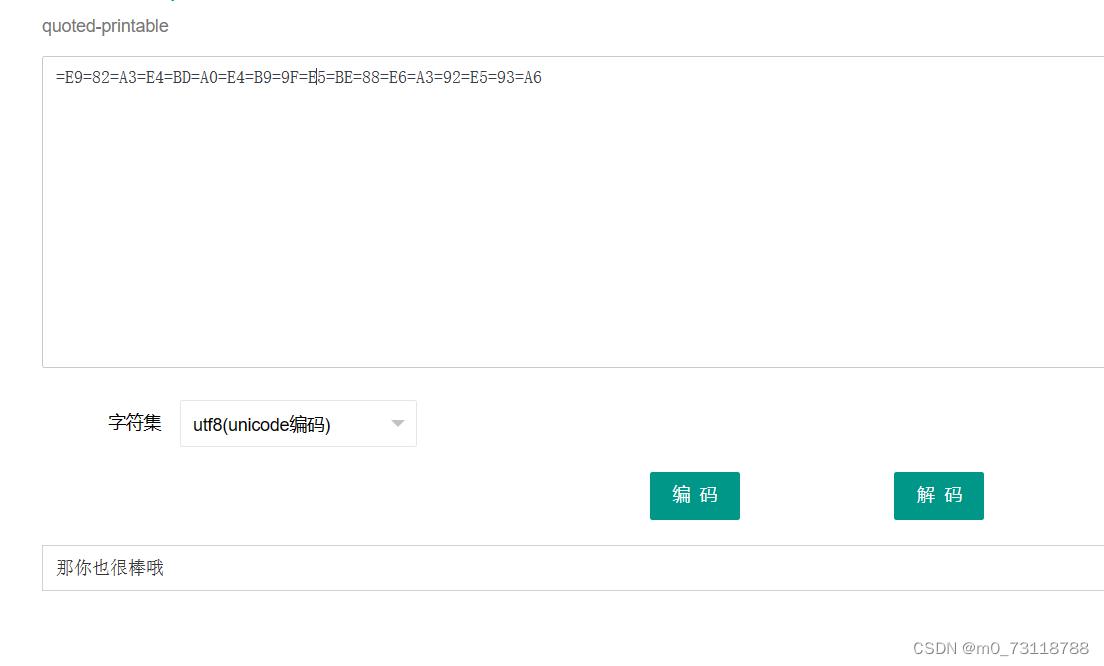
flag{那你也很棒哦}

RSA

题目：在一次RSA密钥对生成中，假设p=473398607161，q=4511491，e=17
求解出d作为flga提交
代码用了扩展欧几里得算法

def egcd(a, b):
    if a == 0:
        return (b, 0, 1)
    else:
        g, y, x = egcd(b % a, a)
        return (g, x - (b // a) * y, y)

def modinv(a, m):
    g, x, y = egcd(a, m)
    if g != 1:
        raise Exception('Modular inverse does not exist')
    else:
        return x % m
p = 473398607161
q = 4511491
e = 17
n = p * q
phi = (p - 1) * (q - 1)
d = modinv(e, phi)
print("计算得到的私钥 d 为:", d)

flag{125631357777427553}