目录
- 极值理论介绍
- GEV
- POT
- 代码实现
极值理论介绍
在风险管理中,将事件分为高频高损、高频低损、低频高损、低频低损。其中低频高损是一种非常棘手的损失事件,常出现在市场大跌、金融体系崩溃、金融危机以及自然灾害等事件中。
由于很难给极端事件一个准确的定义,所以可观测的历史数据非常少。这种问题不仅仅出现在风险管理领域,在其他行业也很普遍。
极值理论(Extreme-value theory )是统计学的一种专门用于研究随机变量分布的极端尾部行为。与一般的中心趋势型统计方法不同,中心趋势性统计方法核心是中心极限定理,但是极端值无法应用中心极限定理(中心极限定理假设样本数量足够大时服从正态分布)。
GEV
假设一个随机损失变量X是独立同分布的(iid)。从F(x)中抽取的一个样本大小为n,且该样本的最大值为M(如果n很大,我们可以把M看作一个极值)。根据Fisher-Tippett定理,当n变大时,极值(即Mn)的分布收敛到下面的广义极值(GEV)分布
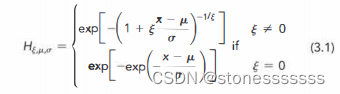
其中
μ
\mu
μ:极端值的平均数
σ \sigma σ:极端值的标准差
ϵ \epsilon ϵ:形状参数,描述极值分布的尾部形状
当
ϵ
>
0
\epsilon>0
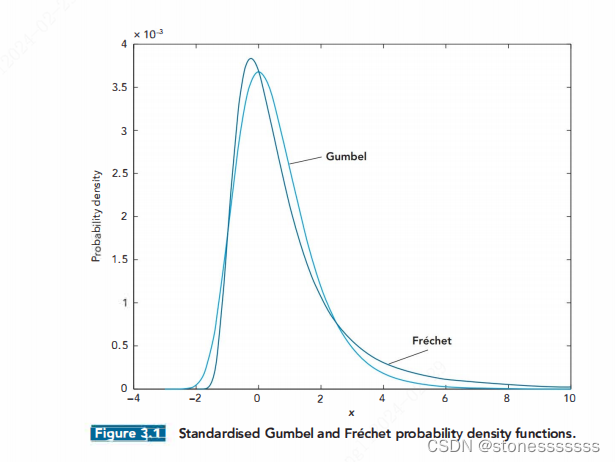
ϵ>0,服从Frechet分布,呈现出肥尾的特点。比如t分布,帕累托分布。
当
ϵ
=
0
\epsilon=0
ϵ=0,服从Gumbel分布,呈现出指数型尾部,尾部相对瘦(light)。比如正态分布,对数正态分布。
当
ϵ
<
0
\epsilon<0
ϵ<0,服从Weibull分布,呈现出比正态分布尾部更瘦的形态。该分布尤其不适用在金融实证中,由于金融数据一般呈现肥尾的特点。
POT
GEV在实际应用中可能会漏掉极值点,POT在此基础上进行改良,先设定一个阈值(threshold),超过阈值的损失分布服从POT分布,这种方法比GEV方法需要更少的参数。
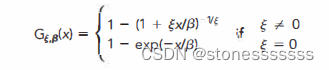
β
\beta
β:规模参数
ϵ \epsilon ϵ:形状参数,描述极值分布的尾部形状
由此可推导VaR和ES的计算方法:
V
a
R
=
μ
+
β
ϵ
{
[
n
N
u
(
1
−
α
)
−
ϵ
]
−
1
}
VaR=\mu+\frac{\beta}{\epsilon}\{[\frac{n}{N_{u}}(1-\alpha)^{-\epsilon}]-1\}
VaR=μ+ϵβ{[Nun(1−α)−ϵ]−1}
E
S
=
V
a
R
1
−
ϵ
+
β
−
ϵ
μ
1
−
ϵ
ES = \frac{VaR}{1-\epsilon}+\frac{\beta-\epsilon\mu}{1-\epsilon}
ES=1−ϵVaR+1−ϵβ−ϵμ
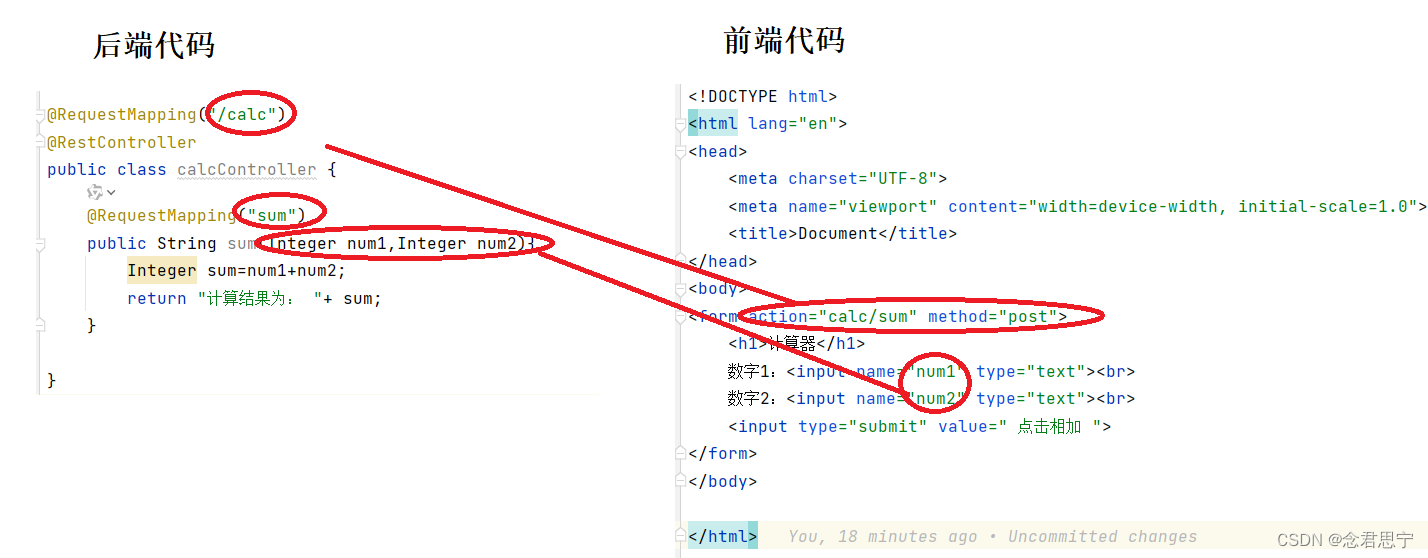
代码实现
from prettytable import PrettyTable
import numpy as np
import akshare as ak
from scipy.stats import genextreme as gev
from scipy.stats import genpareto as pot
# 利用akshare读取股票收益序列
stock = ak.stock_zh_a_hist(symbol='000001', period="daily", start_date="20071012", end_date='20081012', adjust="")
price = stock['收盘']
# GEV
c, loc, scale = gev.fit(price[price < np.percentile(price, 5)])
confidence_level = 0.95
VaR_gev = gev.ppf(confidence_level, c, loc, scale)
# POT
threshold = 17
choose = price[price < threshold]
c, beta, epsilon = pot.fit(choose)
n = float(len(price))
nu = float(len(choose))
VaR_POT = choose.mean() + beta/epsilon * ((n / nu * (confidence_level ** (-float(epsilon)))) - 1)
# print
VaR = PrettyTable(['Tool', 'VaR'])
VaR.add_row(['GEV', round(VaR_gev, 4)])
VaR.add_row(['POT', round(VaR_POT, 4)])
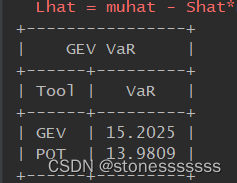
print(VaR.get_string(title="GEV VaR"))
输出结果:

![[CISCN2019 华北赛区 Day2 Web1]Hack World 1 题目分析与详解](https://img-blog.csdnimg.cn/direct/2cbd5b93d0114c1b94ab42ced97d86bd.png)