Triton 简介

• OpenAI 研发的 Triton 是一个专门为深度学习和高性能计算任务设计的编程语言和编译器，它旨在简化并优化在GPU上执行的复杂操作的开发。Triton 的目标是提供一个开源环境，以比 CUDA 更高的生产力编写快速代码。

• 官方资料

  • 官方代码：https://github.com/openai/triton
  • 官方文档：https://triton-lang.org/main/getting-started/installation.html

背景

• 传统的基于 CUDA 进行 GPU 编程难度较大，学术界和工业界都对面向 GPU 编程的领域特定语言（DSL）很感兴趣。但是目前已有的 DSL 在灵活性和（对相同算法）速度上明显慢于像 cuBLAS、cuDNN 或 TensorRT 这样的库中可用的最佳手写计算内核。已有的 DSL 如 polyhedral machinery (Tiramisu/Tensor Comprehensions)、scheduling languages (Halide、TVM) 等在效率上还有提升空间。
• Triton 被提出就是希望作为一个编写灵活的 DSL 来将低 GPU 编程难度的同时提升也提升算子效率

Triton 与 CUDA 的关系

• Triton 的核心理念是基于分块的编程范式可以促进神经网络的高性能计算核心的构建。CUDA 编写属于传统的 “单程序，多数据” GPU 执行模型，在线程的细粒度上进行编程，Triton 是在分块的细粒度上进行编程。例如，在矩阵乘法的情况下，CUDA和Triton有以下不同
  
  可以看出 triton 在循环中是逐块进行计算的。这种方法的一个关键优势是，它导致了块结构的迭代空间，相较于现有的DSL，为程序员在实现稀疏操作时提供了更多的灵活性，同时允许编译器为数据局部性和并行性进行积极的优化。

Triton 开发样例

样例一：Triton vector addition 算子

• 使用 Triton 编写一个简单的向量加法算子。学习以下内容：
  • Triton 的基本编程方式
  • triton.jit 装饰器使用方式，用于定义 Triton 内核
  • 与参考的 torch 算子进行测速对比的方式

Triton kernel 实现

import torch

import triton
import triton.language as tl

@triton.jit
def add_kernel(x_ptr,  # 第一个输入向量的指针。
               y_ptr,  # 第二个输入向量的指针。
               output_ptr,  # 输出向量的指针。
               n_elements,  # 向量的大小。
               BLOCK_SIZE: tl.constexpr,  # 每个程序应该处理的元素数量。
               # 注意：`constexpr` 可以作为形状值使用。
               ):
    # 有多个'程序'处理不同的数据。我们在这里标识我们是哪个程序：
    pid = tl.program_id(axis=0)  # 我们使用 1D launch 网格，因此 axis 是 0。
    # 该程序将处理与初始数据偏移的输入。
    # 例如，如果您有长度为 256 的向量和块大小为 64，程序
    # 将分别访问元素[0:64, 64:128, 128:192, 192:256]。
    # 请注意，偏移量是指针的列表：
    block_start = pid * BLOCK_SIZE
    offsets = block_start + tl.arange(0, BLOCK_SIZE)
    # 创建一个掩码以防止内存操作超出范围。
    mask = offsets < n_elements
    # 从 DRAM 加载 x 和 y，以掩盖掉输入不是块大小的倍数的任何额外元素。
    x = tl.load(x_ptr + offsets, mask=mask)
    y = tl.load(y_ptr + offsets, mask=mask)
    output = x + y
    # 将 x + y 写回到 DRAM。
    tl.store(output_ptr + offsets, output, mask=mask)

这段代码是一个用于执行向量加法的 Triton 内核定义，使用 @triton.jit 装饰器进行即时编译（JIT）以便在 GPU 上执行。它逐元素地将两个向量相加，并将结果存储在第三个向量中。

1. 输入和输出指针：x_ptr, y_ptr, 和 output_ptr 分别是指向第一个输入向量、第二个输入向量和输出向量的指针。这些向量存储在 GPU 的内存中。

2. 向量大小和块大小：n_elements 是向量中元素的总数。BLOCK_SIZE 是一个编译时常量（tl.constexpr），定义了每个 GPU 程序（或称为线程块）应该处理的元素数量。

3. 程序标识和数据偏移：通过 tl.program_id(axis=0) 获取当前程序（线程块）的唯一标识符 pid。然后，根据这个 ID 和块大小计算出这个程序负责处理的数据段的起始偏移量 block_start。每个程序负责处理一小块数据，这样可以并行处理整个向量。

4. 内存访问和掩码：offsets 计算每个元素在向量中的位置，mask 用于创建一个布尔掩码，以防止对数组界外的内存进行操作。这是必要的，因为向量的大小可能不是块大小的整数倍，导致最后一个程序块可能没有足够的元素来处理。

5. 加载、计算和存储：使用 tl.load 函数根据 offsets 和 mask 从输入向量中加载元素，执行加法操作得到 output，然后再使用 tl.store 将计算结果根据相同的 offsets 和 mask 存储回输出向量。

这种方法利用了 GPU 的并行计算能力，通过将数据分块并分配给多个程序（线程块）来加速向量加法操作。通过适当选择 BLOCK_SIZE，可以优化内核的性能，以适应特定的硬件和问题规模。

kernel 函数封装

• 声明一个辅助函数来（1）分配张量和（2）以适当的网格/块大小排队上述 kernel

def add(x: torch.Tensor, y: torch.Tensor):
    # 我们需要预先分配输出。
    output = torch.empty_like(x)
    assert x.is_cuda and y.is_cuda and output.is_cuda
    n_elements = output.numel()
    # SPMD启动网格表示并行运行的内核实例数。
    # 它类似于CUDA启动网格。它可以是Tuple[int]，或者是Callable(metaparameters) -> Tuple[int]。
    # 在这种情况下，我们使用一个1D网格，其大小是块的数量：
    grid = lambda meta: (triton.cdiv(n_elements, meta['BLOCK_SIZE']), )
    # 注意：
    #  - 每个torch.tensor对象都隐式地转换为指向其第一个元素的指针。
    #  - `triton.jit`'ed函数可以通过一个启动网格索引来获得一个可调用的GPU内核。
    #  - 不要忘记将元参数作为关键字参数传递。
    add_kernel[grid](x, y, output, n_elements, BLOCK_SIZE=1024)
    # 我们返回一个指向z的句柄，但是，由于`torch.cuda.synchronize()`尚未被调用，内核此时仍在异步运行。
    return output

定义了一个 Python 函数 add，用于准备数据、调用内核并管理 GPU 上的执行过程。

• 输出预分配和验证：函数开始时，先为输出向量 output 分配空间，确保输入和输出向量都位于 GPU 上。
• 计算启动网格：根据输入向量的元素数量 n_elements 和给定的块大小 BLOCK_SIZE，计算 Triton 启动网格的大小。这个网格决定了并行执行多少个内核实例。其中 triton.cdiv 是执行向上取整的整数除法。
• 内核调用：使用 add_kernel[grid] 语法调用 Triton 内核，传递输入向量、输出向量、元素数量和块大小等参数。这里使用了一个 lambda 函数来定义网格大小，确保网格是动态计算的。
• 异步执行：函数执行内核调用后立即返回输出向量的句柄。在这一点上，GPU 上的计算可能仍在异步执行。

函数调用

• 使用上述函数计算两个 torch.tensor 对象的逐元素和，并测试其正确性

torch.manual_seed(0)
size = 98432
x = torch.rand(size, device='cuda')
y = torch.rand(size, device='cuda')
output_torch = x + y
output_triton = add(x, y)
print(output_torch)
print(output_triton)
print(f'在torch和triton之间的最大差异是 '
      f'{torch.max(torch.abs(output_torch - output_triton))}')
# 输出
# tensor([1.3713, 1.3076, 0.4940,  ..., 0.6724, 1.2141, 0.9733], device='cuda:0')
# tensor([1.3713, 1.3076, 0.4940,  ..., 0.6724, 1.2141, 0.9733], device='cuda:0')
# 在torch和triton之间的最大差异是 0.0

triton 封装的 add 算子在 pytorch 代码中直接调用即可，注意输入 tensor 需要放在 GPU 上，triton 和 torch 的运行结果是完全一致的

性能测试

• 对逐渐增大的向量大小进行基准测试，以了解 Triton 实现相对于 PyTorch 的表现如何。为了简化操作，Triton 提供了一套内置工具，允许简洁地绘制自定义操作在不同向量大小下的性能图表。

@triton.testing.perf_report(
    triton.testing.Benchmark(
        x_names=['size'],  # 用作图表x轴的参数名。
        x_vals=[2**i for i in range(12, 28, 1)],  # `x_name`的不同可能值。
        x_log=True,  # x轴是对数的。
        line_arg='provider',  # 其值对应图表中不同线条的参数名。
        line_vals=['triton', 'torch'],  # `line_arg`的可能值。
        line_names=['Triton', 'Torch'],  # 线条的标签名。
        styles=[('blue', '-'), ('green', '-')],  # 线条样式。
        ylabel='GB/s',  # y轴的标签名。
        plot_name='vector-add-performance',  # 图表的名称。也用作保存图表的文件名。
        args={},  # 不在`x_names`和`y_name`中的函数参数值。
    ))
def benchmark(size, provider):
    x = torch.rand(size, device='cuda', dtype=torch.float32)
    y = torch.rand(size, device='cuda', dtype=torch.float32)
    quantiles = [0.5, 0.2, 0.8]
    if provider == 'torch':
        ms, min_ms, max_ms = triton.testing.do_bench(lambda: x + y, quantiles=quantiles)
    if provider == 'triton':
        ms, min_ms, max_ms = triton.testing.do_bench(lambda: add(x, y), quantiles=quantiles)
    gbps = lambda ms: 12 * size / ms * 1e-6
    return gbps(ms), gbps(max_ms), gbps(min_ms)

我们现在可以运行上面装饰过的函数得到测试结果，性能以 GB/s 为单位，这反映了操作的吞吐量：

benchmark.run(print_data=True, show_plots=True, save_path='./output')

• 测试结果对比
  

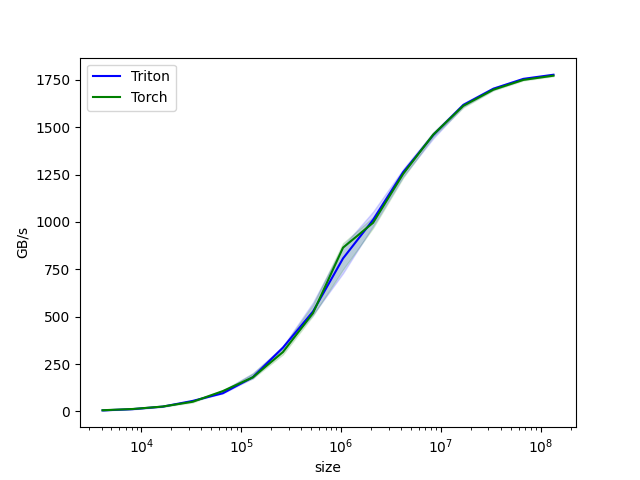
vector-add-performance:
           size       Triton        Torch
0        4096.0     5.545126     6.373444
1        8192.0    12.287999    12.934737
2       16384.0    25.440993    25.815125
3       32768.0    55.601811    51.200001
4       65536.0    96.000000   107.318778
5      131072.0   180.705879   180.043948
6      262144.0   336.657521   313.070059
7      524288.0   527.099213   518.754611
8     1048576.0   807.425031   864.210987
9     2097152.0  1010.838063   995.483519
10    4194304.0  1262.330599  1253.278078
11    8388608.0  1457.705349  1460.412186
12   16777216.0  1616.925188  1612.367029
13   33554432.0  1702.694469  1697.640561
14   67108864.0  1754.694212  1749.327388
15  134217728.0  1776.463251  1771.492650

样例二：融合 Softmax 算子

编写一个融合的 softmax 算子，对于特定类别的矩阵（行可以适配 GPU 的 SRAM 的矩阵）来说，这个操作比 PyTorch 的原生操作要快得多。本样例学习以下内容：

• 内核融合对于带宽受限操作的好处
• Triton 中的 Reduction 操作符

动机

自定义 GPU 内核用于逐元素加法在教育上是有价值的，但在实践中帮助不大。让我们考虑一个简单的（数值稳定的）softmax 操作的情况：

import torch
import triton
import triton.language as tl

@torch.jit.script
def naive_softmax(x):
    """使用原生 pytorch 计算 X 的逐行 softmax

    我们减去最大元素以避免溢出。Softmax 对这种位移是不变的。
    """
    # 读取 MN 个元素；写入 M 个元素
    x_max = x.max(dim=1)[0]
    # 读取 MN + M 个元素；写入 MN 个元素
    z = x - x_max[:, None]
    # 读取 MN 个元素；写入 MN 个元素
    numerator = torch.exp(z)
    # 读取 MN 个元素；写入 M 个元素
    denominator = numerator.sum(dim=1)
    # 读取 MN + M 个元素；写入 MN 个元素
    ret = numerator / denominator[:, None]
    # 总计：读取 5MN + 2M 个元素；写入 3MN + 2M 个元素
    return ret

当在 PyTorch 中以朴素方式实现时，计算 y = naive_softmax(x) 需要从 DRAM 读取 (5MN + 2M) 个元素，并写回 (3MN + 2M) 个元素。这显然是浪费的；我们更希望有一个自定义的“融合”内核，它只读取一次 X 并在芯片上完成所有必要的计算。这样做将只需要读取和写回 (MN + M) 元素，因此我们可以预期理论上的加速约为 ~4x（即，(5MN + 2M) 到 (MN + M)）。torch.jit.script 标志旨在自动执行这种“内核融合”，但正如我们稍后将看到的，它仍然远非理想。

Triton kernel 实现

• softmax 内核的工作原理如下：每个程序加载输入矩阵 X 的一行，对其进行标准化，然后将结果写回输出 Y。

请注意，Triton 的一个重要限制是每个块必须具有 2 的幂个元素，因此如果我们想处理任何可能的输入形状，我们需要在内部对每行进行“填充”并正确保护内存操作：

@triton.jit
def softmax_kernel(output_ptr, input_ptr, input_row_stride, output_row_stride, n_cols, BLOCK_SIZE: tl.constexpr):
    # softmax 的行是独立的，所以我们在这些行上并行化
    row_idx = tl.program_id(0)
    # 步长表示我们需要增加指针的数量以前进1行
    row_start_ptr = input_ptr + row_idx * input_row_stride
    # 块大小是大于 n_cols 的下一个2的幂，这样我们可以将每
    # 行适配在单个块中
    col_offsets = tl.arange(0, BLOCK_SIZE)
    input_ptrs = row_start_ptr + col_offsets
    # 使用掩码将行加载到SRAM中，因为 BLOCK_SIZE 可能大于 n_cols
    row = tl.load(input_ptrs, mask=col_offsets < n_cols, other=-float('inf'))
    # 减去最大值以保证数值稳定性
    row_minus_max = row - tl.max(row, axis=0)
    # 注意，在 Triton 中指数运算是快速但近似的（即，想象在 CUDA 中的 __expf）
    numerator = tl.exp(row_minus_max)
    denominator = tl.sum(numerator, axis=0)
    softmax_output = numerator / denominator
    # 将输出写回到 DRAM
    output_row_start_ptr = output_ptr + row_idx * output_row_stride
    output_ptrs = output_row_start_ptr + col_offsets
    tl.store(output_ptrs, softmax_output, mask=col_offsets < n_cols)

kernel 封装

• 我们可以创建一个辅助函数，为任何给定的输入张量排队内核及其（元）参数。

def softmax(x):
    n_rows, n_cols = x.shape
    # 块大小是大于 `x` 中列数的最小2的幂
    BLOCK_SIZE = triton.next_power_of_2(n_cols)
    # 另一个我们可以使用的技巧是要求编译器通过
    # 增加每行分布的 warps 数量（`num_warps`）来使用更多线程。
    # 在下一个教程中，你将看到如何以更自然的方式自动调整这个值，
    # 这样你就不必自己提出手工启发式方法。
    num_warps = 4
    if BLOCK_SIZE >= 2048:
        num_warps = 8
    if BLOCK_SIZE >= 4096:
        num_warps = 16
    # 分配输出
    y = torch.empty_like(x)
    # 排队内核。1D启动网格很简单：输入矩阵的每一行分配一个 kernel 实例
    softmax_kernel[(n_rows, )](
        y,
        x,
        x.stride(0),
        y.stride(0),
        n_cols,
        num_warps=num_warps,
        BLOCK_SIZE=BLOCK_SIZE,
    )
    return y

triton.next_power_of_2 计算并返回大于或等于给定数字的最小的 2 的幂。这个函数在 GPU 编程中特别有用，尤其是在需要将数据大小调整为 2 的幂以优化内存访问和并行计算性能时。

单元测试

• 我们确保在具有不规则行和列数的矩阵上测试我们的内核。这将使我们能够验证我们的填充机制是否有效。

torch.manual_seed(0)
x = torch.randn(1823, 781, device='cuda')
y_triton = softmax(x)
y_torch = torch.softmax(x, axis=1)
assert torch.allclose(y_triton, y_torch), (y_triton, y_torch)

正如预期，结果是一致的。

性能测试

• 将根据输入矩阵中的列数对我们的操作进行性能测试——假设有 4096 行。然后，我们将其性能与（1）torch.softmax 和（2）上面定义的 naive_softmax 进行比较

@triton.testing.perf_report(
    triton.testing.Benchmark(
        x_names=['N'],  # 用作图表x轴的参数名
        x_vals=[128 * i for i in range(2, 100)],  # `x_name`的不同可能值
        line_arg='provider',  # 其值对应图表中不同线条的参数名
        line_vals=[
            'triton',
            'torch-native',
            'torch-jit',
        ],  # `line_arg`的可能值
        line_names=[
            "Triton",
            "Torch (native)",
            "Torch (jit)",
        ],  # 线条的标签名
        styles=[('blue', '-'), ('green', '-'), ('green', '--')],  # 线条样式
        ylabel="GB/s",  # y轴的标签名
        plot_name="softmax-performance",  # 图表的名称。也用作保存图表的文件名。
        args={'M': 4096},  # 不在`x_names`和`y_name`中的函数参数值
    ))
def benchmark(M, N, provider):
    x = torch.randn(M, N, device='cuda', dtype=torch.float32)
    quantiles = [0.5, 0.2, 0.8]
    if provider == 'torch-native':
        ms, min_ms, max_ms = triton.testing.do_bench(lambda: torch.softmax(x, axis=-1), quantiles=quantiles)
    if provider == 'triton':
        ms, min_ms, max_ms = triton.testing.do_bench(lambda: softmax(x), quantiles=quantiles)
    if provider == 'torch-jit':
        ms, min_ms, max_ms = triton.testing.do_bench(lambda: naive_softmax(x), quantiles=quantiles)
    gbps = lambda ms: 2 * x.nelement() * x.element_size() * 1e-9 / (ms * 1e-3)
    return gbps(ms), gbps(max_ms), gbps(min_ms)


benchmark.run(show_plots=True, print_data=True)

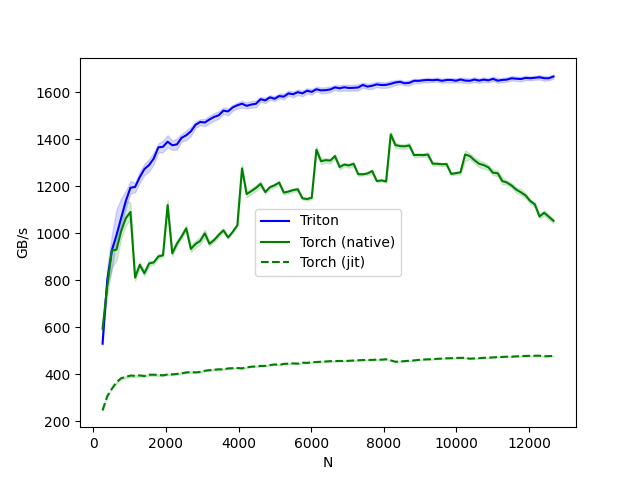
• triton 的吞吐是显著高于原生 torch 的。
  • Triton 比 Torch JIT 快 4 倍。这证实了我们的怀疑，即 Torch JIT 在这里没有进行任何融合操作。
  • Triton 明显比 torch.softmax 快。然而请注意，PyTorch 的 softmax 操作更通用，可以在任何形状的张量上工作。

softmax-performance:
          N       Triton  Torch (native)  Torch (jit)
0     256.0   529.583854      593.085987   245.683230
1     384.0   797.598331      772.526559   305.291919
2     512.0   926.303883      925.486309   337.596920
3     640.0   991.467433      929.588635   365.510311
4     768.0  1064.184060     1008.246151   382.691962
..      ...          ...             ...          ...
93  12160.0  1660.909688     1121.686333   478.199613
94  12288.0  1663.196305     1070.749440   478.510479
95  12416.0  1658.922723     1086.479561   475.751543
96  12544.0  1658.817810     1069.619083   476.837796
97  12672.0  1666.276460     1052.360210   476.818108

样例三：矩阵乘算子 (Matrix Multiplication)

编写一个非常简短的高性能 FP16 矩阵乘法内核，其性能与 cuBLAS 相当。具体学习以下内容：

• 块级矩阵乘法。
• 多维指针算术。
• 程序重排以提高 L2 缓存命中率。
• 自动性能调优。

动机

• 矩阵乘法是大多数现代高性能计算系统的关键构建块。它们是出了名的难以优化，因此它们的实现通常由硬件供应商自己作为所谓的“内核库”的一部分来完成（例如，cuBLAS）。不幸的是，这些库通常是专有的，不能轻易地定制以适应现代深度学习工作负载的需求（例如，融合激活函数）。用 Triton 自己实现高效的矩阵乘法的方式易于定制和扩展。
• 大致来说，编写的 Triton 内核将实现以下 block 算法来将一个 (M, K) 乘以一个 (K, N) 矩阵：

# 并行执行
for m in range(0, M, BLOCK_SIZE_M):
  # 并行执行
  for n in range(0, N, BLOCK_SIZE_N):
    acc = zeros((BLOCK_SIZE_M, BLOCK_SIZE_N), dtype=float32)
    for k in range(0, K, BLOCK_SIZE_K):
      a = A[m : m+BLOCK_SIZE_M, k : k+BLOCK_SIZE_K]
      b = B[k : k+BLOCK_SIZE_K, n : n+BLOCK_SIZE_N]
      acc += dot(a, b)
    C[m : m+BLOCK_SIZE_M, n : n+BLOCK_SIZE_N] = acc

其中，双重嵌套 for 循环的每次迭代都由一个专门的 Triton 程序实例执行。

Triton kernel

上述算法实际上在 Triton 中实现起来相当直接。主要的难点来自于在内循环中计算读取 A 和 B 块的内存位置。为此，我们需要多维指针运算。

• 指针运算
  对于一个行主序的 2D 张量 X，X[i, j] 的内存位置由 &X[i, j] = X + i*stride_xi + j*stride_xj 给出。因此，可以用伪代码定义 A[m : m+BLOCK_SIZE_M, k:k+BLOCK_SIZE_K] 和 B[k : k+BLOCK_SIZE_K, n : n+BLOCK_SIZE_N] 的指针块如下：

&A[m : m+BLOCK_SIZE_M, k:k+BLOCK_SIZE_K] = a_ptr + (m : m+BLOCK_SIZE_M)[:, None]*A.stride(0) + (k : k+BLOCK_SIZE_K)[None, :]*A.stride(1);
&B[k : k+BLOCK_SIZE_K, n:n+BLOCK_SIZE_N] = b_ptr + (k : k+BLOCK_SIZE_K)[:, None]*B.stride(0) + (n : n+BLOCK_SIZE_N)[None, :]*B.stride(1);

这意味着 A 和 B 的块指针可以在 Triton 中初始化（即，k=0），代码如下。还要注意，我们需要一个额外的模运算来处理 M 不是 BLOCK_SIZE_M 的倍数或 N 不是 BLOCK_SIZE_N 的倍数的情况，在这种情况下，我们可以用一些无用的值填充数据，这些值不会对结果产生贡献。对于 K 维度，我们稍后将使用掩码加载语义来处理。

offs_am = (pid_m * BLOCK_SIZE_M + tl.arange(0, BLOCK_SIZE_M)) % M
offs_bn = (pid_n * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)) % N
offs_k = tl.arange(0, BLOCK_SIZE_K)
a_ptrs = a_ptr + (offs_am[:, None]*stride_am + offs_k [None, :]*stride_ak)
b_ptrs = b_ptr + (offs_k [:, None]*stride_bk + offs_bn[None, :]*stride_bn)

然后在内循环中如下更新：

a_ptrs += BLOCK_SIZE_K * stride_ak;
b_ptrs += BLOCK_SIZE_K * stride_bk;

L2缓存优化

如上所述，每个程序实例计算一个 [C_BLOCK_SIZE_M, C_BLOCK_SIZE_N] 的 C 块。重要的是要记住，这些块的计算顺序很重要，因为它会影响我们程序的 L2 缓存命中率，不幸的是，简单的行主序排序

pid = triton.program_id(0);
grid_m = (M + BLOCK_SIZE_M - 1) // BLOCK_SIZE_M;
grid_n = (N + BLOCK_SIZE_N - 1) // BLOCK_SIZE_N;
pid_m = pid / grid_n;
pid_n = pid % grid_n;

就是不够的。

一种可能的解决方案是按照促进数据重用的顺序启动块。这可以通过在转到下一列之前，将块在 GROUP_M 行的组中进行‘超级分组’来完成：

# 程序ID
pid = tl.program_id(axis=0)
# 沿M轴的程序ID数量
num_pid_m = tl.cdiv(M, BLOCK_SIZE_M)
# 沿N轴的程序ID数量
num_pid_n = tl.cdiv(N, BLOCK_SIZE_N)
# 组中的程序数量
num_pid_in_group = GROUP_SIZE_M * num_pid_n
# 此程序所在组的ID
group_id = pid // num_pid_in_group
# 组中第一个程序的行ID
first_pid_m = group_id * GROUP_SIZE_M
# 如果`num_pid_m`不能被`GROUP_SIZE_M`整除，最后一个组会更小
group_size_m = min(num_pid_m - first_pid_m, GROUP_SIZE_M)
# *在组内*，程序按列主序排列
# 程序在*启动网格*中的行ID
pid_m = first_pid_m + (pid % group_size_m)
# 程序在*启动网格*中的列ID
pid_n = (pid % num_pid_in_group) // group_size_m

例如，在下面的矩阵乘法中，每个矩阵是 9 块乘以 9 块，我们可以看到，如果我们按行主序计算输出，我们需要加载 90 个块到 SRAM 以计算前 9 个输出块，但如果我们按分组顺序做，我们只需要加载 54 个块。

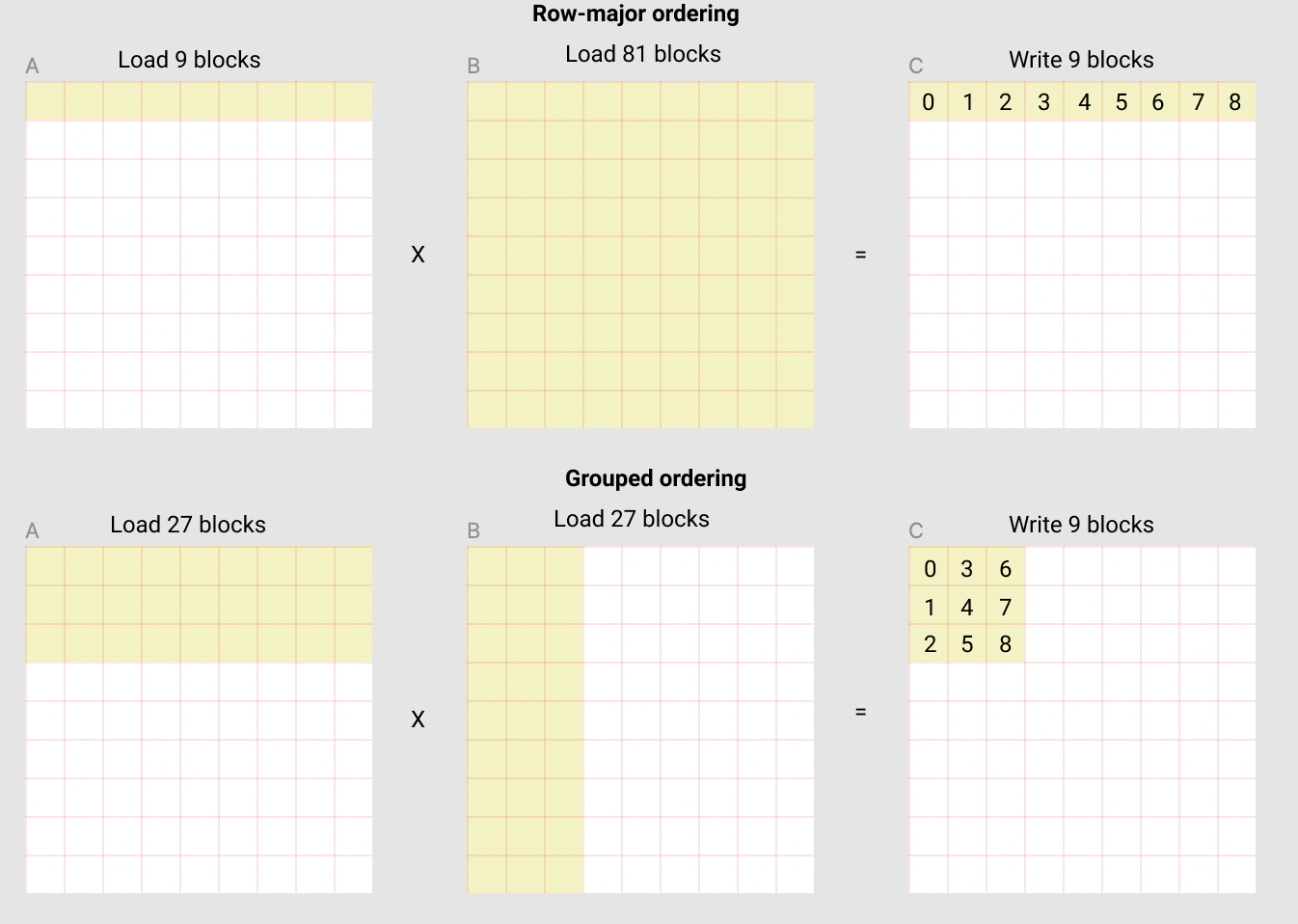
实际上，这可以在某些硬件架构上（例如，在A100上从 220 提高到 245 TFLOPS）将我们的矩阵乘法核心的性能提高 10% 以上。

kernel 实现

import torch
import triton
import triton.language as tl

# 可以通过使用`triton.autotune`装饰器自动调优被`triton.jit`修饰的函数，它接收：
#   - 一系列`triton.Config`对象，定义了不同配置的
#       元参数（例如，`BLOCK_SIZE_M`）和编译选项（例如，`num_warps`）来尝试
#   - 一个自动调优*关键字*，其值的变化将触发所有
#       提供的配置的评估
@triton.autotune(
    configs=[
        triton.Config({'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 256, 'BLOCK_SIZE_K': 64, 'GROUP_SIZE_M': 8}, num_stages=3, num_warps=8),
        triton.Config({'BLOCK_SIZE_M': 64, 'BLOCK_SIZE_N': 256, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8}, num_stages=4, num_warps=4),
        triton.Config({'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 128, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8}, num_stages=4, num_warps=4),
        triton.Config({'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 64, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8}, num_stages=4, num_warps=4),
        triton.Config({'BLOCK_SIZE_M': 64, 'BLOCK_SIZE_N': 128, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8}, num_stages=4, num_warps=4),
        triton.Config({'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 32, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8}, num_stages=4, num_warps=4),
        triton.Config({'BLOCK_SIZE_M': 64, 'BLOCK_SIZE_N': 32, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8}, num_stages=5, num_warps=2),
        triton.Config({'BLOCK_SIZE_M': 32, 'BLOCK_SIZE_N': 64, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8}, num_stages=5, num_warps=2),
    ],
    key=['M', 'N', 'K'],
)
@triton.jit
def matmul_kernel(
        a_ptr, b_ptr, c_ptr,
        M, N, K,
        stride_am, stride_ak,
        stride_bk, stride_bn,
        stride_cm, stride_cn,
        BLOCK_SIZE_M: tl.constexpr, BLOCK_SIZE_N: tl.constexpr, BLOCK_SIZE_K: tl.constexpr,
        GROUP_SIZE_M: tl.constexpr,
        ACTIVATION: tl.constexpr
):
    """用于计算矩阵乘法C = A x B的内核。
    A的形状为(M, K)，B的形状为(K, N)且C的形状为(M, N)
    """
    # 映射程序id `pid`到它应该计算的C块。
    # 这是通过分组排序完成的，以促进L2数据重用。
    # 详见上方`L2缓存优化`部分。
    pid = tl.program_id(axis=0)
    num_pid_m = tl.cdiv(M, BLOCK_SIZE_M)
    num_pid_n = tl.cdiv(N, BLOCK_SIZE_N)
    num_pid_in_group = GROUP_SIZE_M * num_pid_n
    group_id = pid // num_pid_in_group
    first_pid_m = group_id * GROUP_SIZE_M
    group_size_m = min(num_pid_m - first_pid_m, GROUP_SIZE_M)
    pid_m = first_pid_m + (pid % group_size_m)
    pid_n = (pid % num_pid_in_group) // group_size_m

    # 为A和B的第一个块创建指针。
    # 我们将在K方向移动时推进这个指针并累加
    offs_am = (pid_m * BLOCK_SIZE_M + tl.arange(0, BLOCK_SIZE_M)) % M
    offs_bn = (pid_n * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)) % N
    offs_k = tl.arange(0, BLOCK_SIZE_K)
    a_ptrs = a_ptr + (offs_am[:, None] * stride_am + offs_k[None, :] * stride_ak)
    b_ptrs = b_ptr + (offs_k[:, None] * stride_bk + offs_bn[None, :] * stride_bn)

    # 迭代计算C矩阵的一个块。
    accumulator = tl.zeros((BLOCK_SIZE_M, BLOCK_SIZE_N), dtype=tl.float32)
    for k in range(0, tl.cdiv(K, BLOCK_SIZE_K)):
        a = tl.load(a_ptrs, mask=offs_k[None, :] < K - k * BLOCK_SIZE_K, other=0.0)
        b = tl.load(b_ptrs, mask=offs_k[:, None] < K - k * BLOCK_SIZE_K, other=0.0)
        accumulator += tl.dot(a, b)
        a_ptrs += BLOCK_SIZE_K * stride_ak
        b_ptrs += BLOCK_SIZE_K * stride_bk
    if ACTIVATION == "leaky_relu":
        accumulator = leaky_relu(accumulator)
    c = accumulator.to(tl.float16)

    offs_cm = pid_m * BLOCK_SIZE_M + tl.arange(0, BLOCK_SIZE_M)
    offs_cn = pid_n * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)
    c_ptrs = c_ptr + stride_cm * offs_cm[:, None] + stride_cn * offs_cn[None, :]
    c_mask = (offs_cm[:, None] < M) & (offs_cn[None, :] < N)
    tl.store(c_ptrs, c, mask=c_mask)

@triton.jit
def leaky_relu(x):
    x = x + 1
    return tl.where(x >= 0, x, 0.01 * x)

kernel 封装

def matmul(a, b, activation=""):
    # 检查约束。
    assert a.shape[1] == b.shape[0], "维度符合矩阵相乘要求"
    assert a.is_contiguous(), "矩阵A必须是连续的"
    assert b.is_contiguous(), "矩阵B必须是连续的"
    M, K = a.shape
    K, N = b.shape
    # 分配输出。
    c = torch.empty((M, N), device=a.device, dtype=a.dtype)
    # 1D启动内核，每个块获得自己的程序。
    grid = lambda META: (triton.cdiv(M, META['BLOCK_SIZE_M']) * triton.cdiv(N, META['BLOCK_SIZE_N']), )
    matmul_kernel[grid](
        a, b, c,
        M, N, K,
        a.stride(0), a.stride(1),
        b.stride(0), b.stride(1),
        c.stride(0), c.stride(1),
        ACTIVATION=activation
    )
    return c

正确性测试

将自定义的矩阵乘法操作与原生的torch实现（即cuBLAS）进行比较。

torch.manual_seed(0)
a = torch.randn((512, 512), device='cuda', dtype=torch.float16)
b = torch.randn((512, 512), device='cuda', dtype=torch.float16)
triton_output = matmul(a, b)
torch_output = torch.matmul(a, b)
print(f"triton_output={triton_output}")
print(f"torch_output={torch_output}")
if torch.allclose(triton_output, torch_output, atol=1e-2, rtol=0):
    print("✅ Triton和Torch匹配")
else:
    print("❌ Triton和Torch不匹配")

这段代码首先使用 Triton 和 Torch 分别计算了两个随机生成的 16 位浮点格式的 512x512 矩阵 A 和 B 的乘积。然后，它比较了 Triton 和 Torch 的输出结果，如果两者足够接近（使用torch.allclose函数，绝对容差设为 1e-2），则认为两种实现匹配。

性能测试

比较 triton 的内核与 cuBLAS 的性能。这里我们关注的是方阵，也可以随意调整这个脚本来基准测试任何其他矩阵形状。

@triton.testing.perf_report(
    triton.testing.Benchmark(
        x_names=['M', 'N', 'K'],  # 用作图表x轴的参数名
        x_vals=[128 * i for i in range(2, 33)],  # `x_name`的不同可能值
        line_arg='provider',  # 对应于图表中不同线条的参数名
        line_vals=['cublas', 'triton'],  # `line_arg`的可能值
        line_names=["cuBLAS", "Triton"],  # 线条的标签名
        styles=[('green', '-'), ('blue', '-')],  # 线条样式
        ylabel="TFLOPS",  # y轴的标签名
        plot_name="matmul-performance",  # 图表的名称，也用作保存图表的文件名
        args={},  # 其他参数
    )
)
def benchmark(M, N, K, provider):
    a = torch.randn((M, K), device='cuda', dtype=torch.float16)
    b = torch.randn((K, N), device='cuda', dtype=torch.float16)
    quantiles = [0.5, 0.2, 0.8]
    if provider == 'cublas':
        ms, min_ms, max_ms = triton.testing.do_bench(lambda: torch.matmul(a, b), quantiles=quantiles)
    if provider == 'triton':
        ms, min_ms, max_ms = triton.testing.do_bench(lambda: matmul(a, b), quantiles=quantiles)
    perf = lambda ms: 2 * M * N * K * 1e-12 / (ms * 1e-3)
    return perf(ms), perf(max_ms), perf(min_ms)

benchmark.run(show_plots=True, print_data=True)

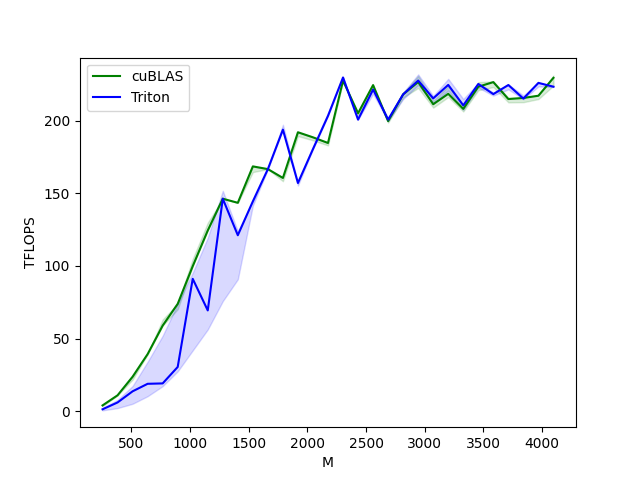
这段代码使用 triton.testing.perf_report 装饰器和 triton.testing.Benchmark 类设置和运行性能基准测试。它测试了不同大小的方阵乘法的性能，并比较了使用 cuBLAS 和 Triton 实现的性能。每个测试通过执行相应的矩阵乘法操作并测量执行时间来完成，然后根据这些时间计算并报告 TFLOPS（每秒万亿次浮点运算）性能指标。以下结果显示 Triton 的吞吐和 cuBLAS 接近：

matmul-performance:
         M       N       K      cuBLAS      Triton
0    256.0   256.0   256.0    4.096000    1.424696
1    384.0   384.0   384.0   11.059200    6.144000
2    512.0   512.0   512.0   23.831273   13.797053
3    640.0   640.0   640.0   39.384616   18.962963
4    768.0   768.0   768.0   58.982401   19.233391
5    896.0   896.0   896.0   73.943582   30.541912
6   1024.0  1024.0  1024.0   99.864382   91.180520
7   1152.0  1152.0  1152.0  124.415996   69.441488
8   1280.0  1280.0  1280.0  146.285712  146.285712
9   1408.0  1408.0  1408.0  143.467796  121.150576
10  1536.0  1536.0  1536.0  168.521144  144.446699
11  1664.0  1664.0  1664.0  166.646518  166.646518
12  1792.0  1792.0  1792.0  160.563196  193.783168
13  1920.0  1920.0  1920.0  191.999993  157.090908
14  2048.0  2048.0  2048.0  188.508043  180.400167
15  2176.0  2176.0  2176.0  184.620623  203.269178
16  2304.0  2304.0  2304.0  227.503545  229.691080
17  2432.0  2432.0  2432.0  205.069087  200.674737
18  2560.0  2560.0  2560.0  224.438347  221.405396
19  2688.0  2688.0  2688.0  199.647657  200.704002
20  2816.0  2816.0  2816.0  218.071046  218.071046
21  2944.0  2944.0  2944.0  226.527416  227.561796
22  3072.0  3072.0  3072.0  211.280236  215.296978
23  3200.0  3200.0  3200.0  218.430042  224.561413
24  3328.0  3328.0  3328.0  208.067338  210.500857
25  3456.0  3456.0  3456.0  223.328435  225.199917
26  3584.0  3584.0  3584.0  226.487136  218.241246
27  3712.0  3712.0  3712.0  214.833002  224.488407
28  3840.0  3840.0  3840.0  215.578945  215.159527
29  3968.0  3968.0  3968.0  217.124452  225.970261
30  4096.0  4096.0  4096.0  229.432024  223.324015

总结

• Triton 提供了一种类似于 Python 的编程接口，使得开发人员可以更容易地编写 GPU 加速代码，而无需深入了解 CUDA 编程
  • 注：虽然 Triton 简化了 GPU 编程，但了解基本的 GPU 架构和并行计算原理仍然非常重要。
• 通过自动优化执行配置，Triton 能够在不同的硬件上实现接近或超过手写 CUDA 代码的性能。