关于我为什么要写单独开一篇文章写二分,实际上那么多困难的算法,比如线段树,并查集等等都没有难倒我,我最近却被二分难倒了,而且是两次,两次在赛场上做不出来二分的应用题,于是我决定写一篇二分查找的算法总结.刚接触算法的时候本来是要写一篇的,但后面因为各种原因搁置了,现在来补一篇.我学的二分查找和传统的二分查找有一定的差别.传统的是将l和r都集中在一个点,这样非常不好处理边界.我学的二分查找会把l和r处理成相邻的两个元素.看下图.
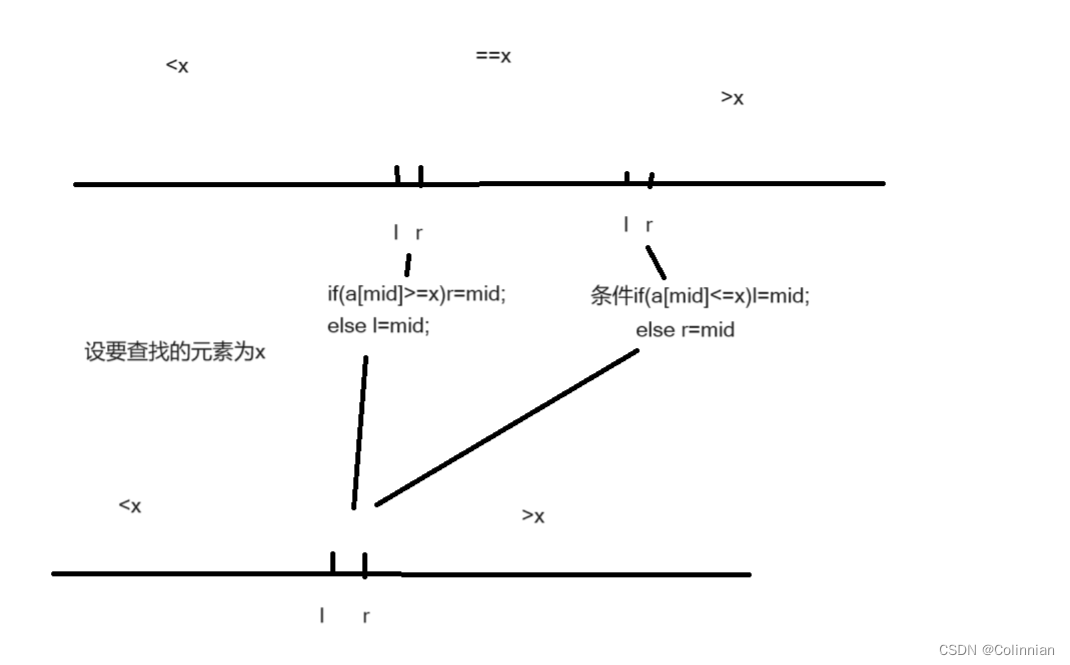
一种是中间有相等元素的情况,一种的没有的情况,两个条件对于第一种会通向各自所属情况,这也很好理解,对于第一种,如果mid>=x,你把它赋值给r,那就说明r最后所属元素肯定时>=x,而l是<x,它们最终会出现在各自的边界.这个问题解决了,我们来看while循环里该填什么条件,实际上应该填l+1<r,最终如果l+1==r了就不再进行查找了,说明已经找到边界了.
那最初的边界l和r应该怎么定义呢,我们先考虑一种特殊情况,假如<x或>x不存在,l和r该指向哪,对于第一种l是不是指向第一个元素的左边呀,r指向第一个元素,应为没有mid能赋给l,既然l会出现在第一个元素的左边,那我们定义边界的时候是不是也要让它为第一个元素的左边?同理r要定义为最右边的元素的右边一个,宽泛来讲,l定义为要查找范围最左边元素的左边一个元素,r为要查找范围的最右边的元素的右边一个.
总结一下
1.while(),括号里填l+1<r.
2.查找第一个大于等于x的,使用if(a[mid]>=x)r=mid;else l=mid.反之见上面的图(懒).
3.边界定义:l定义为要查找范围最左边元素的左边一个元素,r为要查找范围的最右边的元素的右边一个.
对于基础练习,这边建议刷一下洛谷的二分题单,还是很简单的【算法1-6】二分查找与二分答案 - 题单 - 洛谷
下面我主要想讲一下卡了我的一道div3的E题题
Problem - E - Codeforces
没做出来真羞耻啊
using i64 = long long;
using ll = long long;
i64 calc(int u, int x) {
//x个跑道,相当于u,u-1,u-2...u-x+1,总共有x个,那不就是倒序相加公式嘛
return 1LL * (u + u - x + 1) * x / 2;
}
void solve() {
ll n;
std::cin >> n;
std::vector<ll>a(n), b(n + 1);
//维护前缀和
for (int i = 0; i < n; i++) {
std::cin >> a[i];
b[i + 1] = b[i] + a[i];
}
ll q, l, u;
std::cin >> q;
std::vector<ll>bns;
while (q--) {
std::cin >> l >> u;
u;
//前面说的边界问题,找l到n,边界定义为l-1,n+1
l--;
ll k = l, j = n + 1;
while (l + 1 < j) {
ll mid = (l + j) / 2;
if (b[mid] < b[k] + u)l = mid;
else j = mid;
}
i64 ans = -1E18;
int r = -1;
//右边界小于等于n
if (j <= n) {
if (calc(u, b[j] - b[k]) > ans) {
ans = calc(u, b[j] - b[k]);
r = j;
}
}
//j左边是l,l=j-1,k是l-1,l不能等于k-1,所以j-1>k
if (j-1>k) {
if (calc(u, b[j - 1] - b[k]) >= ans) {
ans = calc(u, b[j - 1] - b[l]);
r = j - 1;
}
}
bns.push_back(r);
}
//其实你可以直接打印,没必要像我一样先存数组里.
for (int i = 0; i < bns.size(); i++)std::cout << bns[i] << ' ';
std::cout << '\n';
}
int main() {
std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);
int t;
std::cin >> t;
while (t--) {
solve();
}
return 0;
}实际上把边界处理好这道题还是很简单的,怪我太笨了.