深度学习精选笔记（8）梯度消失和梯度爆炸

news2024/11/20 15:36:54

学习参考：

动手学深度学习2.0
Deep-Learning-with-TensorFlow-book
pytorchlightning

①如有冒犯、请联系侵删。
②已写完的笔记文章会不定时一直修订修改(删、改、增)，以达到集多方教程的精华于一文的目的。
③非常推荐上面（学习参考）的前两个教程，在网上是开源免费的，写的很棒，不管是开始学还是复习巩固都很不错的。

深度学习回顾，专栏内容来源多个书籍笔记、在线笔记、以及自己的感想、想法，佛系更新。争取内容全面而不失重点。完结时间到了也会一直更新下去，已写完的笔记文章会不定时一直修订修改(删、改、增)，以达到集多方教程的精华于一文的目的。所有文章涉及的教程都会写在开头、一起学习一起进步。

一、数值稳定性的重要性

到目前为止，实现的每个模型都是根据某个预先指定的分布来初始化模型的参数。

有人会认为初始化方案是理所当然的，忽略了如何做出这些选择的细节。甚至有人可能会觉得，初始化方案的选择并不是特别重要。

相反，初始化方案的选择在神经网络学习中起着举足轻重的作用，它对保持数值稳定性至关重要。此外，这些初始化方案的选择可以与非线性激活函数的选择有趣的结合在一起。 选择哪个函数以及如何初始化参数可以决定优化算法收敛的速度有多快。糟糕选择可能会导致我们在训练时遇到梯度爆炸或梯度消失。

考虑一个具有 𝐿 层、输入 𝐱和输出 𝐨的深层网络。每一层 𝑙由变换 𝑓𝑙定义，该变换的参数为权重 𝐖(𝑙) ，其隐藏变量是 𝐡(𝑙)（令 𝐡(0)=𝐱）。网络可以表示为：
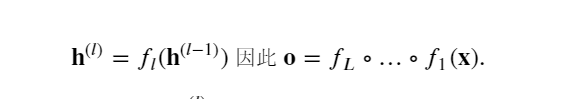
在这里插入图片描述
如果所有隐藏变量和输入都是向量，可以将 𝐨关于任何一组参数 𝐖(𝑙) 的梯度写为下式，该梯度是 𝐿−𝑙 个矩阵 𝐌(𝐿)⋅…⋅𝐌(𝑙+1) 与梯度向量 𝐯(𝑙) 的乘积。

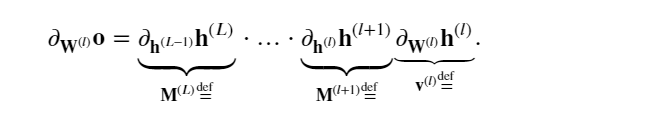
因此，上面公式计算的结果容易受到数值下溢问题的影响. 当将太多的概率乘在一起时，这些问题经常会出现。在处理概率时，一个常见的技巧是切换到对数空间，即将数值表示的压力从尾数转移到指数。不幸的是，上面的问题更为严重：最初，矩阵 𝐌(𝑙) 可能具有各种各样的特征值。他们可能很小，也可能很大；他们的乘积可能非常大，也可能非常小。

不稳定梯度带来的风险不止在于数值表示；不稳定梯度也威胁到优化算法的稳定性。

可能面临一些问题：

梯度爆炸（gradient exploding）问题：参数更新过大，破坏了模型的稳定收敛；
梯度消失（gradient vanishing）问题：参数更新过小，在每次更新时几乎不会移动，导致模型无法学习。

二、梯度消失

在深度神经网络中，梯度消失指的是在反向传播过程中，梯度逐渐变小并接近零，导致较深层的网络参数无法得到有效更新，从而影响模型的训练效果。

梯度消失通常发生在使用激活函数导数具有较小值的情况下，尤其是在使用 sigmoid 或 tanh 激活函数时。

sigmoid函数 1/(1+exp(−𝑥))很流行，因为它类似于阈值函数。由于早期的人工神经网络受到生物神经网络的启发，神经元要么完全激活要么完全不激活（就像生物神经元）的想法很有吸引力。然而，它却是导致梯度消失问题的一个常见的原因。下图是sigmoid函数变化图和梯度变化图。

%matplotlib inline
import tensorflow as tf
from d2l import tensorflow as d2l

x = tf.Variable(tf.range(-8.0, 8.0, 0.1))
with tf.GradientTape() as t:
    y = tf.nn.sigmoid(x)
d2l.plot(x.numpy(), [y.numpy(), t.gradient(y, x).numpy()],
         legend=['sigmoid', 'gradient'], figsize=(4.5, 2.5))

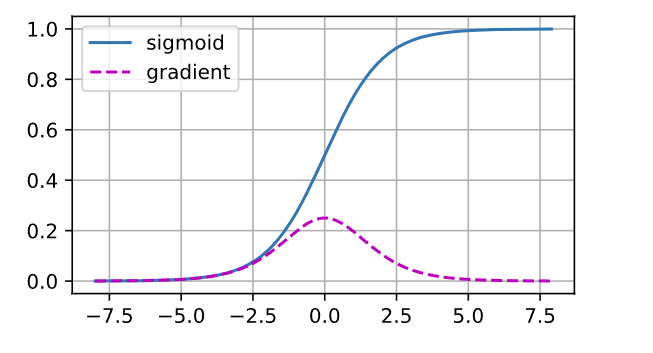
在这里插入图片描述
当sigmoid函数的输入很大或是很小时，它的梯度都会消失。此外，当反向传播通过许多层时，除非在刚刚好的地方，这些地方sigmoid函数的输入接近于零，否则整个乘积的梯度可能会消失。当网络有很多层时，除非很小心，否则在某一层可能会切断梯度。

事实上，这个问题曾经困扰着深度网络的训练。因此，更稳定的ReLU系列函数已经成为从业者的默认选择（虽然在神经科学的角度看起来不太合理）。

三、梯度爆炸

梯度爆炸则是指在反向传播过程中，梯度变得非常大，超过了数值范围，导致参数更新过大，模型无法稳定训练。

梯度爆炸通常出现在网络层数较多、权重初始化不当或者学习率设置过高的情况下。

相反，梯度爆炸可能同样令人烦恼。为了更好地说明这一点，生成100个高斯随机矩阵，并将它们与某个初始矩阵相乘。对于我们选择的尺度（方差 𝜎²=1 ），矩阵乘积发生爆炸。当这种情况是由于深度网络的初始化所导致时，导致没有机会让梯度下降优化器收敛。

M = tf.random.normal((4, 4))
print('一个矩阵 \n', M)
for i in range(100):
    M = tf.matmul(M, tf.random.normal((4, 4)))

print('乘以100个矩阵后\n', M.numpy())

一个矩阵 
 tf.Tensor(
[[ 3.7436965   2.652792    0.5994665  -0.17366047]
 [ 0.6720035  -0.7297903   0.3705189  -0.5043682 ]
 [ 0.53814566 -0.94948226  0.09689955 -0.4441989 ]
 [ 0.6737587   0.41651404 -0.9230542   0.1903977 ]], shape=(4, 4), dtype=float32)
乘以100个矩阵后
 [[-1.9263415e+26  1.5658991e+27  3.4174752e+26 -9.1476850e+25]
 [ 1.4916346e+24 -1.2148971e+25 -2.6495698e+24  7.0983965e+23]
 [ 2.5503458e+25 -2.0726612e+26 -4.5202026e+25  1.2112884e+25]
 [ 1.2258523e+25 -9.9649782e+25 -2.1730161e+25  5.8238054e+24]]