题目描述

给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。

示例 1:

输入: numRows = 5

输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

示例 2:

输入: numRows = 1
输出: [[1]]

提示:

1 <= numRows <= 30

方法一：数学

思路及解法

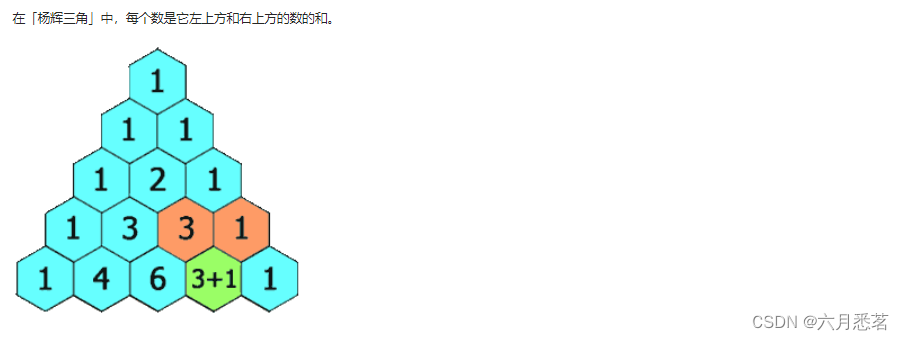
杨辉三角，是二项式系数在三角形中的一种几何排列。它是中国古代数学的杰出研究成果之一，它把二项式系数图形化，把组合数内在的一些代数性质直观地从图形中体现出来，是一种离散型的数与形的结合。

杨辉三角具有以下性质：

代码

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
int** generate(int numRows, int* returnSize, int** returnColumnSizes) {
    // Allocate memory for the 2D array to store Pascal's Triangle
    int** ret = malloc(sizeof(int*) * numRows);
    
    // Set the returnSize to the number of rows
    *returnSize = numRows;
    
    // Allocate memory for an array to store the size of each row in the triangle
    *returnColumnSizes = malloc(sizeof(int) * numRows);
    
    // Loop through each row of the triangle
    for (int i = 0; i < numRows; ++i) {
        // Allocate memory for the current row
        ret[i] = malloc(sizeof(int) * (i + 1));
        
        // Set the size of the current row in the returnColumnSizes array
        (*returnColumnSizes)[i] = i + 1;
        
        // Set the first and last element of the current row to 1
        ret[i][0] = ret[i][i] = 1;
        
        // Populate the rest of the elements in the current row based on the previous row
        for (int j = 1; j < i; ++j) {
            ret[i][j] = ret[i - 1][j] + ret[i - 1][j - 1];
        }
    }
    
    // Return the generated Pascal's Triangle
    return ret;
}

复杂度分析

时间复杂度：O(numRows^2)。

空间复杂度：O(1)。不考虑返回值的空间占用。

作者：力扣官方题解
链接：https://leetcode.cn/problems/pascals-triangle/solutions/510638/yang-hui-san-jiao-by-leetcode-solution-lew9/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。