题目

树可以看成是一个连通且 无环 的 无向 图。

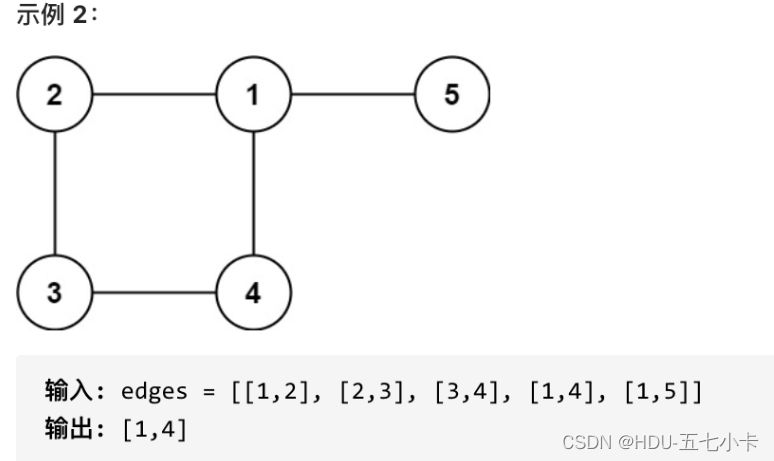
给定往一棵 n 个节点 (节点值 1～n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n
中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [ai, bi]
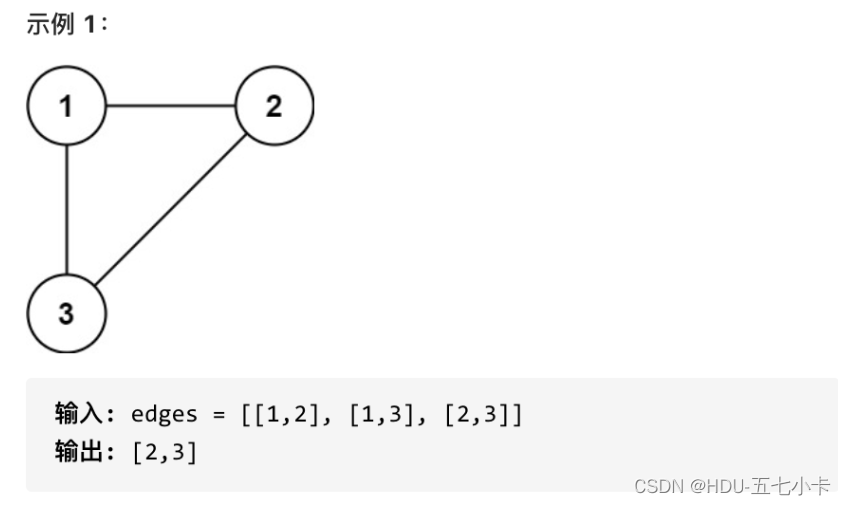
表示图中在 ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的边。
提示:


提示:

n == edges.length
3 <= n <= 1000
edges[i].length == 2
1 <= ai < bi <=edges.length
ai != bi
edges 中无重复元素
给定的图是连通的

思路

本题是并查集基础题目；

并查集主要用于解决一些元素分组的问题。它管理一系列不相交的集合,并支持两种操作:

• 合并(Union):把两个不相交的集合合并为一个集合。
• 查询(Find):查询两个元素是否在同一个集合中。

即并查集主要是解决就是集合问题，看两个节点在不在一个集合，也可以将两个节点添加到一个集合中

并查集模板如下：

int n = 1005;//节点数量3 到 1000
int father[1005];

//并查集初始化
void init(){
	for(int i = 0; i < n; i++){
		father[i] = i;
	}
}
//并查集里寻根的过程
int find(int u){//找节点u的祖先节点
	if(u == father[u]){//如果u的祖先节点就是自己
		return u;
	}
	father[u] = find(father[u]);//否则继续找下去
	return father[u];
}
//将v->u 这条边加入并查集
void join(int u, int v){
	u = find(u);//找到u的祖先
	v = find(v);//找到v的祖先
	if(u == v) return;//如果相同，说明两个节点已经在一个集合中
	father[v] = u;//否则，加入这条边
}
//判断 u 和 v 是否找到同一个根,即是否在同一个集合中
bool same(int u ,  int v){//判断两个节点在不在同一个集合中
	u = find(u);
	v = find(v);
	return u == v;
}

具体只需要修改n和father数组的大小就可以了

并查集有三个功能：

1. 寻找根节点，函数：find(int u)，也就是判断节点 u 的祖先节点是哪个
2. 将两个节点接入到同一个集合，函数：join(int u, int v)，将两个节点 u和 v连在同一个根节点上
3. 判断两个节点是否在同一个集合，函数：same(int u, int v)，就是判断两个节点是不是同一个根节点

在本题中，题意为无向图，返回一条可以删去的边，使得结果图是一个有着N个节点的树，如果有多个答案，则返回二维数组中最后出现的边。

那么就可以从前向后遍历每一条边，边的两个节点如果不在同一个集合，就加入集合（即：同一个根节点）。

如果边的两个节点已经出现在同一个集合里，说明这条边的两个节点已经连在一起了，如果再加入这条边一定就出现环了。

java代码如下：

class Solution {
	private int n;
	private int[] father;
	public 	Solution(){
		n = 1005;
		father = new int[n];
		
		//并查集初始化
		for(int i =  0; i < n; i++){
			father[i] = i;
		}
	}
	
	// 并查集里寻根的过程,找父节点
	public int find(int u){
		if(u == father[u]){
			return u;
		}
		father[u] = find(father[u]);
		return father[u];
	}
	
	//将v->u 这条边加入并查集
	public void join(int u, int v){
		u = find(u);
		v = find(v);
		if(u == v) return;
		fatjer[v] = u;
	}
		
	public boolean same(int u, int v){
		u = find(u);
		v = find(v);
		return u == v;
	}
		
	public int[] findRedundantConnection(int[][] edges){
		for(int i = 0; i < edges.length; i++){
			if(same(edges[i][0],edges[i][1])){//edges[i][0] 表示第i条边的起始节点，edges[i][1]表示第i条边的结束节点,这里的判断就是说这条边的两个节点是否在同一个集合中，如果在的话，那就说明这两个节点之间连接的这条边是冗余连接，会构成环，需要删除
				return edges[i];//如果在同一个集合中，说明这条边是冗余的，加入后会成环，返回这条边
			} else {
				join(edges[i][0],edges[i][1]);//否则加入这条边
			}
		}
		return null;
	}
}

其中，主函数的代码很少，就判断一下边的两个节点在不在同一个集合就可以了