近年来,随着Transformer、MOE架构的提出,使得深度学习模型轻松突破上万亿规模参数,从而导致模型变得越来越大,因此,我们需要一些大模型压缩技术来降低模型部署的成本,并提升模型的推理性能。
模型压缩主要分为如下几类:
- 剪枝(Pruning)
- 知识蒸馏(Knowledge Distillation)
- 量化Quantization)
本系列将针对一些常见大模型量化方案(GPTQ、LLM.int8()、SmoothQuant、AWQ等)进行讲述。
- 大模型量化概述
- 量化感知训练:
- 大模型量化感知训练技术原理:LLM-QAT
- 大模型量化感知微调技术原理:QLoRA
- 训练后量化:
- 大模型量化技术原理:GPTQ、LLM.int8()
- 大模型量化技术原理:SmoothQuant
- 大模型量化技术原理:AWQ、AutoAWQ
- 大模型量化技术原理:SpQR
- 大模型量化技术原理:ZeroQuant系列
- 大模型量化技术原理:总结
而本文主要针对大模型量化技术 SmoothQuant 进行讲述。
另外,我撰写的大模型相关的博客及配套代码均整理放置在Github:llm-action,有需要的朋友自取。
背景
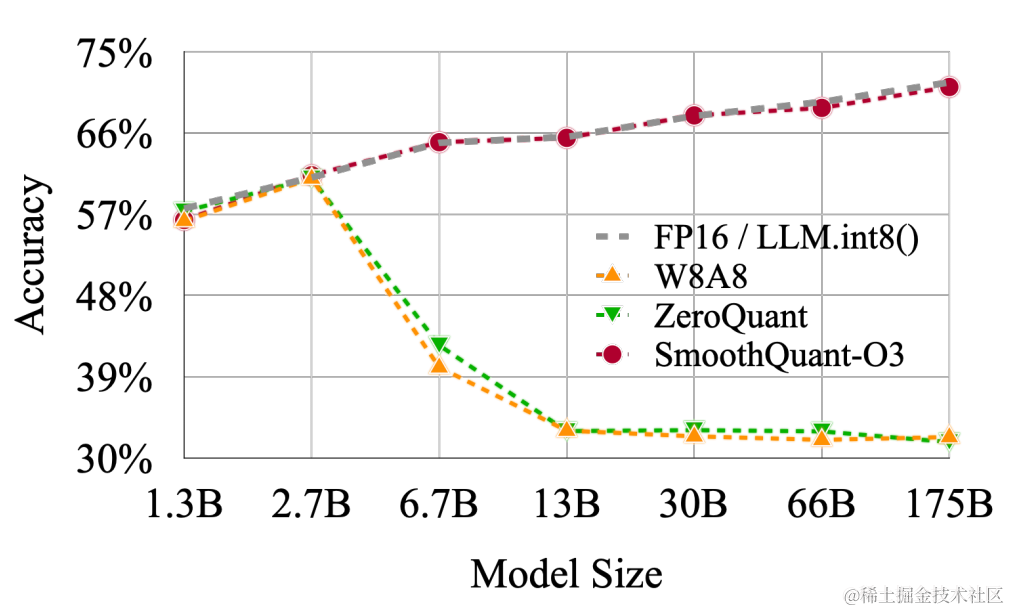
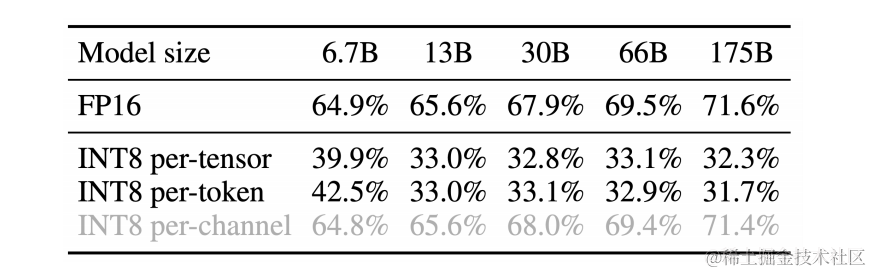
LLM.int8() 发现当 LLMs 的模型参数量超过 6.7B 的时候,激活中会成片的出现大幅的离群点(outliers),朴素且高效的量化方法(W8A8、ZeroQuant等)会导致量化误差增大,精度下降。
但好在新出现的离群特征(Emergent Features)的分布是有规律的。通常,这些离群特征只分布在 Transformer 层的少数几个维度。针对这个问题,LLM.int8() 采用了混合精度分解计算的方式(离群点和其对应的权重使用 FP16 计算,其他量化成 INT8 后计算)。虽然能确保精度损失较小,但由于需要运行时进行异常值检测、scattering 和 gathering,导致它比 FP16 推理慢。
这些激活上的离群点会出现在几乎所有的 token 上但是局限于隐层维度上的固定的 channel 中;给定一个 token,不同 channels 间的方差会很大,但是对于不同的 token,相同 channel 内的方差很小。考虑到激活中的这些离群点通常是其他激活值的 100 倍,这使得激活量化变得困难。
以上是大模型量化困难的原因,总结下来就三点:
- 激活比权重更难量化(之前的工作LLM.int8()表明,使用 INT8 甚至 INT4 量化 LLM 的权重不会降低准确性。)
- 异常值让激活量化更困难(激活异常值比大多数激活值大约 100 倍。 如果我们使用 INT8 量化,大多数值将被清零。)
- 异常值持续存在于固定的通道(channel)中(固定通道存在异常值,并且异常值通道值较大)
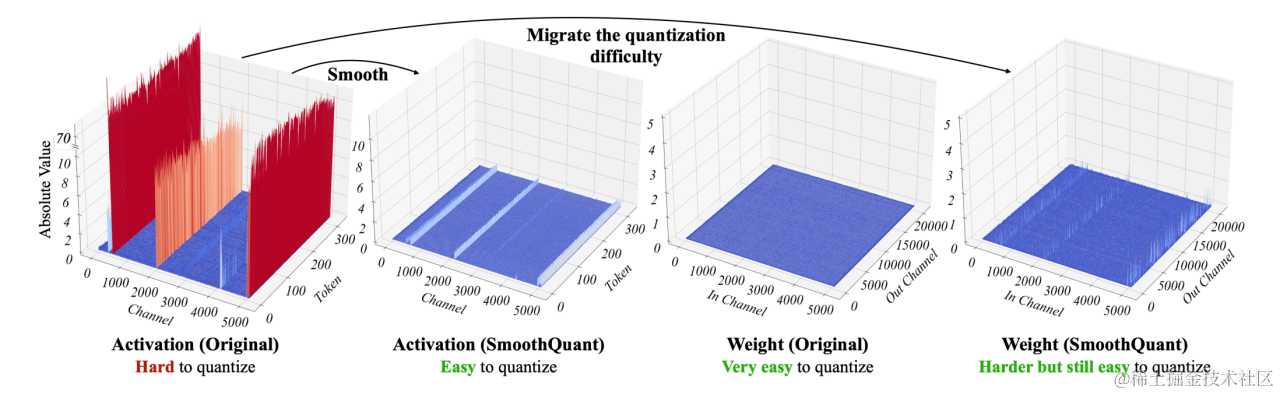
根据量化参数s(数据量化的间隔)和z(数据偏移的偏置)的共享范围,即量化粒度的不同,量化方法可以分为逐层量化(per-tensor)、逐通道(per-token & per-channel 或者 vector-wise quantization )量化和逐组量化(per-group、Group-wise)。
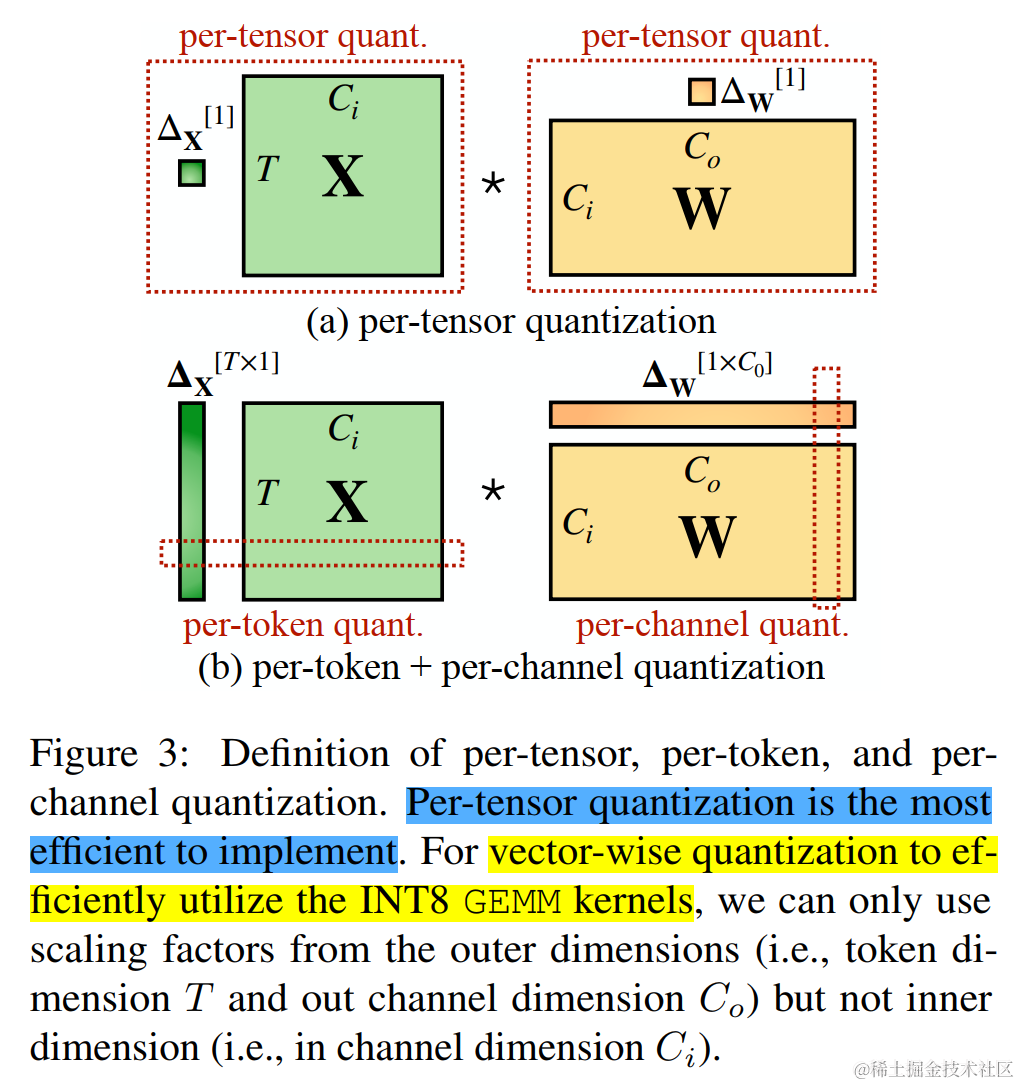
作者对比了 per-channel、per-token、per-tensor 激活量化方案。在这几种不同的激活量化方案中。per-tensor量化是最高效的实现方式。但只有逐通道量化(per-channel)保留了精度,因它与 INT8 GEMM 内核不兼容。即per-channel量化不能很好地映射到硬件加速的GEMM内核(硬件不能高效执行,从而增加了计算时间)。
为了进行 vector-wise quantization 以有效利用 INT8 GEMM 内核,我们只能使用外部维度(即Token维度 T 和 通道外维度 C 0 C_0 C0)的缩放因子,不能使用内部维度(即通道内维度 C i C_i Ci),因此,先前的工作对激活都采用了per-token量化,但并不能降低激活的难度。
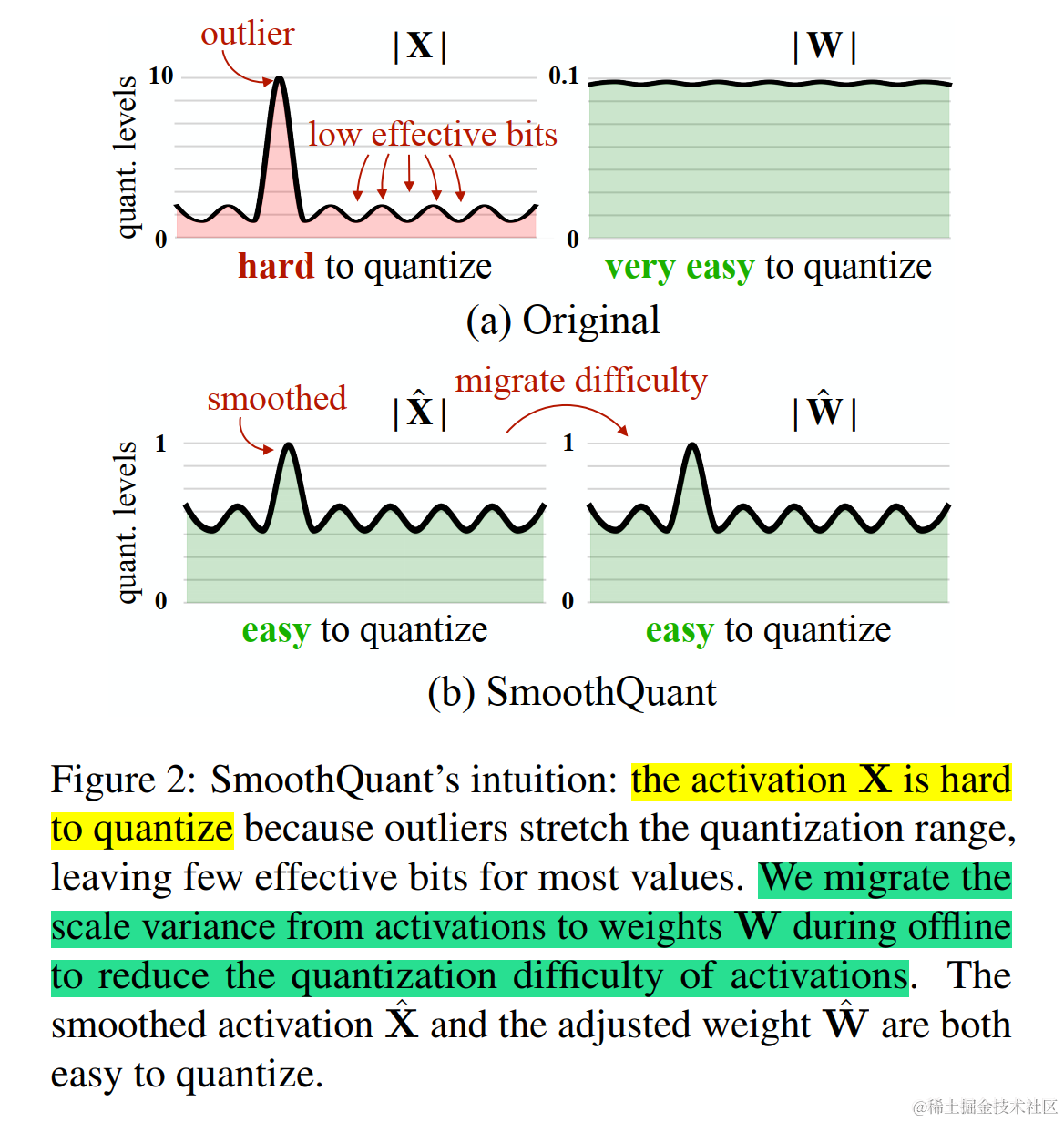
于是 SmoothQuant 提出了一种数学上等价的逐通道缩放变换(per-channel scaling transformation),可显著平滑通道间的幅度,从而使模型易于量化,保持精度的同时,还能够保证推理提升推理速度。
SmoothQuant 技术原理
SmoothQuant (论文:SmoothQuant: Accurate and Efficient Post-Training Quantization for Large Language Models)是一种同时确保准确率且推理高效的训练后量化 (PTQ) 方法,可实现 8 比特权重、8 比特激活 (W8A8) 量化。由于权重很容易量化,而激活则较难量化,因此,SmoothQuant 引入平滑因子s来平滑激活异常值,通过数学上等效的变换将量化难度从激活转移到权重上。
常规的矩阵乘如下:
Y = X W Y=XW Y=XW
SmoothQuant 对激活进行 smooth,按通道除以 smoothing factor。为了保持线性层数学上的等价性,以相反的方式对权重进行对应调整。SmoothQuant 的矩阵乘如下:
Y = ( X d i a g ( s ) − 1 ) ⋅ ( d i a g ( s ) − 1 W ) = X ^ W ^ Y=(Xdiag(s)^{-1}) \cdot (diag(s)^{-1}W)=\hat{X} \hat{W} Y=(Xdiag(s)−1)⋅(diag(s)−1W)=X^W^
$X \in R ^{T \times C_i} $ 在 channel 维度(列)上每个元素除以 s i s_i si ,$ W \in R ^{ C_i \times C_0} 则在每行上每个元素乘以 则在每行上每个元素乘以 则在每行上每个元素乘以 s_i$ 。这样 Y 在数学上是完全相等的,平滑因子s的计算公式下面会讲述。
将量化难度从激活迁移到权重
为了减小量化误差,可以为所有 channels 增加有效量化 bits。当所有 channels 都拥有相同的最大值时,有效量化 bits 将会最大。
一种做法是让 s j = m a x ( ∣ X j ∣ ) , j = 1 , 2 , . . . , C j s_j=max(|X_j|),j=1,2,...,C_j sj=max(∣Xj∣),j=1,2,...,Cj , C j C_j Cj 代表第 j 个 input channel。各 channel 通过除以 s j s_j sj 后,激活 channels 都将有相同的最大值,这时激活比较容易量化。但是这种做法会把激活的量化难度全部转向权重,导致一个比较大的精度损失。
另一种做法是让 s j = 1 / m a x ( ∣ W j ∣ ) s_j=1/max(|W_j|) sj=1/max(∣Wj∣),这样权重 channels 都将有相同的最大值,权重易量化,但激活量化误差会很大。
因此,我们需要在 weight 和 activation 中平衡量化难度,让彼此均容易被量化。本文作者通过加入一个超参 $ \alpha (迁移强度),来控制从激活值迁移多少难度到权重值。一个合适的迁移强度值能够让权重和激活都易于量化。 (迁移强度),来控制从激活值迁移多少难度到权重值。一个合适的迁移强度值能够让权重和激活都易于量化。 (迁移强度),来控制从激活值迁移多少难度到权重值。一个合适的迁移强度值能够让权重和激活都易于量化。 \alpha 太大,权重难以量化, 太大,权重难以量化, 太大,权重难以量化, \alpha $ 太小激活难以量化。
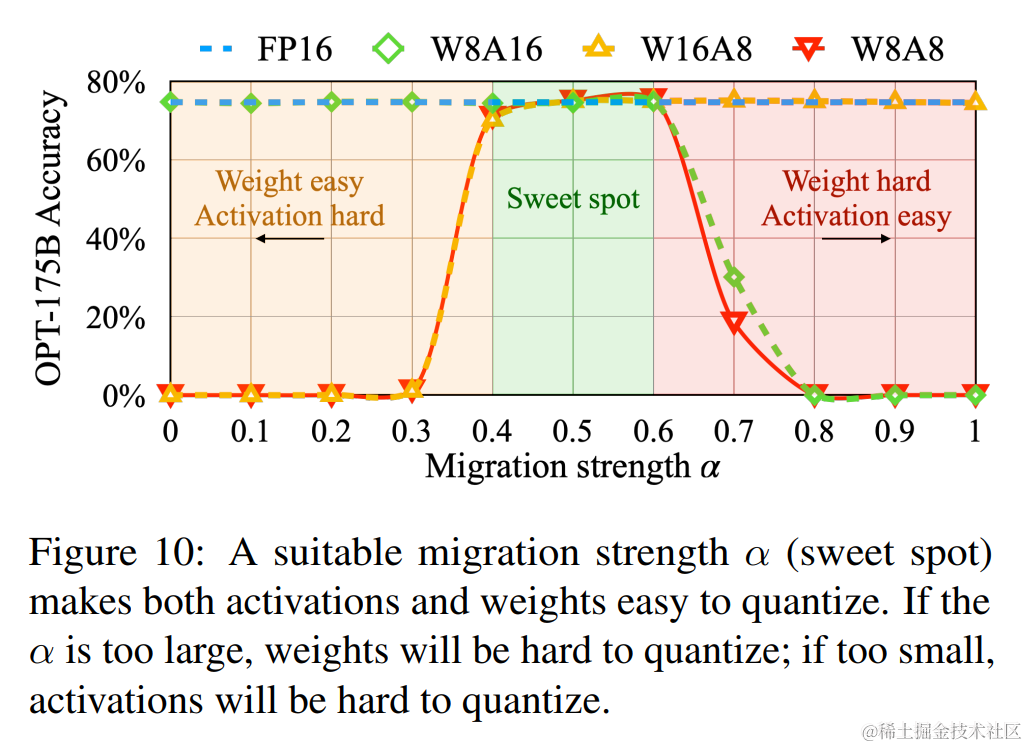
通过实验发现,针对 OPT 和 BLOOM 模型, $ \alpha = 0.5 是一个很好的平衡点;针对 G L M − 130 B ,该模型有 30 =0.5 是一个很好的平衡点;针对 GLM-130B,该模型有 30%的异常值,激活值量化难度更大,可以选择 =0.5 是一个很好的平衡点;针对GLM−130B,该模型有30 \alpha $=0.75 。
下图展示了当 α 为 0.5 时 SmoothQuant 的主要思想。

平滑因子 s 是在校准样本上获得的,整个转换是离线执行的。在运行时,激活是平滑的,无需缩放,具体步骤如下:
- 校准阶段(离线)
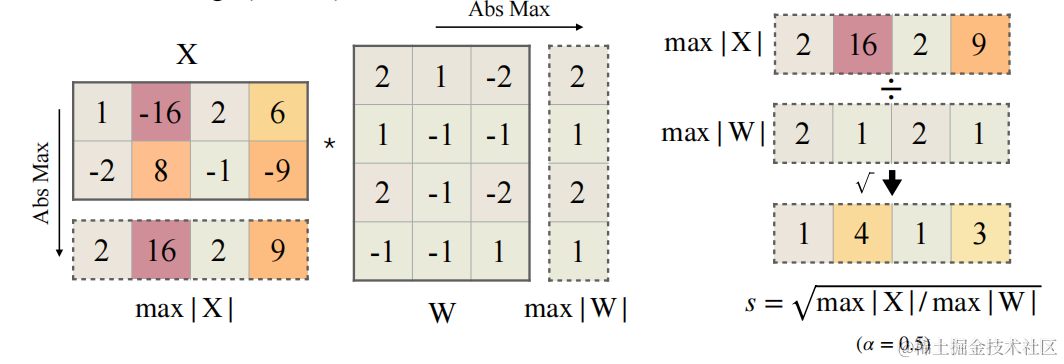
平滑因子s的计算公式如下:
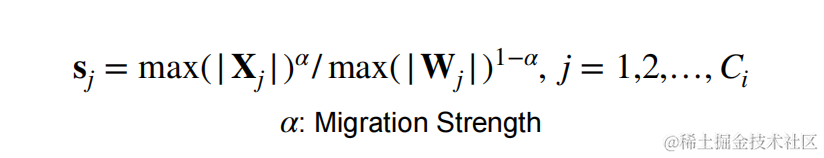
- $ \alpha $ 表示迁移强度,为一个超参数,控制将多少激活值的量化难度迁移到权重量化。
- C C C 表示激活的输入通道数。
- 平滑阶段(离线)
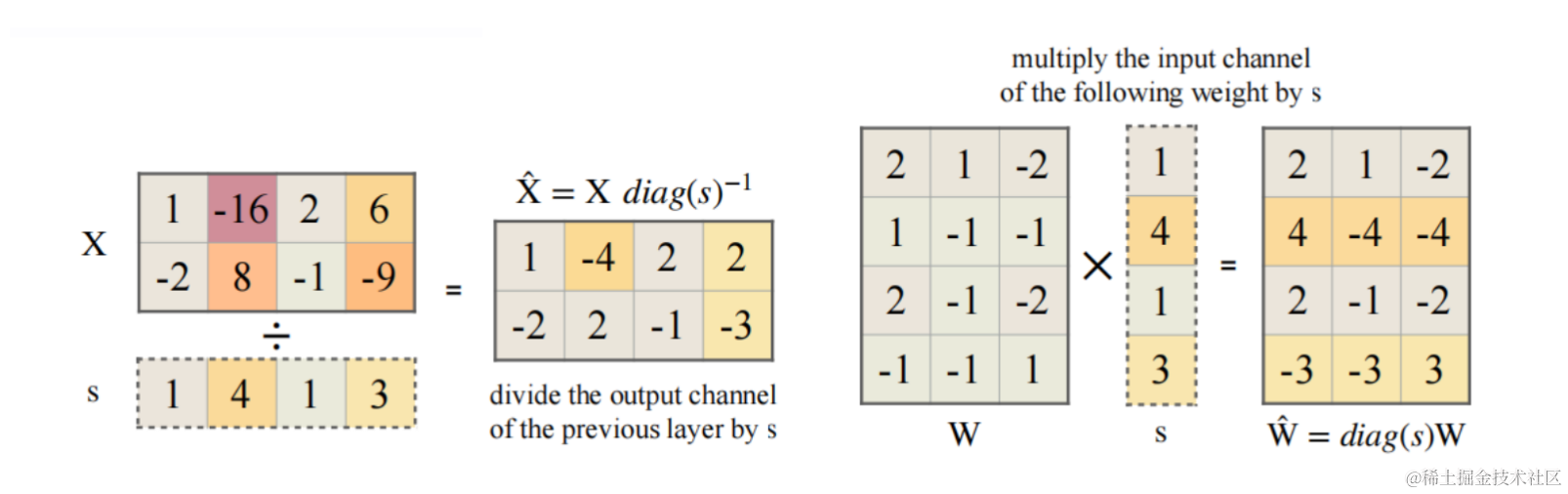
X ^ , W ^ \hat{X}, \hat{W} X^,W^ 的计算公式如下:
- $\hat{W}=diag(s) W $
- X ^ = X d i a g ( s ) − 1 \hat{X}=X diag(s)^{-1} X^=Xdiag(s)−1
- 推理阶段(在线,部署模型)
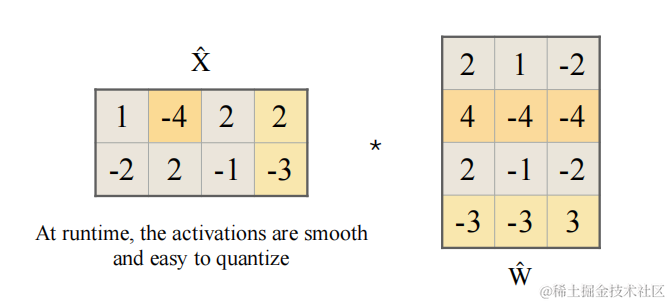
平滑之后的激活的计算公式如下:
Y = X ^ W ^ Y = \hat{X} \hat{W} Y=X^W^
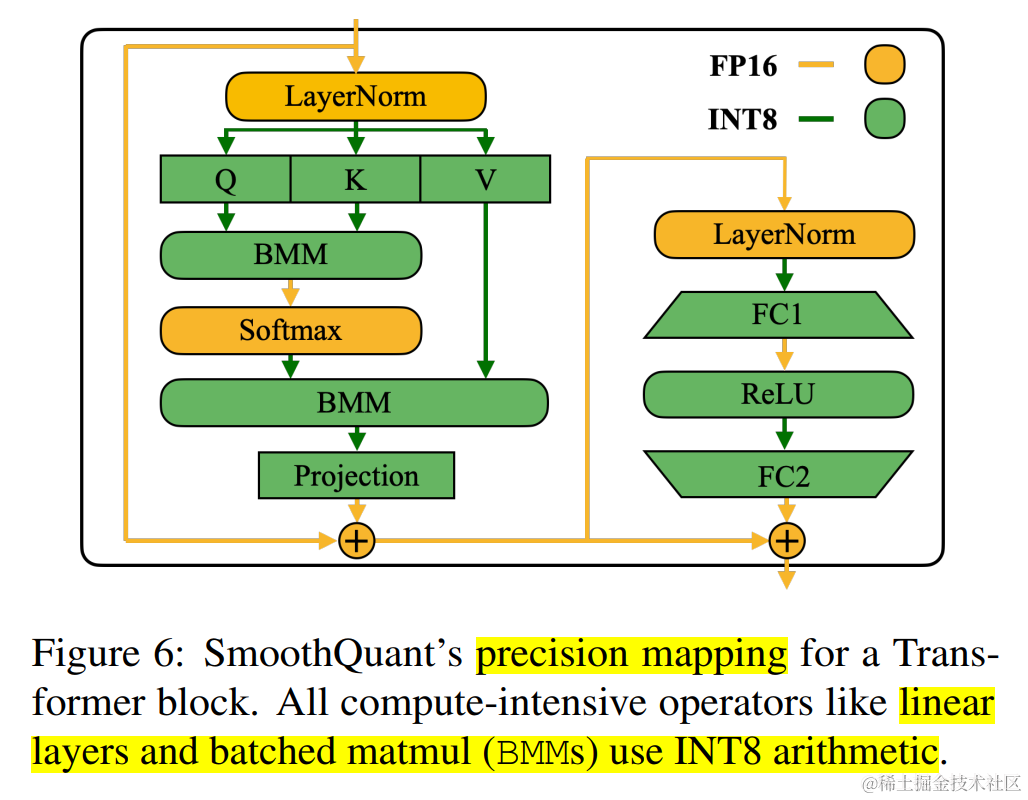
将 SmoothQuant 应用于 Transformer 块
在Transformer 块中,将所有计算密集型算子(如:线性层、batched matmul (BMMs) )使用 INT8 运算,同时将其他轻量级算子(如:LayerNorm/Softmax)使用 FP16 运算 ,这样可以均衡精度和推理效率。
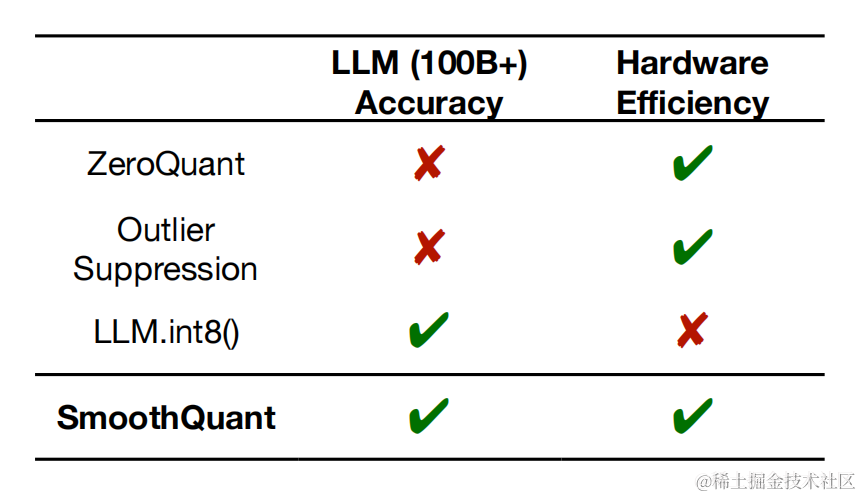
SmoothQuant 推理性能及精度
SmoothQuant可以无损地量化所有超过100B参数的开源LLM。
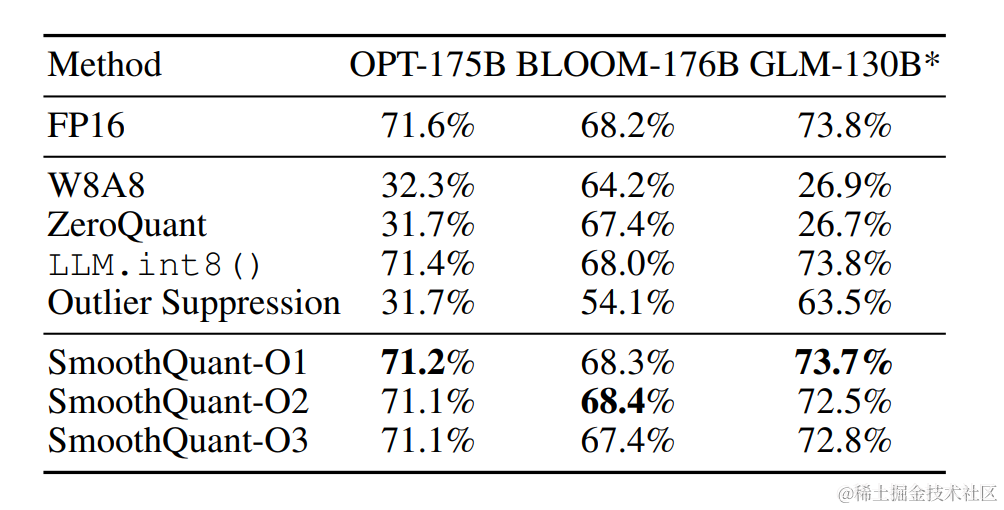
根据量化方式不同,作者提出三种策略 O1、O2、O3,其计算延迟依次降低。SmoothQuant的O1和O2级成功地保持了浮点精度,而O3级(per-tensor static)使平均精度下降了0.8%,可能是因为静态收集的统计数据与真实评估样本的激活统计数据之间的差异。

OPT-175B 使用 SmoothQuant 进行 int8 量化之后保持了与FP16相当的精度。
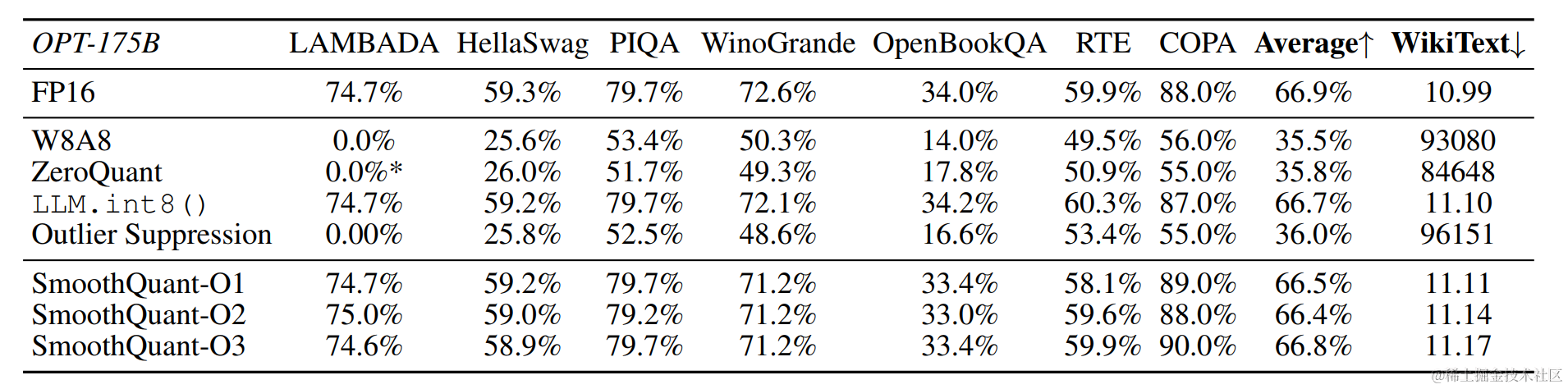
对于不同的LLM,SmoothQuant 相比其他量化方法(如:LLM.int8()、ZeroQuant等)具有更高的精度。
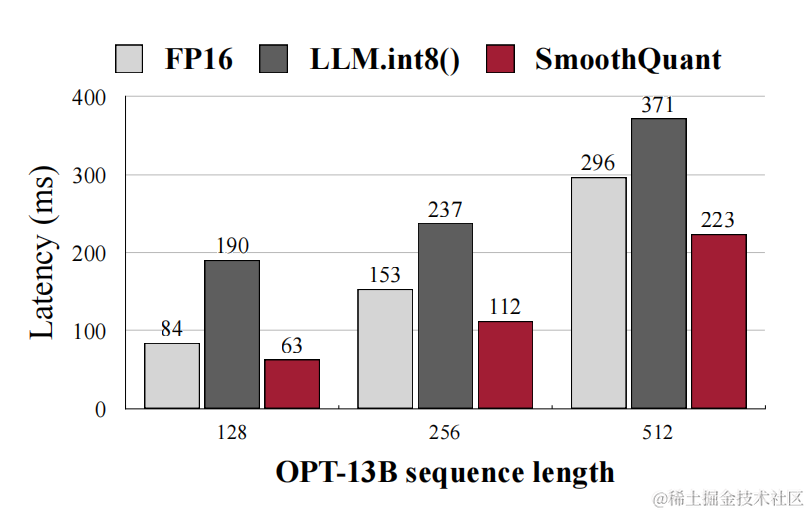
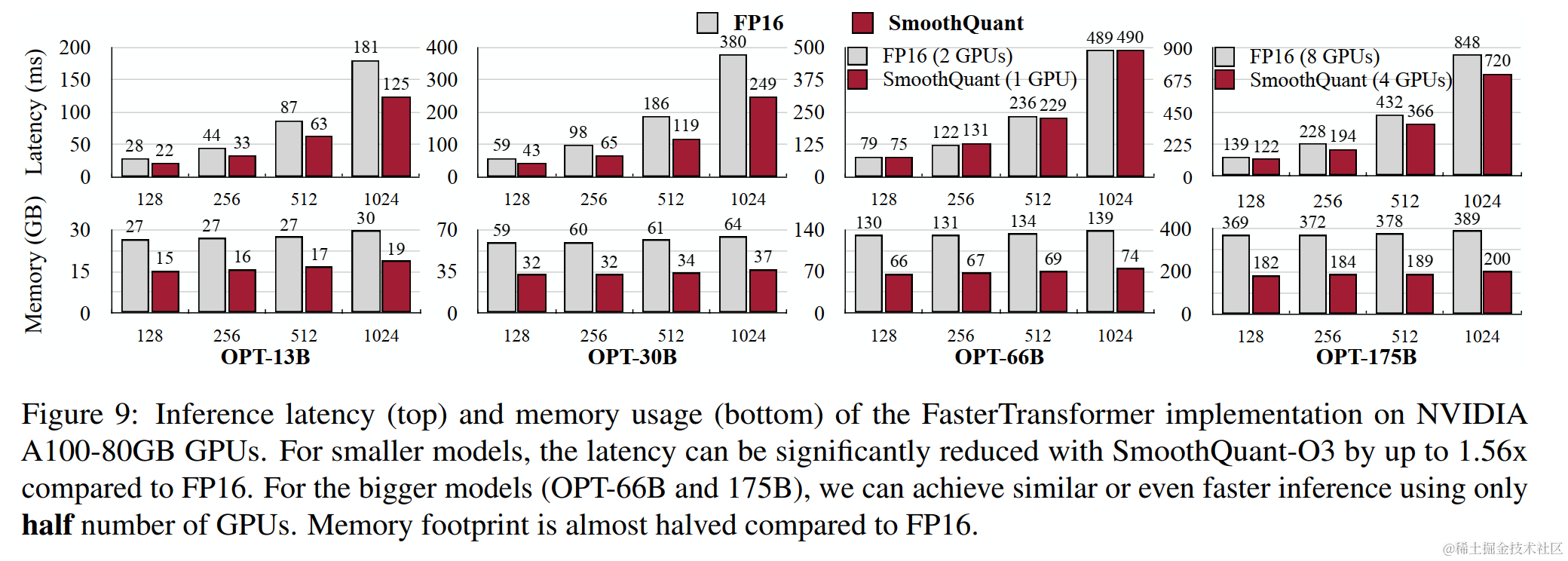
作者将SmoothQuant集成到PyTorch和FasterTransformer中,与 FP16 相比,获得高达1.56倍的推理加速,并将内存占用减半,并且模型越大,加速效果越明显。
SmoothQuant 应用
官方示例:
- generate_act_scales.py:生成激活 scales
- export_int8_model.py:平滑、量化以及导出INT8模型
- smoothquant_opt_demo.ipynb:SmoothQuant 伪量化示例
- smoothquant_opt_real_int8_demo.ipynb:SmoothQuant 真正的量化示例
使用 FP16 模拟 8 比特动态 per- tensor 权重和激活量化,即伪量化。
import torch
from transformers.models.opt.modeling_opt import OPTAttention, OPTDecoderLayer, OPTForCausalLM
from smoothquant.smooth import smooth_lm
from smoothquant.fake_quant import W8A8Linear
# 模型量化
def quantize_model(model, weight_quant='per_tensor', act_quant='per_tensor', quantize_bmm_input=True):
for name, m in model.model.named_modules():
if isinstance(m, OPTDecoderLayer):
m.fc1 = W8A8Linear.from_float(m.fc1, weight_quant=weight_quant, act_quant=act_quant)
m.fc2 = W8A8Linear.from_float(m.fc2, weight_quant=weight_quant, act_quant=act_quant)
elif isinstance(m, OPTAttention):
# Her we simulate quantizing BMM inputs by quantizing the output of q_proj, k_proj, v_proj
m.q_proj = W8A8Linear.from_float(
m.q_proj, weight_quant=weight_quant, act_quant=act_quant, quantize_output=quantize_bmm_input)
m.k_proj = W8A8Linear.from_float(
m.k_proj, weight_quant=weight_quant, act_quant=act_quant, quantize_output=quantize_bmm_input)
m.v_proj = W8A8Linear.from_float(
m.v_proj, weight_quant=weight_quant, act_quant=act_quant, quantize_output=quantize_bmm_input)
m.out_proj = W8A8Linear.from_float(m.out_proj, weight_quant=weight_quant, act_quant=act_quant)
return model
# 原生 W8A8 模型量化
model_fp16 = OPTForCausalLM.from_pretrained('facebook/opt-13b', torch_dtype=torch.float16, device_map='auto')
model_w8a8 = quantize_model(model_fp16)
print(model_w8a8)
# SmoothQuant W8A8 模型量化(伪量化)
model = OPTForCausalLM.from_pretrained('facebook/opt-13b', torch_dtype=torch.float16, device_map='auto')
# 激活scales
act_scales = torch.load('../act_scales/opt-13b.pt')
smooth_lm(model, act_scales, 0.5)
model_smoothquant_w8a8 = quantize_model(model)
print(model_smoothquant_w8a8)
作者使用 CUTLASS INT8 GEMM 内核为 PyTorch 实现 SmoothQuant 真正的 INT8 推理,这些内核被包装为 torch-int 中的 PyTorch 模块。加载SmoothQuant量化后的模型示例如下:
from smoothquant.opt import Int8OPTForCausalLM
def print_model_size(model):
# https://discuss.pytorch.org/t/finding-model-size/130275
param_size = 0
for param in model.parameters():
param_size += param.nelement() * param.element_size()
buffer_size = 0
for buffer in model.buffers():
buffer_size += buffer.nelement() * buffer.element_size()
size_all_mb = (param_size + buffer_size) / 1024**2
print('Model size: {:.3f}MB'.format(size_all_mb))
model_smoothquant = Int8OPTForCausalLM.from_pretrained(
'mit-han-lab/opt-30b-smoothquant', torch_dtype=torch.float16, device_map='auto')
print_model_size(model_smoothquant)
SmoothQuant 生态
目前,SmoothQuant 已经集成到了英伟达的 TensorRT-LLM 推理加速工具以及英特尔的 Neural-Compressor 模型压缩工具包中。
总结
本文简要介绍了诞生的SmoothQuant背景和技术原理,作者提到激活值比权重更难量化,因为权重数据分布一般比较均匀,而激活异常值多且大让激活值量化变得更艰难,但是异常值只存在少数通道(Channel)内(单一 token 方差很大(异常值会存在于每一个 token 中),单一 channel 方差会小很多)。
因此,SmoothQuant 诞生。SmoothQuant 通过平滑激活层和权重后,再使用per-tensor或per-token量化,实现W8A8。根据量化方式不同,作者提出三种策略 O1、O2、O3,计算延迟依次降低。与其他量化方法相比,该方法可以保持较高的精度,同时,具有更低的延迟。
码字不易,如果觉得我的文章能够能够给您带来帮助,期待您的点赞收藏加关注~~
参考文档
- https://github.com/mit-han-lab/smoothquant
- https://arxiv.org/pdf/2211.10438.pdf
- https://github.com/mit-han-lab/smoothquant/blob/main/assets/SmoothQuant.pdf
- https://blog.csdn.net/LoveJSH/article/details/132114469
- 大语言模型的模型量化(INT8/INT4):https://zhuanlan.zhihu.com/p/627436535
- SmoothQuant Real-INT8 Inference for PyTorch:https://github.com/mit-han-lab/smoothquant/blob/main/examples/smoothquant_opt_real_int8_demo.ipynb
- SmoothQuant on OPT-13B:https://github.com/mit-han-lab/smoothquant/blob/main/examples/smoothquant_opt_demo.ipynb