以下内容有任何不理解可以翻看我之前的博客哦:吴恩达deeplearning.ai专栏
文章目录
- 一个小型神经网络的例子
- 利用计算图逐步计算价值函数J
- 利用计算图求出价值函数的导数
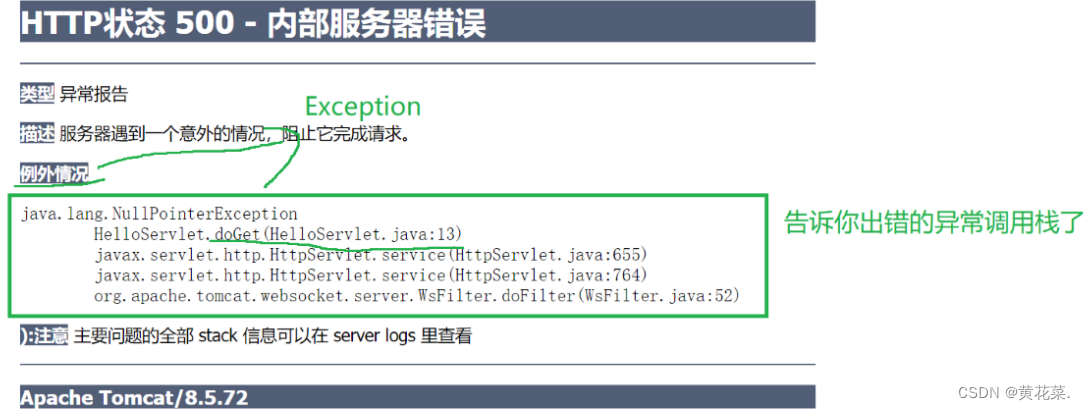
计算图是深度学习中的一个关键概念,它也是Tensorflow等编程框架自动计算神经网络导数的方式。让我们举个例子。
一个小型神经网络的例子

这是一个很小型的神经网络,其中,激活值a满足:
a
=
w
x
+
b
a=wx+b
a=wx+b
之后采用线性激活函数:
a
=
g
(
z
)
=
z
a=g(z)=z
a=g(z)=z
其价值函数为:
J
(
w
,
b
)
=
1
2
(
a
−
y
)
2
J(w,b)=\frac{1}{2}(a-y)^2
J(w,b)=21(a−y)2
对于这种小网络,我们只有一个训练样例:
x
=
−
2
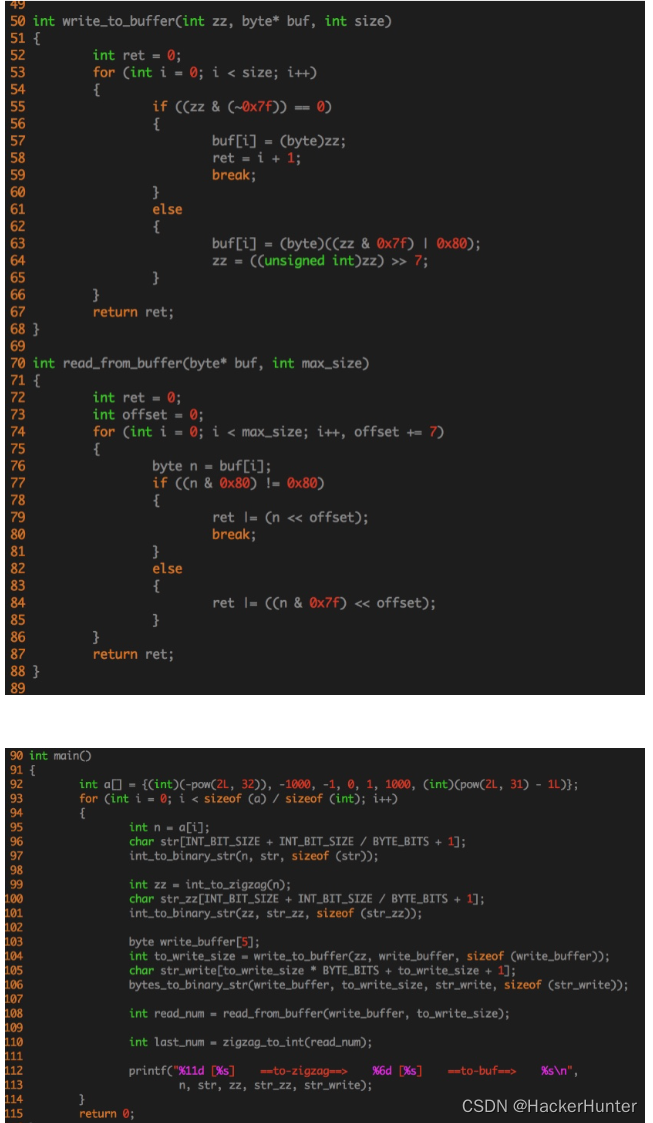
,
y
=
2
x=-2,y=2
x=−2,y=2
该网络的参数为:
w
=
2
,
b
=
8
w=2,b=8
w=2,b=8
我们想要展示的是如何使用计算图来逐步计算价值函数J。
利用计算图逐步计算价值函数J
以下是这个例子的计算图,其实很简单:

这张图从左到右逐步展示了价值函数的计算过程,其中矩形之中描述的是计算步骤,而线段上面所写的是前一步计算出来的值。所以从左到右,依次计算量w*x的值,然后计算出了a的值,再计算出a-y的值,最后求得价值函数,为2。
计算图向我们展现了神经网络向前传播的步骤(图中还更进一步求了价值函数)。现在的问题是,如何利用计算图找到J关于w和b的导数
∂
J
∂
w
\frac{\partial J}{\partial w}
∂w∂J
∂
J
∂
b
\frac{\partial J}{\partial b}
∂b∂J。
利用计算图求出价值函数的导数
事实证明,神经网络的前向传播是从左到右计算,而计算导数是从右向左的计算。

反向传播的第一步是询问d的值,它是价值函数的输入,d改变,J就跟着改变。例如,如果d改变了一内内,比如0.001,那么j将如何变化嘞。结果是在这种情况下,如果d从2变为了2.01,j则从2变味了2.02,那么可以得出结论就是J这里的导数为2,数学公式就是:
∂
J
∂
d
=
2
\frac{\partial J}{\partial d}=2
∂d∂J=2,这样就求出最右边的导数了。
下一步当然是继续向左进行,求一下
∂
J
∂
a
\frac{\partial J}{\partial a}
∂a∂J等于多少。利用与上面同样的方法,可以求出
∂
d
∂
a
=
1
\frac{\partial d}{\partial a}=1
∂a∂d=1,再结合上
∂
J
∂
d
=
2
\frac{\partial J}{\partial d}=2
∂d∂J=2,那么联立就可以得出
∂
J
∂
a
=
2
\frac{\partial J}{\partial a}=2
∂a∂J=2。用数学化的方式来说,以上步骤其实是依靠链式法则进行微积分,高等数学应该学过。其实就是
∂
J
∂
a
=
∂
d
∂
a
×
∂
J
∂
d
\frac{\partial J}{\partial a}=\frac{\partial d}{\partial a}\times \frac{\partial J}{\partial d}
∂a∂J=∂a∂d×∂d∂J。
接下来就是一步步从右到左,最终可以得出:
∂
J
∂
w
=
−
4
\frac{\partial J}{\partial w}=-4
∂w∂J=−4
事实证明,反向传播是计算导数的一个不错的方法,避免了你直接计算导数时过于复杂的复合求导。如果一个图具有n个节点(就是图中的矩形)和p个参数(我们这个例子中有两个参数),我们可以在n+p步中求出J对于所有参数的导数,而非n*p,这就表明即使在大型神经网络中你仍然可以进行求导运算。
为了给读者你造成不必要的麻烦,博主的所有视频都没开仅粉丝可见,如果想要阅读我的其他博客,可以点个小小的关注哦。