阅读facebook开源的 RPC(Remote Procedure Call) 框架thrift源代码的时候,本来是在阅读框架,却不小心被 zigzag 这个钻石般闪耀的代码吸引。后来去百度搜索zigzag,却得到满屏图像相关的一个算法(看来起名字得有特点才行)。既然相关资料很少,而算法又这么有趣,老王就想要不写一篇这个算法的文章,分享给大家。
这个算法的java代码放在thrift的org.apache.thrift.protocol.TCompactProtocol类里,数据传输的时候用做数字的压缩,以减少数据的传输量。
为了写好这篇文章,同时方便大家阅读,老王把这个算法从thrift框架中摘离出来,清理了与算法无关的东西,然后用C语言重新实现了一遍,在文章末尾会完整的贴出来,大家可以围观。
好了,开始正题,跟老王一起来吧~
在聊这个算法之前,我们得先补补课,聊聊进制、补码相关的东东。
1、进制
这个内容是作为码工挣钱最基础的知识之一。所谓进制,全称是进位制,就是当某一个位上的信息满了,需要往前进位。比如,某一位上的信息只能容纳十个,超过十个就往前进一位,则是逢十进一的十进制;如果逢二进一,则是二进制;等等。进制之间是可以转换的,比如十进制的10 等于 二进制的1010, 也等于十六进制的A,通常写作:(10)10=(1010)2=(A)16 。
我之前看一本书就讲现在为什么大家通用的是十进制。一个比较有趣的答案说,因为人类只有10个手指头,数数的时候,挨个儿数过去刚好十个数,所以十进制自然而然成为默认的进制。如果人类是12个手指头,说不定就是十二进制了。
后来计算机的出现,一个数据的有无是最天然的信息承载单元,所以由0-1组成的二进制很天然的成为计算机的进制方式。在此基础上,为方便信息的传递,又采用了八进制、十六进制等进制。
好了,因为大家对进制这个东东其实也是比较了解,我就不多扯了,就先说到这儿。
2、补码
我们对一个十进制的正整数可以采用相关算法,得到他对应的二进制编码,比如:(10)10=(1010)2 。不过,如果我们要表示负整数,怎么办呢?在计算机的世界里,我们就定义了原码、反码和补码这几个东东。
为了描述简单,我们都假设我们的数字用一个字节(1Byte = 8bits)来表示。
A、原码
我们用第一个位表示符号(0为非负数,1为负数),剩下的位表示值。比如:
[+8]=[00001000]原
[−8]=[10001000]原
B、反码
我们用第一位表示符号(0为非负数,1为负数),剩下的位,非负数保持不变,负数按位求反。比如:
[+8]=[00001000]原=[00001000]反
[−8]=[10001000]原=[11110111]反
如果我们用原码或者补码来表示整数的二进制,有什么问题么?表面上看,似乎挺好的。不过仔细思考就会发现两个问题:
第一、0居然用两个编码(+0和-0)来表示了:
原码:[00000000]原=[10000000]原
反码:[00000000]反=[11111111]反
第二、计算机要理解符号位的存在,否则符号位参与运算,就会出现诡异的现象:
原码:
1+(−1)=[00000001]原+[10000001]原=[10000010]原=−2
明显是不对的!
反码:
1+(−1)=[00000001]反+[11111110]反=[11111111]反=−0
表现的好诡异!
为了解决这些问题,我们在计算机体系中引入了补码。
C、补码
我们用第一位表示符号(0为非负数,1为负数),剩下的位非负数保持不变,负数按位求反末位加一。
[+8]=[00001000]原=[00001000]补
[−8]=[10001000]原=[11111000]补
那我们再看看,把符号放进去做运算会有什么样的效果呢?
1+(−1)=[00000001]补+[11111111]补=[00000000]补=0
很明显,通过这样的方式,计算机进行运算的时候,就不用关心符号这个问题,而只需要按照统一的逢二进一的原则进行运算就可以了。
好了,脑补了进制和补码以后,我们就可以进入正题了。
3、zigzag
在绝大多数情况下,我们使用到的整数,往往是比较小的。比如,我们会记录一个用户的id、一本书的id、一个回复的数量等等。在绝大多数系统里面,他们都是一个小整数,就像1234、1024、100等。
而我们在系统之间进行通讯的时候,往往又需要以整型(int)或长整型(long)为基本的传输类型,他们在大多数系统中,以4Bytes和8Bytes来表示。这样,为了传输一个整型(int)1,我们需要传输00000000_00000000_00000000_00000001 32个bits,除了一位是有价值的1,其他全是基本无价值的0(此处发出一个声音:浪!费!啊!)。
那怎么办呢?牛逼的工程师想出了一个小而有趣的算法:zigzag!
这个算法具体的思想是怎么样的呢?
对于正整数来讲,如果在传输的时候,我们把多余的0去掉(或者是尽可能去掉无意义的0),传输有意义的1开始的数据,那我们是不是就可以做到数据的压缩了呢?那怎么样压缩无意义的0呢?
答案也很简单,比如:00000000_00000000_00000000_00000001 这个数字,我们如果能只发送一位1或者一个字节00000001,是不是就将压缩很多额外的数据呢?
当然,如果这个世界只有正整数,我们就会很方便的做到这一点。可惜,他居然还有负数!!!负数长什么样呢?(−1)10=(11111111_11111111_11111111_11111111)补 ,前面全是1,你说怎么弄?!
zigzag给出了一个很巧的方法:我们之前讲补码讲过,补码的第一位是符号位,他阻碍了我们对于前导0的压缩,那么,我们就把这个符号位放到补码的最后,其他位整体前移一位:
(−1)10=(11111111_11111111_11111111_11111111)补=(11111111_11111111_11111111_11111111)符号后移
但是即使这样,也是很难压缩的,因为数字绝对值越小,他所含的前导1越多。于是,这个算法就把负数的所有数据位按位求反,符号位保持不变,得到了这样的整数:
(−1)10=(11111111_11111111_11111111_11111111)补=(11111111_11111111_11111111_11111111)符号后移=(00000000_00000000_00000000_00000001)zigzag
而对于非负整数,同样的将符号位移动到最后,其他位往前挪一位,数据保持不变。
(1)10=(00000000_00000000_00000000_00000001)补=(00000000_00000000_00000000_00000010)符号后移=(00000000_00000000_00000000_00000010)zigzag
唉,这样一弄,正数、0、负数都有同样的表示方法了。我们就可以对小整数进行压缩了,对吧~
这两种case,合并到一起,就可以写成如下的算法:
整型值转换成zigzag值:
int int_to_zigzag(int n)
{
return (n << 1) ^ (n >> 31);
}
n << 1 : 将整个值左移一位,不管正数、0、负数他们的最后一位就变成了0;
(1)10=(00000000_00000000_00000000_00000001)补左移一位=>(00000000_00000000_00000000_00000010)补
(−1)10=(11111111_11111111_11111111_11111111)补左移一位=>(11111111_11111111_11111111_11111110)补
n >> 31 : 将符号位放到最后一位。如果是非负数,则为全0;如果是负数,就是全1。
(1)10=(00000000_00000000_00000000_00000001)补右移31位=>(00000000_00000000_00000000_00000000)补
(−1)10=(11111111_11111111_11111111_11111111)补右移31位=>(11111111_11111111_11111111_11111111)补
最后这一步很巧妙,将两者进行按位异或操作:
(1)10=>(00000000_00000000_00000000_00000010)补
^ (00000000_00000000_00000000_00000000)补=(00000000_00000000_00000000_00000010)补
可以看到最终结果,数据位保持不变,而符号位也保持不变,只是符号位移动到了最后一位
(−1)10=>(11111111_11111111_11111111_11111110)补
^ (11111111_11111111_11111111_11111111)补=(00000000_00000000_00000000_00000001)补
可以看到,数据位全部反转了,而符号位保持不变,且移动到了最后一位。
就是这一行代码,就将这个相对复杂的操作做完了,真是写的巧妙。
zigzag值还原为整型值:
int zigzag_to_int(int n)
{
return (((unsigned int)n) >> 1) ^ -(n & 1);
}
类似的,我们还原的代码就反过来写就可以了。不过这里要注意一点,就是右移的时候,需要用不带符号的移动,否则如果第一位数据位是1的话,就会补1。所以,代码里用了无符号的右移操作:(((unsigned int)n) >> 1)。在java代码里,对应的移位操作:n >>> 1。
好了,有了算法对数字进行转换以后,我们就得到了有前导0的另外一个整数了。不过他还是一个 4字节 的整数,我们接下来就要考虑怎么样将他们表示成尽可能少的字节数,并且还能还原。
比如:我们将1转换成(00000000_00000000_00000000_00000010)zigzag这个以后,我们最好只需要发送2bits(10),或者发送8bits(00000010),把前面的0全部省掉。因为数据传输是以字节为单位,所以,我们最好保持8bits这样的单位。所以我们有几种做法:
A、我们可以额外增加一个字节,用来表示接下来有效的字节长度,比如:00000001_00000010,前8位表示接下来有1个字节需要传输,第二8位表示真正的数据。这种方式虽然能达到我们想要的效果,但是莫名的增加一个字节的额外浪费。有没有不浪费的办法呢?
B、字节自表示方法。zigzag引入了一个方法,就是用字节自己表示自己。具体怎么做呢?我们来看看代码:
int write_to_buffer(int zz, byte* buf, int size)
{
int ret = 0;
for (int i = 0; i < size; i++)
{
if ((zz & (~0x7f)) == 0)
{
buf[i] = (byte)zz;
ret = i + 1;
break;
}
else
{
buf[i] = (byte)((zz & 0x7f) | 0x80);
zz = ((unsigned int)zz) >> 7;
}
}
return ret;
}
大家先看看代码里那个(~0x7f),他究竟是个什么数呢?
( 0x7f)16=(11111111_11111111_11111111_10000000)补
他就是从倒数第八位开始,高位全为1的数。他的作用,就是看除开最后七位后,还有没有信息。
我们把zigzag值传递给这个函数,这个函数就将这个值从低位到高位切分成每7bits一组,如果高位还有有效信息,则给这7bits补上1个bit的1(0x80)。如此反复 直到全是前导0,便结束算法。
举个例来讲:
(−1000)10=(11111111_11111111_11111100_00011000)补=(00000000_00000000_00000111_11001111)zigzag
我们先按照七位一组的方式将上面的数字划开:
(0000−0000000−0000000−0001111−1001111)zigzag
A、他跟(~0x7f)做与操作的结果,高位还有信息,所以,我们把低7位取出来,并在倒数第八位上补一个1(0x80):11001111
B、将这个数右移七位:(0000−0000000−0000000−0000000−0001111)zigzag
C、再取出最后的七位,跟(~0x7f)做与操作,发现高位已经没有信息了(全是0),那么我们就将最后8位完整的取出来:00001111,并且跳出循环,终止算法;
D、最终,我们就得到了两个字节的数据[11001111, 00001111]
通过上面几步,我们就将一个4字节的zigzag变换后的数字变成了一个2字节的数据。如果我们是网络传输的话,就直接发送这2个字节给对方进程。对方进程收到数据后,就可以进行数据的组装还原了。具体的还原操作如下:
int read_from_buffer(byte* buf, int max_size)
{
int ret = 0;
int offset = 0;
for (int i = 0; i < max_size; i++, offset += 7)
{
byte n = buf[i];
if ((n & 0x80) != 0x80)
{
ret |= (n << offset);
break;
}
else
{
ret |= ((n & 0x7f) << offset);
}
}
return ret;
}
整个过程就和压缩的时候是逆向的:对于每一个字节,先看最高一位是否有1(0x80)。如果有,就说明不是最后一个数据字节包,那取这个字节的最后七位进行拼装。否则,说明就是已经到了最后一个字节了,那直接拼装后,跳出循环,算法结束。最终得到4字节的整数。
4、总结
好了,整个算法就是差不多几十行,我们却用了几千字来描述他,这就是这个算法精妙的地方。
这个算法使用的基础就是认为在大多数情况下,我们使用的数字都是不大的数字,比如:book_id、comment_count等这种从几到几千数值的东东。那我们也能通过计算,得到每超过一个7位的信息以后,传输的字节数就会增加1。以至于,如果数字比较大的时候,原来4字节的数字还会变成5字节:

不过,在绝大多数情况下,小整数还是占主导的,所以整个算法才有了使用的基础。
好了,不知道老王有没有把这个算法讲清楚。如果没讲清楚,就来看代码吧(Talk is cheap, Show me the code)。
(注:这个代码是老王自己改写的,自己review了,貌似没有错误。如果大家觉得写的有问题,请指正。)
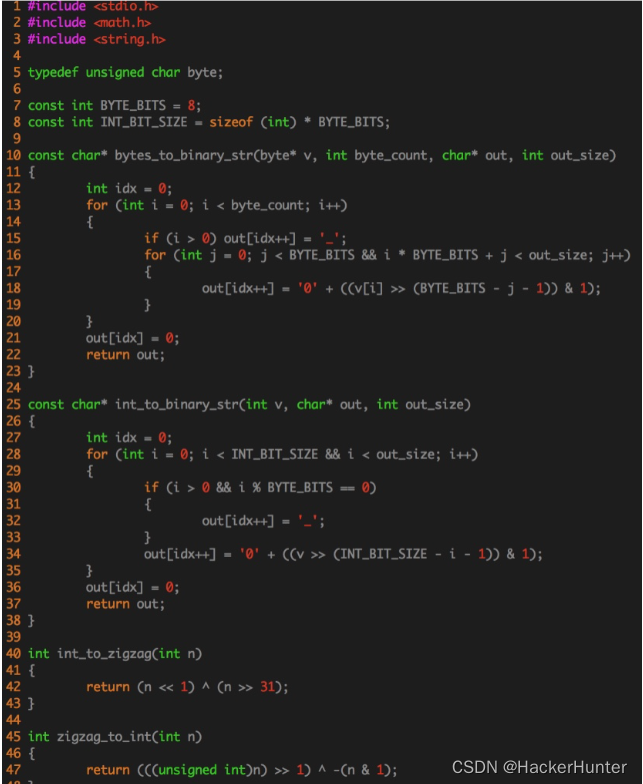
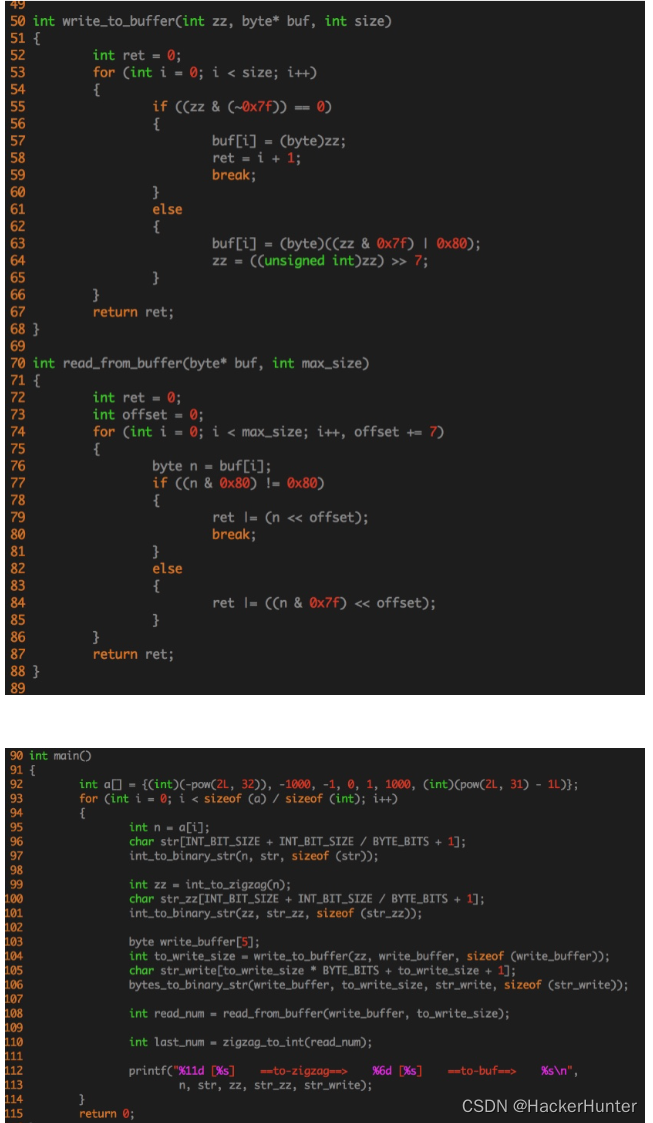
如果觉得c语言代码看起来不是很舒服,也可以去看thrift中java的源代码~
那这一期就聊到这里吧~