题目:491_非递减子序列(看了题解)
给定一个整型数组, 你的任务是找到所有该数组的递增子序列,递增子序列的长度至少是2。
示例:
- 输入: [4, 6, 7, 7]
- 输出: [[4, 6], [4, 7], [4, 6, 7], [4, 6, 7, 7], [6, 7], [6, 7, 7], [7,7], [4,7,7]]
说明:
- 给定数组的长度不会超过15。
- 数组中的整数范围是 [-100,100]。
- 给定数组中可能包含重复数字,相等的数字应该被视为递增的一种情况。
#
算法思想:
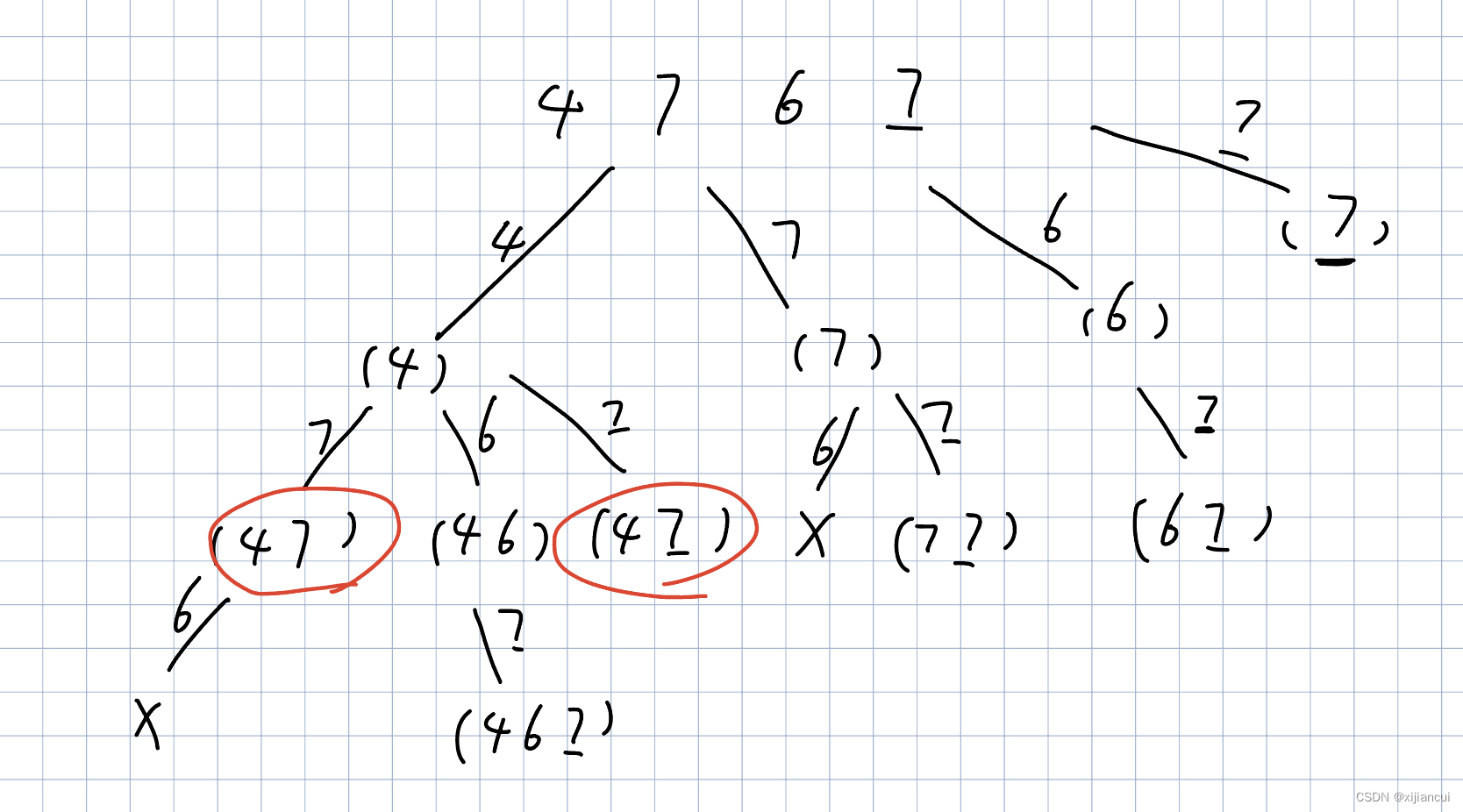
同一层,如果出现了相同元素,则剪掉该分枝,继续该层下一个分枝。
if(path.size()>0&&path.get(path.size()-1)>list.get(i)){
continue;
}
如果当前 元素<path 中最后一个元素,则剪掉该分支,继续该层下一个分枝。
用一个 HashMap 记录每层出现过的元素,在方法体里 new HashMap,每层递归自动创建一个新的 HashMap ,因此不用回溯时退出。
代码:
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
class Solution {
List<Integer> path = new ArrayList();
List<List<Integer>> ans = new ArrayList<>();
public void backtracking(ArrayList<Integer> list ,int startindex){
//递归终止条件
if(startindex>=list.size()){
return;
}
HashMap<Integer,Boolean> map = new HashMap<>(); //map 定义在函数体里,每层递归自动更新一个 map
for (int i = startindex; i <list.size(); i++) {
//树层去重
if(map.containsKey(list.get(i))){
continue;
}
if(path.size()>0&&path.get(path.size()-1)>list.get(i)){
continue;
}
path.add(list.get(i));
if(path.size()>1)
ans.add(new ArrayList<>(path));
map.put(list.get(i),true);
backtracking(list,i+1);
path.remove(path.size()-1);
}
}
public List<List<Integer>> findSubsequences(int[] nums) {
ArrayList<Integer> list = new ArrayList<>();
for (int i = 0; i < nums.length; i++) {
list.add(nums[i]);
}
backtracking(list,0);
return ans;
}
public static void main(String[] args) {
int [] nums = {1,2,3,4,5,6,7,8,9,10,1,1,1,1,1};
System.out.println(new Solution().findSubsequences(nums));
}
}题目:46_全排列(没看题解)
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
示例:
- 输入: [1,2,3]
- 输出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]
#
算法思想:
注意这题是全排列,有序,不用 startindex。
退出递归的条件为 path.size()==list.size();
代码:
import java.util.ArrayList;
import java.util.List;
class Solution {
List<Integer> path = new ArrayList<>();
List<List<Integer>> ans = new ArrayList<>();
void backtracking(ArrayList<Integer> list) {
if (path.size() == list.size()) {
ans.add(new ArrayList<>(path));
return;
}
for (int i = 0; i < list.size(); i++) {
// 树层剪枝
if (path.contains(list.get(i))) {
continue;
}
path.add(list.get(i));
backtracking(list);
path.remove(path.size() - 1);
}
}
public List<List<Integer>> permute(int[] nums) {
ArrayList<Integer> list = new ArrayList<>();
for (int i = 0; i < nums.length; i++) {
list.add(nums[i]);
}
backtracking(list);
return ans;
}
}题目:47_全排列2
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
- 输入:nums = [1,1,2]
- 输出: [[1,1,2], [1,2,1], [2,1,1]]
示例 2:
- 输入:nums = [1,2,3]
- 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
提示:
- 1 <= nums.length <= 8
- -10 <= nums[i] <= 10
#
算法思想:

因为有序,所以不要 startindex;
树层元素要去重,如操作了1,就要剪掉同层 1’;
但树枝不去重,如 {1, 1‘,2} 是合法结果;
用used[] ,标记是同层结点还是同枝结点。同枝则访问过的used 为true,同层因为回溯,访问过的为 false;
代码:
import java.util.ArrayList;
import java.util.Arrays;
import java.util.HashSet;
import java.util.List;
class Solution {
List<Integer> path = new ArrayList<>();
List<List<Integer>> ans = new ArrayList<>();
boolean[] used = new boolean[10]; //用于区分树枝和树层
void backtracking(ArrayList<Integer> list) {
if (path.size() == list.size()) {
ans.add(new ArrayList<>(path));
return;
}
for (int i = 0; i < list.size(); i++) {
// 树层剪枝
if(i>0&&used[i-1]==false&&list.get(i-1)==list.get(i)){
continue;
}
//树枝上,避免取到取过的元素,相当于代替 startindex 的功能
if(used[i]==true)
continue;
used[i] = true;
path.add(list.get(i));
backtracking(list);
path.remove(path.size() - 1);
used[i] = false;
}
}
public List<List<Integer>> permuteUnique(int[] nums) {
Arrays.sort(nums);
ArrayList<Integer> list = new ArrayList<>();
for (int i = 0; i < nums.length; i++) {
list.add(nums[i]);
}
backtracking(list);
return ans;
}
public static void main(String[] args) {
int nums[]={1,1,2};
System.out.println(new Solution().permuteUnique(nums));
}
}